| 编辑推荐: |
本文主要介绍了一套边缘检测的理论,分阶段的解释如何实现边缘检测,希望对您的学习有所帮助。
本文来自于简书,由火龙果软件Alice编辑,推荐。 |
|
Canny 边缘检测算法由计算机科学家 John F. Canny
于 1986 年提出的。其不仅提供了算法,还带来了一套边缘检测的理论,分阶段的解释如何实现边缘检测。Canny
检测算法包含下面几个阶段:
1.灰度化
2.高斯模糊
3.计算图片梯度幅值
4.非极大值抑制
5.双阈值选取
灰度化
灰度化实际上是一种降维的操作,可以减少计算。如果算法不进行色彩相关的识别的话,不灰度化,也可以直接进行后面的阶段。
# 灰度化
def gray(self, img_path):
"""
计算公式:
Gray(i,j) = [R(i,j) + G(i,j) + B(i,j)] / 3
or :
Gray(i,j) = 0.299 * R(i,j) + 0.587 * G(i,j) +
0.114 * B(i,j)
"""
# 读取图片
img = plt.imread(img_path)
# BGR 转换成 RGB 格式
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
# 灰度化
img_gray = np.dot(img_rgb[...,:3], [0.299, 0.587,
0.114])
return img_gray |
高斯模糊
在实际的图片中,都会包含噪声。但有时候,图片中的噪声会导致图片中边缘信息的消失。对此的解决方案就是使用高斯平滑来减少噪声,即进行高斯模糊操作。该操作是一种滤波操作,与高斯分布有关,下面是一个二维的高斯函数,其中
(x, y) 为坐标,σ 为标准差:

进行高斯滤波之前,需要先得到一个高斯滤波器(kernel)。如何得到一个高斯滤波器?其实就是将高斯函数离散化,将滤波器中对应的横纵坐标索引代入高斯函数,即可得到对应的值。不同尺寸的滤波器,得到的值也不同,下面是
(2k+1)x(2k+1) 滤波器的计算公式 :
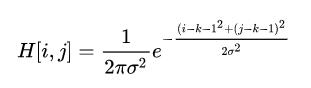
常用尺寸为 5x5,σ=1.4 的高斯滤波器。下面是 5x5 高斯滤波器的实现代码:
# 去除噪音 - 使用 5x5
的高斯滤波器
def smooth(self, img_gray):
# 生成高斯滤波器
"""
要生成一个 (2k+1)x(2k+1) 的高斯滤波器,滤波器的各个元素计算公式如下:
H[i, j] = (1/(2*pi*sigma**2))*exp(-1/2*sigma**2((i-k-1)**2
+ (j-k-1)**2))
"""
sigma1 = sigma2 = 1.4
gau_sum = 0
gaussian = np.zeros([5, 5])
for i in range(5):
for j in range(5):
gaussian[i, j] = math.exp((-1/(2*sigma1*sigma2))*(np.square(i-3)
+ np.square(j-3)))/(2*math.pi*sigma1*sigma2)
gau_sum = gau_sum + gaussian[i, j]
# 归一化处理
gaussian = gaussian / gau_sum
# 高斯滤波
W, H = img_gray.shape
new_gray = np.zeros([W-5, H-5])
for i in range(W-5):
for j in range(H-5):
new_gray[i, j] = np.sum(img_gray[i:i+5, j:j+5]
* gaussian)
return new_gray |
图片梯度幅值
边缘是图像强度快速变化的地方,可以通过图像梯度幅值,即计算图像强度的一阶导数来识别这些地方。由于图片是离散的,可以用有限导数来近似图片的梯度:

图片梯度幅值为:
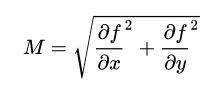
梯度方向为:
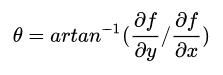
实现代码如下:
# 计算梯度幅值
def gradients(self, new_gray):
"""
:type: image which after smooth
:rtype:
dx: gradient in the x direction
dy: gradient in the y direction
M: gradient magnitude
theta: gradient direction
"""
W, H = new_gray.shape
dx = np.zeros([W-1, H-1])
dy = np.zeros([W-1, H-1])
M = np.zeros([W-1, H-1])
theta = np.zeros([W-1, H-1])
for i in range(W-1):
for j in range(H-1):
dx[i, j] = new_gray[i+1, j] - new_gray[i, j]
dy[i, j] = new_gray[i, j+1] - new_gray[i, j]
# 图像梯度幅值作为图像强度值
M[i, j] = np.sqrt(np.square(dx[i, j]) + np.square(dy[i,
j]))
# 计算 θ - artan(dx/dy)
theta[i, j] = math.atan(dx[i, j] / (dy[i, j] +
0.000000001))
return dx, dy, M, theta |
非极大值抑制(NMS)
理想情况下,最终得到的边缘应该是很细的。因此,需要执行非极大值抑制以使边缘变细。原理很简单:遍历梯度矩阵上的所有点,并保留边缘方向上具有极大值的像素。
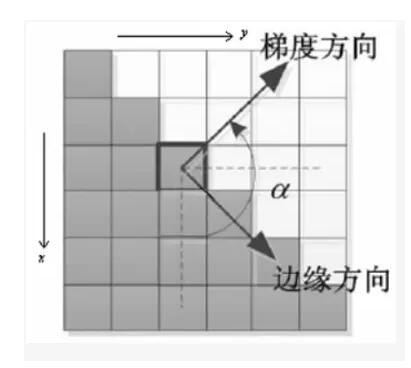
梯度方向与边缘方向相互垂直
下面说说 NMS 的细节内容。NMS 在 4 个方向上进行,分别是
0,90,45,135,没有角度包含两个领域,因此,一共用八个领域:上,下,左,右,左上,左下,右上,右下,如下图所示,C
周围的 8 个点就是其附近的八个领域。
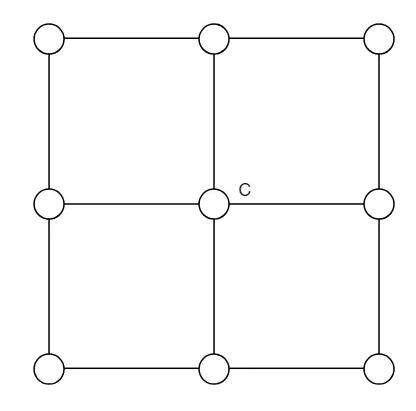
这样做的好处是简单, 但是这种简化的方法无法达到最好的效果, 因为,自然图像中的边缘梯度方向不一定是沿着这四个方向的。因此,就有很大的必要进行插值,找出在一个像素点上最能吻合其所在梯度方向的两侧的像素值。
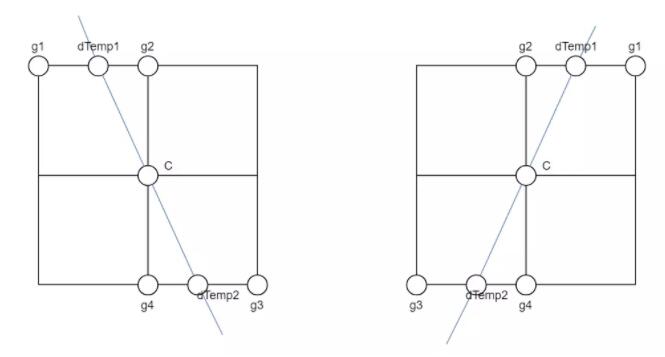
NMS 是要找出局部最大值,因此,需要将当前的像素的梯度,与其他方向进行比较。如下图所示,g1,g2,g3,g4
分别是 C 八个领域中的 4 个点,蓝线是 C 的梯度方向。如果 C 是局部最大值的话,C 点的梯度幅值就要大于梯度方向直线与
g1g2,g4g3 两个交点的梯度幅值,即大于点 dTemp1 和 dTemp2 的梯度幅值。上面提到这种方法无法达到最好的效果,因为
dTemp1 和 dTemp2 不是整像素,而是亚像素。亚像素的意思就是在两个物理像素之间还有像素。
那么,亚像素的梯度幅值怎么求?可以使用线性插值的方法,计算 dTemp1 在 g1,g2 之间的权重,就可以得到其梯度幅值。计算公式如下:
weight = |gx|
/ |gy| or |gy| / |gx|
dTemp1 = weight*g1 + (1-weight)*g2
dTemp2 = weight*g3 + (1-weight)*g4 |
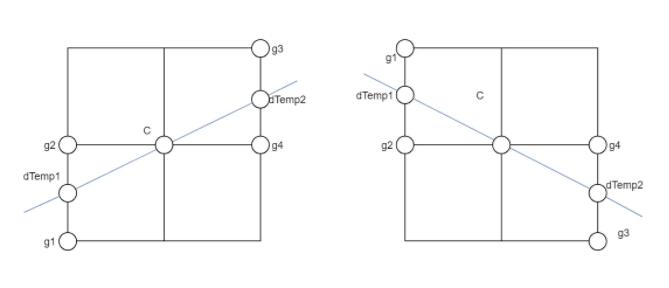
下面两幅图是 y 方向梯度值比较大的情况,即梯度方向靠近 y 轴。所以,g2
和 g4 在 C 的上下位置,此时 weight = |gy| / |gx| 。左边的图是 x,y
方向梯度符号相同的情况,右边是 x,y 方向梯度符号相反的情况。
对于左边的图来说,以 C 点为当前位置 - d[i, j] ,那么
g2 在 C 的前一行,g4 在 C 的后一行,所以位置坐标是:<br />g2 = d[i-1,
j];g4 = d[i+1, j]。根据左图的位置关系可以得到:g1 = d[i-1, j-1];g3
= d[i+1, j+1]。
同理,根据右图的位置关系可以得到:g1 = d[i-1, j+1];g3 = d[i+1, j-1]。
下面两幅图是 x 方向梯度值比较大的情况,即梯度方向靠近 x 轴。所以,g2
和 g4 在 C 的左右位置,此时 weight = |gy| / |gx| 。左边的图是 x,y
方向梯度符号相同的情况,右边是 x,y 方向梯度符号相反的情况。
由上面可知,可以得到如下信息:g2 = d[i, j-1];g4 =
d[i, j+1];
左图:g1 = d[i+1, j-1];g3 = d[i-1, j+1];
右图:g1 = d[i-1, j-1];g3 = d[i+1, j+1]。
下面的这两幅图,可能会带来理解帮助:
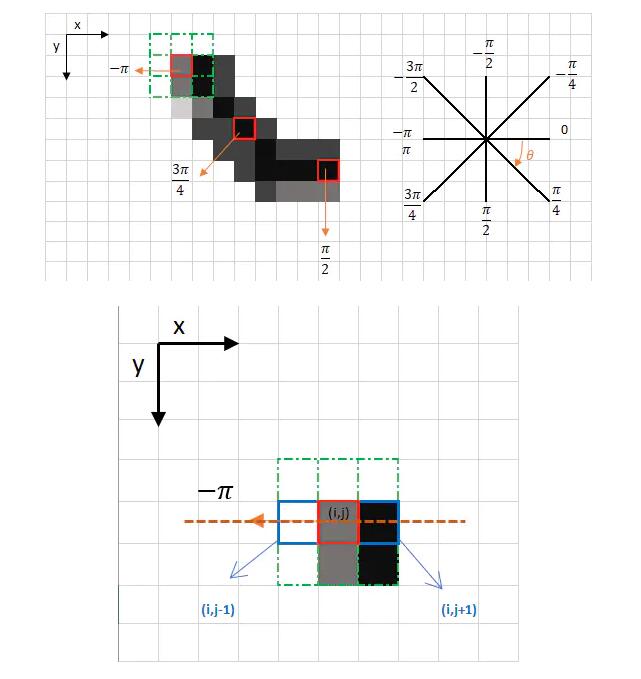
然后,根据以上信息,代码实现如下:
def NMS(self,
M, dx, dy):
d = np.copy(M)
W, H = M.shape
NMS = np.copy(d)
NMS[0, :] = NMS[W-1, :] = NMS[:, 0] = NMS[:, H-1]
= 0
for i in range(1, W-1):
for j in range(1, H-1):
# 如果当前梯度为0,该点就不是边缘点
if M[i, j] == 0:
NMS[i, j] = 0
else:
gradX = dx[i, j] # 当前点 x 方向导数
gradY = dy[i, j] # 当前点 y 方向导数
gradTemp = d[i, j] # 当前梯度点
# 如果 y 方向梯度值比较大,说明导数方向趋向于 y 分量
if np.abs(gradY) > np.abs(gradX):
weight = np.abs(gradX) / np.abs(gradY) # 权重
grad2 = d[i-1, j]
grad4 = d[i+1, j]
# 如果 x, y 方向导数符号一致
# 像素点位置关系
# g1 g2
# c
# g4 g3
if gradX * gradY > 0:
grad1 = d[i-1, j-1]
grad3 = d[i+1, j+1]
# 如果 x,y 方向导数符号相反
# 像素点位置关系
# g2 g1
# c
# g3 g4
else:
grad1 = d[i-1, j+1]
grad3 = d[i+1, j-1]
# 如果 x 方向梯度值比较大
else:
weight = np.abs(gradY) / np.abs(gradX)
grad2 = d[i, j-1]
grad4 = d[i, j+1]
# 如果 x, y 方向导数符号一致
# 像素点位置关系
# g3
# g2 c g4
# g1
if gradX * gradY > 0:
grad1 = d[i+1, j-1]
grad3 = d[i-1, j+1]
# 如果 x,y 方向导数符号相反
# 像素点位置关系
# g1
# g2 c g4
# g3
else:
grad1 = d[i-1, j-1]
grad3 = d[i+1, j+1]
# 利用 grad1-grad4 对梯度进行插值
gradTemp1 = weight * grad1 + (1 - weight) *
grad2
gradTemp2 = weight * grad3 + (1 - weight) *
grad4
# 当前像素的梯度是局部的最大值,可能是边缘点
if gradTemp >= gradTemp1 and gradTemp >=
gradTemp2:
NMS[i, j] = gradTemp
else:
# 不可能是边缘点
NMS[i, j] = 0
return NMS |
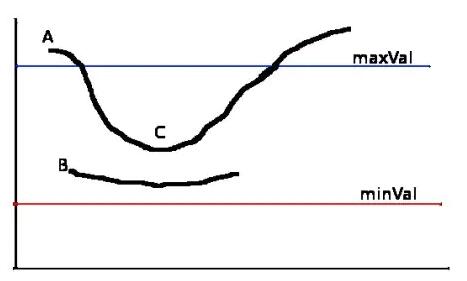
双阈值选取
这个阶段决定哪些边缘是真正的边缘,哪些边缘不是真正的边缘。为此,需要设置两个阈值,minVal
和 maxVal。梯度大于 maxVal 的任何边缘肯定是真边缘,而 minVal 以下的边缘肯定是非边缘,因此被丢弃。位于这两个阈值之间的边缘会基于其连通性而分类为边缘或非边缘,如果它们连接到“可靠边缘”像素,则它们被视为边缘的一部分。否则,也会被丢弃。
代码如下所示:
def double_threshold(self,
NMS):
W, H = NMS.shape
DT = np.zeros([W, H])
# 定义高低阈值
TL = 0.1 * np.max(NMS)
TH = 0.3 * np.max(NMS)
for i in range(1, W-1):
for j in range(1, H-1):
# 双阈值选取
if (NMS[i, j] < TL):
DT[i, j] = 0
elif (NMS[i, j] > TH):
DT[i, j] = 1
# 连接
elif (NMS[i-1, j-1:j+1] < TH).any() or (NMS[i+1,
j-1:j+1].any()
or (NMS[i, [j-1, j+1]] < TH).any()):
DT[i, j] = 1
return DT |
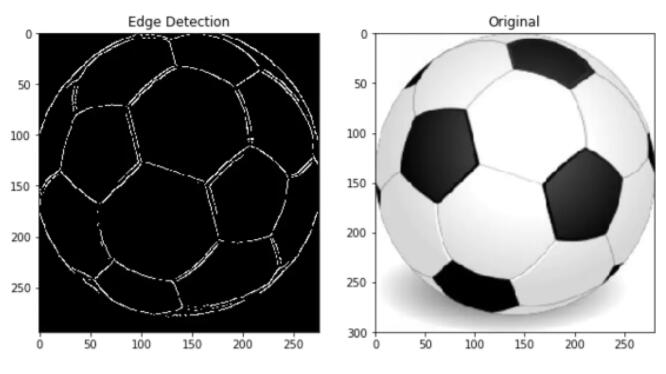
边缘检测结果
经过以上 5 个过程,可以得到如下结果:
将其与 OpenCV,skimage 算法进行对比:
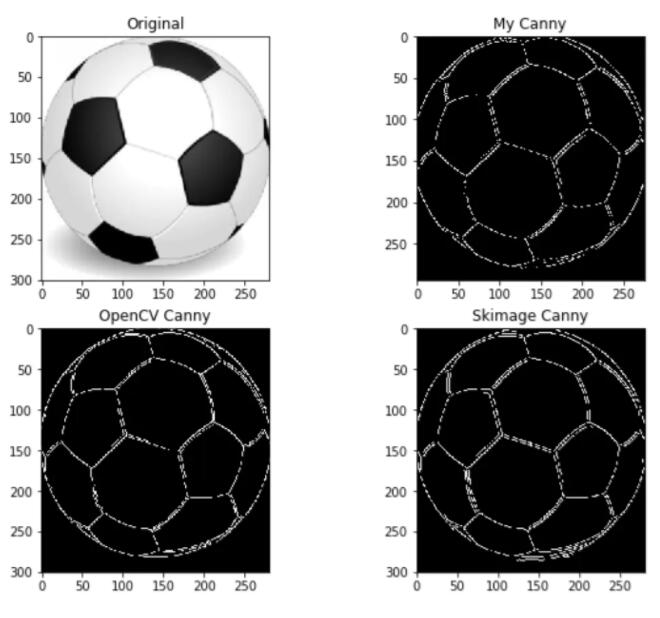
我个人感觉 OpenCV 的结果是最好的,其次是 Skimage 的结果。自己的算法结果有些地方还是蛮粗糙的。
|