| 编辑推荐: |
本文讲了对数坐标图,极坐标图像,柱状图,散列图,由离散的点构成的,3D图像,主要是调用3D图像库,希望对大家有帮助。
本文来自于csdn,由火龙果软件Delores编辑,推荐。 |
|
首先补充一下:两种体系7种颜色 r g b y m c k (红,绿,蓝,黄,品红,青,黑)
在科研的过程中,坐标系中的XY不一定就是等尺度的。例如在声波中对Y轴取对数。肆意我们也必须知道这种坐标系如何画出来的。
1:对数坐标图
有3个函数可以实现这种功能,分别是:semilogx(),semilogy(),loglog()。它们分别表示对X轴,Y轴,XY轴取对数。下面在一个2*2的figure里面来比较这四个子图(还有plot())。
def drawsemilogx():
w=np.linspace(0.1,1000,1000)
p=np.abs(1/(1+0.1j*w))
plt.subplot(221)
plt.plot(w,p,lw=2)
plt.xlabel('X')
plt.ylabel('y');
plt.subplot(222)
plt.semilogx(w,p,lw=2)
plt.ylim(0,1.5)
plt.xlabel('log(X)')
plt.ylabel('y')
plt.subplot(223)
plt.semilogy(w,p,lw=2)
plt.ylim(0,1.5)
plt.xlabel('x')
plt.xlabel('log(y)')
plt.subplot(224)
plt.loglog(w,p,lw=2)
plt.ylim(0,1.5)
plt.xlabel('log(x)')
plt.xlabel('log(y)')
plt.show() |
如上面的代码所示,对一个低通滤波器函数绘图。得到四个不同坐标尺度的图像。如下图所示
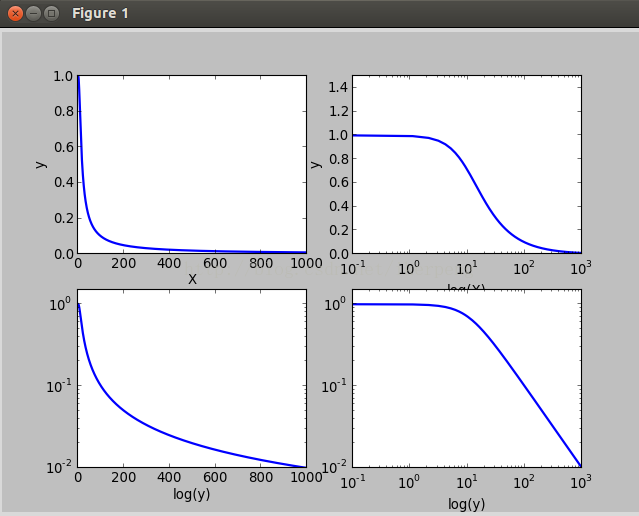
2,极坐标图像
极坐标系中的点由一个夹角和一段相对于中心位置的距离来表示。其实在plot()函数里面本来就有一个polar的属性,让他为True就行了。下面绘制一个极坐标图像:
def drawEightFlower():
theta=np.arange(0,2*np.pi,0.02)
plt.subplot(121,polar=True)
plt.plot(theta,2*np.ones_like(theta),lw=2)
plt.plot(theta,theta/6,'--',lw=2)
plt.subplot(122,polar=True)
plt.plot(theta,np.cos(5*theta),'--',lw=2)
plt.plot(theta,2*np.cos(4*theta),lw=2)
plt.rgrids(np.arange(0.5,2,0.5),angle=45)
plt.thetagrids([0,45,90]);
plt.show(); |
整个代码很好理解,在后面的13,14行没见过。第一个plt.rgrids(np.arange(0.5,2,0.5),angle=45) 表示绘制半径为0.5 1.0 1.5的三个同心圆,同时将这些半径的值标记在45度位置的那个直径上面。plt.thetagrids([0,45,90]) 表示的是在theta为0,45,90度的位置上标记上度数。得到的图像是:
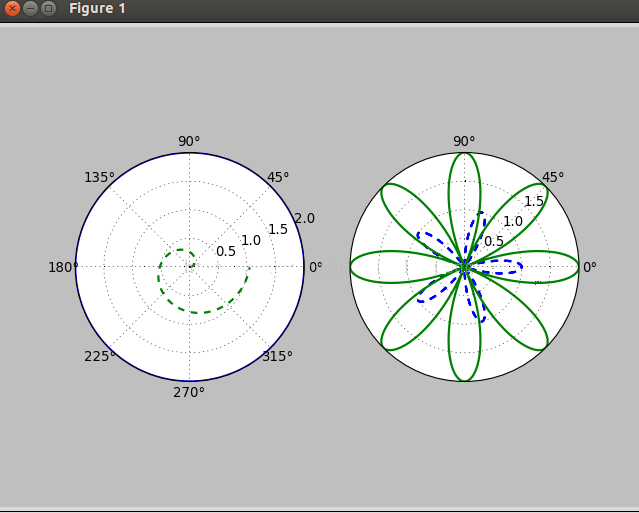
3,柱状图:
核心代码matplotlib.pyplot.bar(left, height, width=0.8, bottom=None, hold=None, **kwargs)里面重要的参数是左边起点,高度,宽度。下面例子:
def drawPillar():
n_groups = 5;
means_men = (20, 35, 30, 35, 27)
means_women = (25, 32, 34, 20, 25)
fig, ax = plt.subplots()
index = np.arange(n_groups)
bar_width = 0.35
opacity = 0.4
rects1 = plt.bar(index, means_men,
bar_width,alpha=opacity,
color='b',label= 'Men')
rects2 = plt.bar(index + bar_width,
means_women,
bar_width,alpha=opacity,
color='r',
label='Women')
plt.xlabel('Group')
plt.ylabel('Scores')
plt.title('Scores by group and gender')
plt.xticks(index + bar_width,
('A', 'B', 'C',
'D', 'E'))
plt.ylim(0,40);
plt.legend();
plt.tight_layout();
plt.show(); |
得到的图像是:
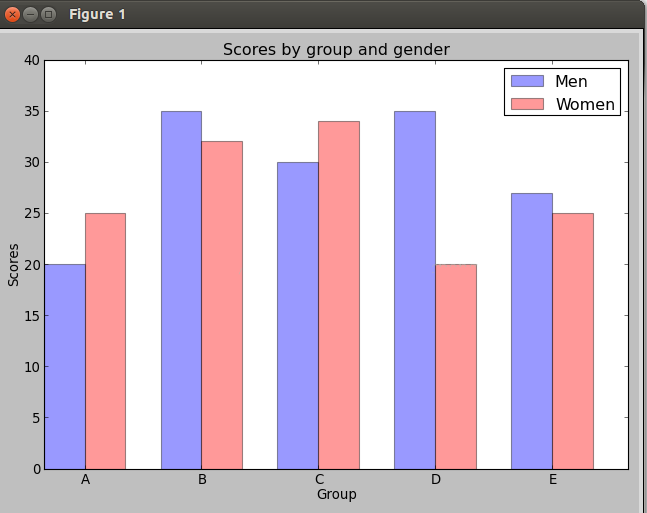
再贴一图:
这是我关于pose识别率的实验结果,感觉结果真是令人不可思议
def drawBarChartPoseRatio():
n_groups = 5
means_VotexF36 = (0.84472049689441,
0.972477064220183,
1.0, 0.9655172413793104,
0.970970970970971)
means_VotexF50 = (1.0, 0.992992992992993,
1.0,
0.9992348890589136, 0.9717125382262997)
means_VFH36 = (0.70853858784893,
0.569731081926204,
0.8902900378310215,
0.8638638638638638, 0.5803008248423096)
means_VFH50 = (0.90786948176583,
0.796122576610381,
0.8475120385232745,
0.8873762376237624, 0.5803008248423096)
fig, ax = plt.subplots()
index = np.arange(n_groups)
bar_width = 0.3
opacity = 0.4
rects1 = plt.bar(index, means_VFH36,
bar_width/2,
alpha=opacity, color='r',
label='VFH36' )
rects2 = plt.bar(index+ bar_width/2,
means_VFH50,
bar_width/2, alpha=opacity,
color='g', label='VFH50'
)
rects3 = plt.bar(index+bar_width,
means_VotexF36,
bar_width/2,
alpha=opacity, color='c', label='VotexF36')
rects4 = plt.bar(index+1.5*bar_width,
means_VotexF50,
bar_width/2, alpha=opacity,
color='m', label='VotexF50')
plt.xlabel('Category')
plt.ylabel('Scores')
plt.title('Scores by group and Category')
#plt.xticks(index - 0.2+ 2*bar_width,
('balde',
'bunny', 'dragon', 'happy', 'pillow'))
plt.xticks(index - 0.2+ 2*bar_width,
('balde',
'bunny', 'dragon', 'happy', 'pillow'),
fontsize
=18)
plt.yticks(fontsize =18) #change the num axis
size
plt.ylim(0,1.5) #The ceil
plt.legend()
plt.tight_layout()
plt.show()
|
柱状图显示:
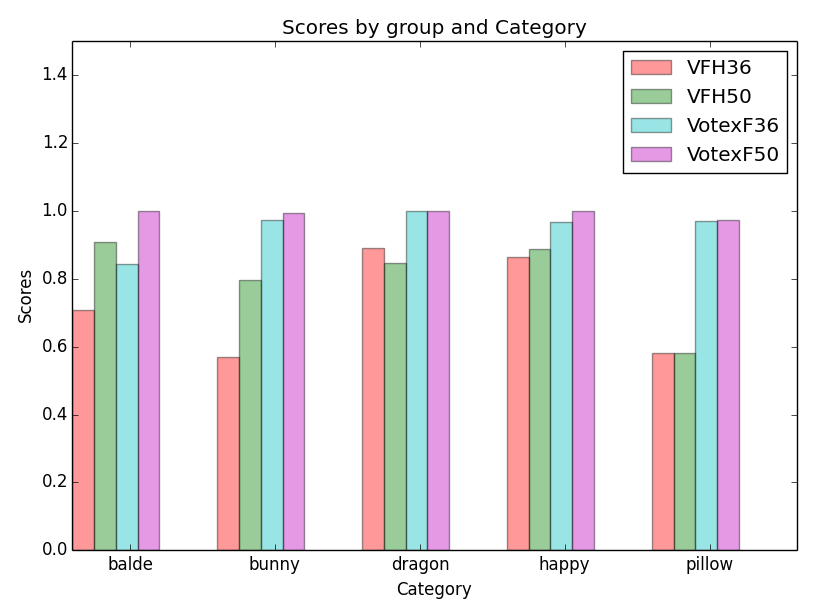
4:散列图,由离散的点构成的。
函数是:
matplotlib.pyplot.scatter(x, y, s=20, c='b', marker='o', cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, verts=None, hold=None,**kwargs),其中,xy是点的坐标,s点的大小,maker是形状可以maker=(5,1)5表示形状是5边型,1表示是星型(0表示多边形,2放射型,3圆形);alpha表示透明度;facecolor=‘none’表示不填充。例子如下:
def drawStar():
plt.figure(figsize=(8,4))
x=np.random.random(100)
y=np.random.random(100)
plt.scatter(x,y,s=x*1000,c='y',marker=(5,1),
alpha=0.5,lw=2,facecolors='none')
plt.xlim(0,1)
plt.ylim(0,1)
plt.show() |
上面代码的facecolors参数使得前面的c=‘y’不起作用了。图像:
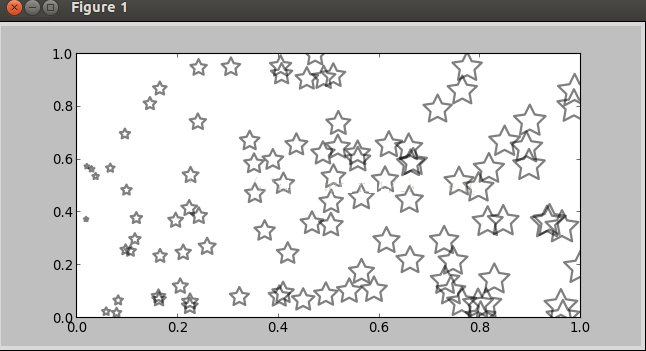
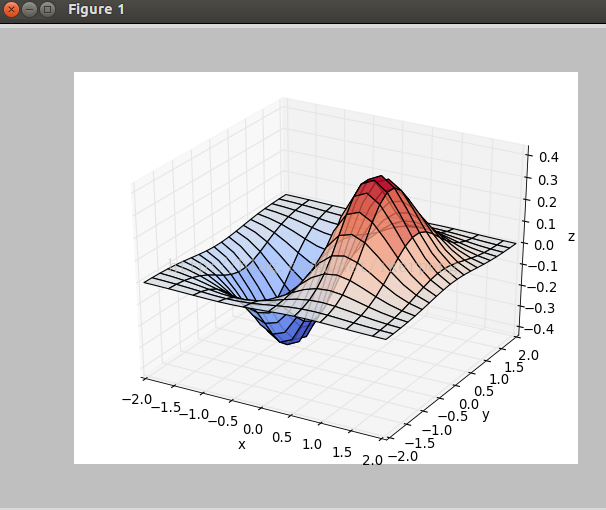
5,3D图像,主要是调用3D图像库。看下面的例子:
def draw3Dgrid():
x,y=np.mgrid[-2:2:20j,-2:2:20j]
z=x*np.exp(-x**2-y**2)
ax=plt.subplot(111,projection='3d')
ax.plot_surface(x,y,z,rstride=2,cstride=1,
cmap=plt.cm.coolwarm,alpha=0.8)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show() |
得到的图像如下图所示:
到此,matplotlib基本操作的学习结束了,相信大家也可以基本完成自己的科研任务了。
|