| 编辑推荐: |
| 本文来自于CSDN,主要讲了数据结构算法及python,其中有Stack, Queue、链表和多重数组、散列表、二叉查找树、红黑树、图的表示和搜索。 |
|
Stack, Queue
Stack是后进先出, LIFO, 队列为先进先出, FIFO
在python中两者, 都可以简单的用list实现,
进, 用append()
出, Stack用pop(), Queue用pop(0), pop的时候注意判断len(l)
对于优先队列, 要用到前面讲到的堆
链表和多重数组
这些数据结构在python中就没有存在的价值, 用list都能轻松实现
散列表
为了满足实时查询的需求而产生的数据结构, 查询复杂度的期望是O(1), 最差为O(n)
问题描述, 对于n个(key, value)对, 怎样存储可以在O(1)的时间复杂度内获取特定key所对应的value. 这个问题里, key默认是int, 当然key可以是字符串或其他, 那就想办法把key转换成int.
最简单的方法是直接寻址表 , 就是创建和key空间一样大小的数组A, 把value存储到数组A[key]中.
这个方法简单, 对应key空间不大的情况也可以用, 但是当key空间很大时, 这个太耗内存了, 而且没有必要, 比如只有10个范围在1到1000000的key, 你要分配个那么大的数组, 明显不合适
散列方法 , 自然想到我们应该用一个较小的数组来存储, 那么就需要把key空间范围中的数字映射到较小所存储空间上来. 这个映射的方法, 称为散列函数 . 散列函数的选择是很关键的, 而且这个没有绝对的好坏, 每个散列函数都有它的适用范围.
常用的散列函数如下, 将关键字k映射到m个槽
除法散列法, h(k) = k mod m
乘法散列法, h(k) = |m(KA mod 1)|, 0 全域散列, 想法就是准备一组散列函数, 每次使用时随机选择一个, 来克服散列函数的局限性. 比如定义散列函数组,h(k) = ((ak+b) mod p)mod m, p是足够大的质数, 随机选择不同的a,b产生不同的散列函数
那么把一个大的数字空间映射到一个较小的数字空间上, 那么肯定会有重复, 这是不可避免的, 这种重复称为碰撞 (collision).
有碰撞就要想办法解决, 最简单的想法, 就是链接法 .
理想状态每个槽里面只放一个key, 那么search肯定是O(1)的, 直接就找到. 但是重复是不可避免, 如果有多个key被分配到同一个槽, 怎么办
那么在槽中存放一个key的链表来存储多个key, 这样search肯定大于O(1), 最差的情况为O(n). 平均为O(1+a), a为装载因子(load factor), 一个槽中平均存储的元素数.
所以我们应该尽量减少碰撞的可能性, 最直接的方法是减少装载因子
另一种解决碰撞的方法就是开放寻址法 , 做法是出现碰撞时, 根据规则探测另一个槽存放该元素
这个方法的好处就是没有用链表, 不用指针, 节省的空间可以提供更多的槽, 坏处是数据可能会溢出, 所以要确保装载因子不能大于1
现在的问题就是当发生碰撞时, 怎么样去探测下一个槽
线性探测, h(k,i)=(h'(k)+i) mod m,i=0,1,……,m-1, 这个方法会有个问题, 一次集群, 连续被占用的槽会不断增加, 那么后面侦测的时间会变长
二次探测, h(k,i)=(h'(k)+c1*i+c2*i2 ) mod m, 这样不用一个个连续去探测, 因为有个平方, 会隔的远些, 但还是会有二次集群, 因为初始探测决定了整个探测序列
双重哈希 , h(k,i)=(h1(k)+i*h2(k)) mod m, 这时现在最好的探测方法
开放寻址法search复杂度为O(1/(1-a)), a为装载因子
止于至善, 有没有一种方法可以在最差情况下也能达到O(1), 理论上是有的, 但必须是输入数据为静态数据, 方法叫perfect hashing, 完美散列
思路也不复杂, 采用两级hash, 一级类似于链接法, 采用全域散列把n个输入划分到m个槽内, 然后在每个槽内进行二级散列, 并确保二级散列是无冲突的.
可以证明当, m = n2 时, 出现冲突的概率小于0.5, 所以只要保证一级散列函数选取合适, 可以均匀的把n个元素分布到m个槽中, 并保证槽中二级散列的空间足够大, 就可以达到效果.
在python中, 无需自己实现散列表, 用dict就可以
二叉查找树
二叉查找树, 也是一种便于查找的数据结构, 任意一个树节点的左子树都小于该节点, 右子树都大于该节点. 随机构造的二叉树, 理想树高为logn, 其上操作的平均复杂度为O(logn)
既然前面的Hash可以提供O(1)的search, 为什么还需要这个数据结构了, 他更灵活, 他可以提供除search外的其他操作, 如Minimum, Maximum, Predecessor, Successor, Insert等操作.
他可以用于字典, 或优先队列, 可是如果字典, 我首选Hash, 优先队列, 我首选堆, 没有想到非要用二叉树的例子, 往往是二叉树的变种更有实用价值.
二叉树最大的问题, 是构造顺序不能保证是随机的, 就是说不能保证二叉树是平衡的, 不平衡就麻烦了, 极限情况是个单链表. 常用的一种平衡二叉树, 为红黑树.
B树也是二叉树很有用的变种, 常用于创建数据库索引, 后面会具体讨论.
下面给出python实现
1 class Node:
2
3 def __init__(self,data):
4 self.left = None
5 self.right = None
6 self.parent = None
7 self.data = data
8
9 def insert(self, data):
10 # #recursion version
11 # if data < self.data:
12 # if self.left:
13 # self.left.insert(data)
14 # else:
15 # self.left = self.createNode(data)
16 # self.left.parent = self
17 # else:
18 # if self.right:
19 # self.right.insert(data)
20 # else:
21 # self.right = self.createNode(data)
22 # self.right.parent = self
23 #non-recursion version
24 node = self
25 while node:
26 if data < node.data:
27 next = node.left
28 else:
29 next = node.right
30 if next:
31 node = next
32 else:
33 break
34 nn = self.createNode(data)
35 if data < node.data:
36 node.left = nn
37 node.left.parent = node
38 else:
39 node.right = nn
40 node.right.parent = node
41 return nn
42
43 def createNode(self, data):
44 return Node(data)
45
46 def printTree (self):
47 """中序遍历"""
48 if self.left:
49 self.left.printTree()
50 print self.data
51 if self.right:
52 self.right.printTree()
53
54 def maxNode(self):
55 if self.right:
56 return self.right.maxNode()
57 else:
58 return self
59
60 def minNode (self):
61 if self.left:
62 return self.left.maxNode()
63 else:
64 return self
65
66 def lookup(self, data):
67 if self.data == data:
68 return self
69
70 if self.data > data:
71 if self.left:
72 return self.left.lookup(data)
73 else:
74 return None
75 else:
76 if self.right:
77 return self.right.lookup(data)
78 else:
79 return None
80
81 def successor(self):
82 """
83 有右子树时,很容易理解, 取右子树的最小值
84 没有右子树时, 也就是说该节点是当前子树的最大节点, 该节点的后继为把该子树作为左子树的最近的根节点
85 如果要取前驱, 道理一样
86 """
87 n= self
88 if n.right:
89 return n.right.minNode()
90 else:
91 p = n.parent
92 while p and p.right == n:
93 n = p
94 p = p.parent
95 return p
96
97 def delete(self, root):
98 """
99 对于没有子树,或只有一个子树, 都很好处理
100 如果有两个子树, 做法是把节点后继节点拷贝到当前节点, 然后删除后继节点
101 这不是唯一的做法, 但这样做对树原有的平衡性破坏最小
102 当root被删除时, root会变, 所以需要返回新的root
103 """
104 n= self
105
106 if n.left and n.right:
107 s = n.right.minNode()
108 n.data = s.data
109 root = s.delete(root)
110 return root
111
112 #特殊处理根节点
113 if not n.parent:
114 if n.left:
115 root = n.left
116 n.left = None
117 root.parent = None
118 elif n.right:
119 root = n.right
120 n.right = None
121 root.parent = None
122 else:
123 root = None
124
125 return root
126
127 if not n.left and not n.right:
128 if n.parent.left == n:
129 n.parent.left = None
130 else:
131 n.parent.right = None
132 else:
133 if n.parent.left == n:
134 n.parent.left = n.left or n.right
135 else:
136 n.parent.right = n.left or n.right
137 n.parent = None
138 return root
139 def buildTree():
140 root = Node(8)
141 root.insert(3)
142 root.insert(10)
143 root.insert(1)
144 root.insert(6)
145 root.insert(4)
146 root.insert(7)
147 root.insert(14)
148 root.insert(13)
149 root.printTree() |
红黑树
前面说了, 二叉查找树最大的问题就是平衡性, 而红黑树就很好的解决了这个问题, 什么是红黑树
1)每个结点要么是红的,要么是黑的。
2)根结点是黑的。
3)每个叶结点,即空结点(NIL)是黑的。
4)如果一个结点是红的,那么它的俩个儿子都是黑的。
5)对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
满足上面几点就叫做红黑树, 坦白的讲, 这个数据结构真是有够复杂的, 对于能想出这样方法的NB, 崇拜之情如滔滔江水

这个树有什么, 明显就是比较平衡, 因为根到叶的最长距离最多是最短距离的2倍, 为什么
因为黑高(包含的黑节点数)都是一样的, 所以最短路径就是全黑, 最长路径为红黑交替, 所以最长最多是最短2倍.
可以证明红黑树的高度至多为2lg(n+1), 树的操作复杂度完全取决于树高, 这就很好的解决了二叉树的不平衡问题.
红黑树比较有特色的操作为旋转(pivot) ,
红黑树的插入操作
对于红黑树的插入, 默认插入节点为红节点, 必须是红的, 根是黑的, 如果插黑的, 就和二叉树没有区别了. 而且插红的不会打破黑高相同规则5), 只会打破规则2), 4), 所以只需要针对这两个规则进行rebalance. 抛开rebalance不谈, 红黑树的插入操作和二叉树相同的, 但是关键就是插完后的rebalance过程来保证红黑树的规则.
rebalance的过程是比较复杂的, 不过我们可以case by case的分析, 总的来说只有两种操作, 旋转 和变色 , 并且只有出现连续两个黑色节点时才需要旋转.
1) 插入的是根结点,直接把此结点变为黑色
2) 插入的结点的父结点是黑色, 很好什么也不用做
3) 当前结点的父结点是红色且祖父结点的另一个子结点(叔叔结点)是红色
父节点红色, 打破了规则4), 而且可以推断祖父肯定是黑的, 并且叔叔结点是红色, 说明这个子树是平衡的(黑红相间), 不需要旋转.
既然不旋转就变色, 父节点和叔叔节点变黑,祖父结点变红,那这样祖父节点就有可能违反规则, 所以继续对祖父节点进行rebalance
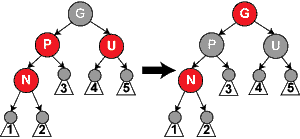
4)当前节点的父节点是红色,叔叔节点是黑色
这种情况比较复杂, 因为祖父肯定是黑的, 叔叔节点也是黑的, 所以出现连续两个黑色节点, 树不平衡, 肯定需要旋转, 怎么个旋转法
首先要看叔叔节点是祖父节点的左节点, 还是右节点, 这个决定了旋转的方向, 我们只需要讨论其中一种情况, 另一种情况就是往相反的方向旋转就可以了
我们就讨论一下叔叔节点是祖父节点的右节点的情况, 就是父节点为祖父节点的左节点, 这儿根据当前节点位置又分为两种情况,
a)当前节点为父节点的右节点, 以父节点左旋, 并把父节点作为当前节点
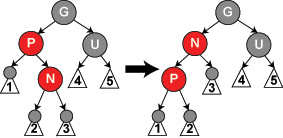
b)当前节点为父节点的左节点, 以祖父节点右旋, 并改变父节点, 祖父节点颜色
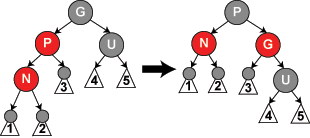
大家想一下, 这种情况下旋转的目的是因为在祖父节点的右子树上连续出现两个黑节点, 所以我们最终需要通过一次右旋来增加右子树的高度, 就如b)情况所示, 通过一次右旋, 并改色, 达到了恢复红黑树的所有规则.
但对于a), 你可以试着直接右旋, 你没法改色来满足红黑树的规则, 所以要先通过一次左旋来达到b), 进而进行右旋, 所以a)只是一个中间步骤.
好了, 这边分析完叔叔节点是祖父节点的右节点的情况, 对于叔叔节点是祖父节点的左节点的情况, 类似想想也能明白.
红黑树的删除操作
回想一下前面二叉树的删除操作, 如果需要删除的节点有两个儿子,那么问题可以被转化成删除另一个只有一个儿子的节点的问题 (这里的儿子,为非叶子节点的儿子,红黑树中leaf节点都是Null节点)。为什么?因为这儿的删除操作过程, 是找到该节点的后继, copy到当前节点, 然后删除后继(右子树中最小节点),此时的后继节点最多只有一个儿子(并且是右儿子),否则就不是后继。
所以问题简化为,我们只需要讨论删除只有一个儿子的节点 (如果它两个儿子都为空,即均为叶子,我们任意将其中一个看作它的儿子),到这儿我们就把一个看似复杂的问题转化为相对简单的问题。
在删除这个节点时,根据颜色不同,分为3种情况,
1)该节点为红色,这种情况一定没有儿子,直接删除没有任何影响
2)该节点为黑色,如果有儿子一定是有且只有一个红色的儿子,这个也好办,把红色的儿子替换改节点, 并改为黑色。
3)该节点为黑色,且没有儿子,即只有两个叶子,这个问题就比较复杂了,你直接删除这个节点, 破坏了规则5),这个分支明显比其他黑高少1.
现在就对上面情况3)具体分析,思路是什么,明显直接从该节点上没法解决问题,他被干掉了,他也没有儿子,那就找他父亲,兄弟吧,总要有人负责的吗, 如果他没有父亲了,孤儿, 他就是根节点, 他被干掉, 树都没了,当然不用做啥了。而且如果有父亲,他就一定有兄弟,不流行只生一个。
那么就把他的父节点,兄弟节点一起考虑进来,形成一个子树来解决这个问题。怎么解决? 那么我就来谈谈我的理解,
攘外必先安内,第一步我们首先保证这个子树内部是满足红黑树规则的(我们假设被删除的节点在左子树, 在右子树一样处理, 只是旋转方向相反)
现在的情况时被删除子树的黑高比他的兄弟子树黑高少1, 怎么办
a)最简单的是, 把兄弟节点改红, 这样让他的黑高也减1
这种改法必须满足的条件是, 兄弟节点首先是黑的, 而且他的子节点也都是黑的(Case 2 ), 这样可以直接把兄弟节点由黑改红, 在不破坏其他规则的前提下, 使两个子树黑高相同.
但是你不能保证这种case一定出现, 其他情况如下,
b)兄弟节点是红的, 这种情况下, 兄弟节点一定是两个黑色子节点(Case1 ). 这种情况下, 通过对父节点的一次左旋并改色, 就能够满足(Case 2)的条件.
c)兄弟节点是黑的, 但兄弟节点的子节点至少有一个是红色的. 这样你也没法直接改兄弟节点的颜色, 改了就和红子节点矛盾了.
c1)如果兄弟节点的右儿子SR 是红色的(Case4 ), 做法是把父节点做一次左旋, 并把父节点和都改成SR 黑色 , 这样左右子树的黑高就相同了.
c2)如果兄弟节点只有左儿子SL 是红色的(Case3 ), 无法直接按c1处理, 因为通过左旋把右子树挪了一个黑节点, 到左子树, 但右子树没有可以改黑的红节点, 导致右子树黑高少1.
所以需要通过对兄弟节点S进行一次右旋, 并改色, 就可以满足(Case 4 )的条件.
第二步, 现在子树内部黑高已经平衡, 但对于整个红黑树而言, 黑高是否平衡
可以看到对于c)而言, 子树内的黑高不增不减, 对全局没有影响
但对于a)b)而言, 为了平衡内部黑高, 子树的黑高整个减少1 (Case 2 )
如果子树的根结点为红, 把它变黑就可以解决这个问题(红黑树中, 节点变黑比较方便只需考虑黑高, 变红比较麻烦)
如果子树根节点为黑, 这就相当于, 把我们刚解决的问题(子树黑高少1), 往上(朝根节点方向)提升了一层, 递归去解决. 如果这个问题一直无法解决, 最终会提升到根节点的位置, 这时这个问题就不用解决了, 相当于把整个红黑树的黑高都减了1, 这样也平衡了.
有了上面的理解再去看Wiki或算法导论具体的算法就比较容易了, 个儿觉得它们对于删除解释的不够清楚, 而且图画的比较让人困惑, 比如你看看(Case1 )的图, 对于左图是删除后的情况, 要转化为右图, 你看看左图有黑高不平衡吗, 明显是平衡的吗, 那还做什么 对于N而言, 要么是叶节点, 要么是一棵子树, 他的黑高应该和3,4,5,6节点(或子树)一致的, 你说这个图画的怪不怪, 误导性很强, 只能大概示意, 不过大家都用这个图, 我也就不改了.
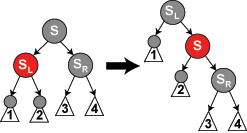
1)兄弟S 是红色。
在这种情况下我们在N的父亲上做左旋转 ,把红色兄弟转换成N的祖父。我们接着对调 N 的父亲和祖父的颜色。
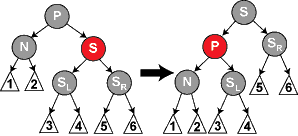
2)兄弟S 和 S 的儿子都是黑色的
下面两种情况的区别仅仅是子树根节点的颜色不同, 上面已经解释过了.
在这种情况下,我们简单的重绘 S 为红色。结果是通过S的所有路径,它们就是以前不 通过 N 的那些路径,都少了一个黑色节点。因为删除 N 的初始的父亲使通过 N 的所有路径少了一个黑色节点,这使事情都平衡了起来。但是,通过 P 的所有路径现在比不通过 P 的路径少了一个黑色节点,所以仍然违反属性4。要修正这个问题,我们要从情况 1 开始,在 P 上做重新平衡处理。
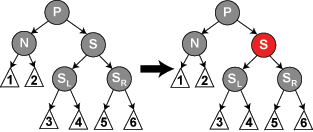
S 和 S 的儿子都是黑色,但是 N 的父亲是红色。在这种情况下,我们简单的交换 N 的兄弟和父亲的颜色。这不影响不通过 N 的路径的黑色节点的数目,但是它在通过 N 的路径上对黑色节点数目增加了一,添补了在这些路径上删除的黑色节点。
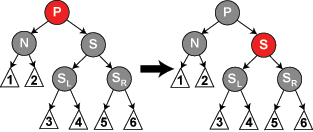
3)S 是黑色,S 的左儿子是红色,S 的右儿子是黑色,而 N 是它父亲的左儿子。在这种情况下我们在 S 上做右旋转,这样 S 的左儿子成为 S 的父亲和 N 的新兄弟。我们接着交换 S 和它的新父亲的颜色。
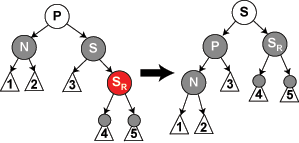
4)S 是黑色,S 的右儿子是红色,而 N 是它父亲的左儿子。在这种情况下我们在 N 的父亲上做左旋转,这样 S 成为 N 的父亲和 S 的右儿子的父亲。我们接着交换 N 的父亲和 S 的颜色,并使 S 的右儿子为黑色。
下面给出红黑树的python实现, 删除没写, 以后有空补
1 class RBTreeNode(Node):
2 """ red-black tree node"""
3 def __init__(self, data):
4 Node.__init__(self, data)
5 self.color = 'red'
6
7 def createNode(self, data):
8 return RBTreeNode(data)
9
10 def pivotLeft(self):
11 """ """
12 p = self.parent
13 l = self.left
14 r = self.right
15 #if has right child, save the left child of it
16 if r:
17 rl= r.left
18 else:
19 return
20 #after left pivot, r become new root of the child tree, so update r.parent
21 if p:
22 if p.left == self:
23 p.left = r
24 else:
25 p.right = r
26 r.parent = p
27 else:
28 r.parent = None
29 # update r.left, r.right not change
30 r.left = self
31 #update self.parent and self.right, left not change
32 self.parent = r
33 self.right = rl
34
35 return self, r
36 def pivotRight(self):
37 """ same logic with pivotLeft, just exchange the r and l"""
38 p = self.parent
39 l = self.left
40 r = self.right
41 if l:
42 lr= l.right
43 else:
44 return
45 if p:
46 if p.left == self:
47 p.left = l
48 else:
49 p.right = l
50 l.parent = p
51 else:
52 l.parent = None
53 l.right = self
54 self.parent = l
55 self.left = lr
56 return self, l
57
58 def insert(self, data):
59 """"""
60 n = Node.insert(self, data)
61 print n.data
62 #rebalance for insert
63 n.rebalance()
64
65 def rebalance(self):
66 """"""
67 n = self
68 p = n.parent
69 if not p:
70 n.black()
71 return
72 g = p.parent
73 #parent is black, no problem
74 if p and p.isBlack(): return
75
76 u = g.getOtherChild(p)
77 #p is red, u is red, then g must be black
78 if p.isRed()and u and u.isRed():
79 p.black()
80 u.black()
81 g.red()
82 g.rebalance()
83
84 #p is red, but u isn't red, black or leaf
85 if p.isRed():
86 if n.isRight() and p.isLeft():
87 print 'nr, pl'
88 p.pivotLeft()
89 n, p = p, n
90 if n.isLeft() and p.isLeft():
91 print 'nl, pl'
92 p.black()
93 g.red()
94 g.pivotRight()
95 return
96
97 if n.isLeft() and p.isRight():
98 print 'nl, pr'
99 p.pivotRight()
100 n, p = p, n
101 if n.isRight() and p.isRight():
102 print 'nr, pr'
103 p.black()
104 g.red()
105 g.pivotLeft()
106 return
107
108
109 def isLeft(self):
110 n = self
111 p = self.parent
112 if p and n == p.left:
113 return True
114 else:
115 return False
116 def isRight(self):
117 n = self
118 p = self.parent
119 if p and n == p.right:
120 return True
121 else:
122 return False
123 def isBlack(self):
124 if self.color == 'black':
125 return True
126 else:
127 return False
128 def isRed(self):
129 if self.color == 'red':
130 return True
131 else:
132 return False
133 def black(self):
134 self.color = 'black'
135 def red(self):
136 self.color = 'red'
137
138 def getOtherChild(self,child):
139 """ Give one child, and return other child"""
140 if self.left == child:
141 return self.right
142 else:
143 return self.left
144
145 def Print(self, indent):
146 for i in range(indent):
147 print " ",
148 print "%s (%s)" % (self.data, self.color)
149 if not self.left:
150 for i in range(indent+1):
151 print " ",
152 print "None(Black)"
153 else:
154 self.left.Print(indent+1)
155 if not self.right:
156 for i in range(indent+1):
157 print " ",
158 print "None(Black)"
159 else:
160 self.right.Print(indent+1)
161
162 class RBTree:
163 """ red-black tree"""
164 def __init__(self):
165 self.root = None
166
167 def insert(self, data):
168 if self.root:
169 self.root.insert(data)
170 self.updateRoot()
171 else:
172 self.root = RBTreeNode(data)
173 self.root.color = 'black'
174
175 def updateRoot(self):
176 """Update root node when root changes"""
177 n = self.root.parent
178 while n:
179 if n.parent:
180 n = n.parent
181 else:
182 break
183 if n:
184 self.root = n
185
186 def Print(self):
187 if self.root == None:
188 print "Empty"
189 else:
190 self.root.Print(1)
191 def buildRBTree():
192 tree = RBTree()
193 for i in range(10):
194 tree.insert(i)
195 tree.Print() |
图
图的表示和搜索
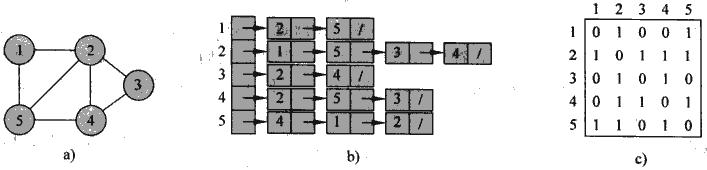
图,G=(V,E) ,的表示两种方法, 邻接表和邻接矩阵. 两者各有利弊, 都可以适用于有向图, 无向图, 加权图
邻接表 , 最常用的表示方法, 适用于稀疏图或比较小的图, 空间复杂度为(V+E), 优点是简单,空间耗费小, 缺点就是确定边是否存在效率低
邻接矩阵 , 用于稠密图或需要迅速判断两点间边存在的场景, 空间复杂度为(V2 ), 优点是判断边存在问题快, 缺点就是空间耗费比较大, 是一种用空间换时间的方法. 有些对空间的优化, 比如对于无向图, 矩阵是对称的, 所以只需要存储一半. 对于非加权图, 每个边只需要用1bit存储.
那么用python怎么表示图, 没有语言直接有图这样的数据结构, 不过对于python而言, 通过字典加上list可以很容易的表示图(http://www.python.org/doc/essays/graphs.html), 例子如下
1 #A -> B
2 #A -> C
3 #B -> C
4 #B -> D
5 #C -> D
6 #D -> C
7 #E -> F
8 #F -> C
9 graph = {'A': ['B', 'C'],
10 'B': ['C', 'D'],
11 'C': ['D'],
12 'D': ['C'],
13 'E': ['F'],
14 'F': ['C']} |
图的搜索方法 分广度优先 和深度优先 两种, 这是最基本的图算法, 也是图算法的核心. 其他的图算法一般都是基于图搜索算法或是它的扩充.
广度优先搜索 (breadth-first search)
广度优先是最简单的图搜索算法之一, 也是许多重要的图算法的原型. 在Prim最小生成树算法和Dijkstra单源最短路径算法中, 都采用了类似的思想.
顾名思义, 给定一个源顶点s, 广度优先算法会沿其广度方向向外扩展, 即先发现和s距离为k的所有顶点, 然后才发现和s距离为k+1的所有顶点.
显然这样的搜索方式, 按照节点被发现的顺序, 最终会生成一棵树, 称之为广度优先树 , 每个节点至多被发现一次(第一次, 后面再遍历到就不算了), 仅当节点被发现时, 他的前趋节点为他的父节点, 所以广度优先树又形式化的称为该图的前趋子图 .
我们还可以证明, 在广度优先树, 任意节点到源顶点s的距离(树高)为他们之间的最短距离 .
这个很容易证明, 假设在广度优先树上该节点n到s的距离为k, 而n到s的最短距离为k-1.
由于是广度优先搜索, 必须要先发现和s距离为k-1的所有顶点, 然后才会去发现和s距离为k的顶点, 所以产生矛盾, 在广度优先树上距离应该是k-1, 而不可能是k, 从而得证这就是最短距离.
所以广度优先算法可用于求图中两点间(a,b)的无权最短路径. 方法首先以a为源求前趋子图(即广度优先树), 然后在树中找到b, 不断求其前趋, 到a为止, 中间经过的节点就是其最短路径. 如果无法达到a, 则a,b间不可达.
实现如下, 在实现BFS算法时, 我们需要用到queue数据结构, 来存放仍需继续搜索的节点...
1 def BFS(graph, start):
2 parent = {start:None}
3 dist = {start:0}
4 queue = [start]
5
6 while queue:
7 v = queue.pop(0)
8 print v
9 e = graph[v]
10 for n in e:
11 if not parent.get(n) and not dist.get(n):
12 parent[n] = v
13 dist[n]= dist[v]+1
14 queue.append(n)
15 print n, parent[n], dist[n]
16 return parent
17
18 def shortestPath(parent, start, end):
19 if start == end:
20 print start
21 return
22 p = parent.get(end)
23 if not p:
24 print 'no path'
25 return
26 shortestPath(parent, start, p)
27 print end
28 if __name__ == "__main__":
29 graph = {'A': ['B', 'C','E'],
30 'B': ['A','C', 'D'],
31 'C': ['D'],
32 'D': ['C'],
33 'E': ['F','D'],
34 'F': ['C']}
35 p = BFS(graph,'A')
36 shortestPath(p, 'A', 'F') |
深度优先搜索 (Depth-first search)
深度优先搜索所遵循的搜索策略是尽可能“深”地搜索图。在深度优先搜索中,对于最新发现的顶点,如果它还有以此为起点而未探测到的边,就沿此边继续汉下去。当结点v的所有边都己被探寻过,搜索将回溯 到发现结点v有那条边的始结点。这一过程一直进行到已发现从源结点可达的所有结点为止。
深度优先搜索所要回答的基本问题是"What parts of the graph are reachable from a given vertex ", 这其实就是历史悠久的迷宫问题, 在入口点是否可以达到出口点, 这就是深度优先最基本的应用. 科学来源于生活, "Everybody knows that all you need to explore a labyrinth is a ball of string and a piece of chalk.", 对于迷宫我们必须有粉笔和线团 , 粉笔是用来标记走过的路, 防止陷入cycle, 线团是用来准确的回溯到上一个路口.
那么怎么用程序来模拟粉笔和线团来实现深度优先搜索, 粉笔很容易解决, 对每个节点用0/1来表示是否已访问. 而线团就需要用stack来表示, push就是unwind, pop就是rewind, 是不是很有意思. 基于这个思路任何迷宫都是可解的. 而往往stack也是用隐形的方式来实现的, 通过函数递归. 我下面的实现即给出了递归函数的实现, 也给出了直接用stack的实现, 更清晰的看出chalk的使用方式.
1 pre = {}
2 post = {}
3 clock = 1
4 stack = []
5 def DFS(graph):
6 global pre
7 for v in graph.keys():
8 if not pre.get(v):
9 visit_stack(graph, v)
10
11 def visit(graph, v):
12 global pre
13 global post
14 global clock
15 pre[v] = clock
16 clock = clock + 1
17 print v, pre[v]
18 edges = graph[v]
19 for e in edges:
20 if not pre.get(e):
21 visit(graph, e)
22 post[v] = clock
23 clock = clock + 1
24 print v, pre[v], post[v]
25
26 def visit_stack(graph, v):
27 """
28 use stack to replace recursion
29 """
30 global pre
31 global post
32 global clock
33 global stack
34 stack.append(v)
35 while stack:
36 print stack
37 next = stack.pop()
38 print 'pop:', next
39 while next:
40 if not pre.get(next):
41 pre[next] = clock
42 clock = clock + 1
43 print next, pre[next]
44 edges = graph.get(next)
45 vec = get_white_v(edges)
46 if vec:
47 print 'push:', next
48 stack.append(next)
49 else:
50 post[next] = clock
51 clock = clock + 1
52 print next, pre[next], post[next]
53 next = vec
54
55 def get_white_v(edges):
56 global pre
57 for e in edges:
58 if not pre.get(e):
59 return e
60 return None |
依据深度优先搜索可以获得有关图的结构的大量信息。深度优先搜索所要解决的基本问题是可达性问题, 即连通性问题, 通过这个算法, 我们可以轻松的找到所有连通子图 , 对于每个子图可以生成一个深度优先树, 从而深度优先搜索最终产生的是深度优先森林 .
除此之外, 深度优先搜索还能得到的很重要的信息是, for each node, we will note down the times of two important events, the moment of first discovery (corresponding to previsit ) and that of final departure (postvisit ). 即在第一次发现该节点, 和完成该节点所有相邻节点遍历时, 记下两个时间戳(如下图).
然后基于previsit和postvisit, 就有一些有趣的推论,
1. 子树的源点一定是previsit最小, 而postvisit最大, 因为是递归, 最先开始的最后完成.
2. 对于两个节点u,v, 如果存在后裔和祖先的关系, 那么祖先区间(pre(u),post(u))必定包含后裔区间(pre(v),post(v)). 如果u,v两个区间没有包含关系(完全分离的), 那就一定不存在后裔祖先关系.
3. 图中的边由此也可以分为几类,
树枝 (tree),是深度优先森林中的边,如果结点v是在探寻边(u,v)时第一次被发现,那么边(u,v)就是一个树枝。
反向边 (back),是深度优先树中连结结点u到它的祖先v的那些边,环也被认为是反向边。
正向边 (forward),是指深度优先树中连接顶点u到它的后裔的非树枝的边。
交叉边 (cross),是指所有其他类型的边, 即两个节点的区间完全分离.
这样就可以引出深度优先搜索的第二个应用, 有向无环图(Directed acyclic graphs, Dags)的拓扑排序问题
Dags are good for modeling relations like causalities(因果关系), hierarchies(层级关系), and temporal dependencies(时间依赖关系).
这个在日常生活中经常会碰到这样的情况, 一堆事情之间有因果, 时间关系, 先做谁, 后做谁, 这个就是典型的拓扑排序问题.
下面的图可以给出一个穿衣服的例子,
拓扑排序的实现很简单, 有两种思路,
1. 对图完成深度优先搜索, 然后按节点的postvisit递减排列就得到了拓扑排序.
2. 第二种思路不依赖于postvisit, 首先选择一个无前驱的顶点(即入度为0的顶点,图中至少应有一个这样的顶点,否则肯定存在回路),然后从图中移去该顶点以及由他发出的所有有向边,如果图中还存在无前驱的顶点,则重复上述操作,直到操作无法进行。如果图不为空,说明图中存在回路,无法进行拓扑排序;否则移出的顶点的顺序就是对该图的一个拓扑排序。
前面讨论的无向图的连通性, 对于有向图的连通性问题, 更加复杂一点, 对于有向图必须互相可达, 才认为是连通的.
在有向图G中,如果任意两个不同的顶点相互可达 ,则称该有向图是强连通 的。有向图G的极大强连通子图称为G的强连通分支 。
把有向图分解为强连通分支是深度优先搜索的一个经典应用实例. 很多有关有向图的算法都从分解步骤开始,这种分解可把原始的问题分成数个子问题,其中每个子子问题对应一个强连通分支。构造强连通分支之间的联系也就把子问题的解决方法联系在一起,我们可以用一种称之为分支图的图来表示这种构造, 而分支图一定是dags.
通过深度优先搜索来把有向图分解为强连通分支的方法也很简单,
procedure Strongly_Connected_Components(G);
begin
1.调用DFS(G)以计算出每个结点u的完成时刻post[u];
2.计算出GT ;
3.调用DFS(GT ),但在DFS的主循环里按针post[u]递减的顺序考虑各结点(和第一行中一样计算);
4.输出第3步中产生的深度优先森林中每棵树的结点,作为各自独立的强连通支。
end;
为什么这样就可以找到强连通分支, 从上面的图可知, 图与转置图的强连通分支是一样的. 先对G完成DFS, 然后按post递减的顺序,
现在基于分支图来考虑, 分支图是dag, 所以其实求强连通分支和拓扑排序的思路有些相似, 先DFS(G), 并按post递减的排序, 其实就是把分支(component)进行了拓扑排序, 如果我们能够找到第一个强连通分支, 把它删除, 再继续往下一个个可以找出所有的强连通分支.
为什么要按拓扑排序的顺序找, 因为分支图里面post最大的那个分支, 只有出度无入度, 当取图的转置图时, 就变成了没有出度, 所以对转置图进行深度优先搜索不会找到其他分支的节点, 可以准确的找出属于第一个强连通分支的所有节点. 所以上面算法中, 对转置图按post递减进行深度优先搜索就可以按分支图的拓扑顺序找出所有强连通分支.
1 def transpose(graph):
2 """
3 create transposed graph
4 """
5 t_graph = {}
6
7 for key, edges in graph.items():
8 for edge in edges:
9 if not t_graph.get(edge):
10 t_graph[edge] = [key]
11 else:
12 t_graph[edge].append(key)
13 #print t_graph
14 return t_graph
15 def SCC(graph):
16 """
17 Strongly_Connected_Components
18 """
19 global post
20 global pre
21 global clock
22 DFS(graph)
23 p = post.items()
24 p.sort(key=lambda x:x[1],reverse=True)
25 print p
26 t_graph = transpose(graph)
27 post = {}
28 pre = {}
29 clock = 1
30 for v,num in p:
31 if not pre.get(v):
32 print v, '=========================='
33 visit(t_graph, v) |
广度和深度优先搜索的区别
对于这两种算法基本的目的都是要遍历所有节点一次, 所以时间复杂度是一致的O(V+E)
两者在实现上唯一的区别是, BFS使用Queue, 而DFS使用Stack, 这就是两者所有区别的根源, Queue的先进先出特性确保了只有上一层的所有节点都被访问过, 才会开始访问下层节点, 从而保证了广度优先, 而Stack的先进后出的特性, 会从叶节点不断回溯, 从而达到深度优先.
两者应用场景不同, BFS比较简单, 主要用于求最短路径, DFS复杂些, 主要用于graph decomposition, 即怎样把一个图分解成相互连通的子图, 其中包含了有向图的拓扑排序问题. |