引言和数据
欢迎阅读 Python 机器学习系列教程的回归部分。这里,你应该已经安装了 Scikit-Learn。如果没有,安装它,以及
Pandas 和 Matplotlib。
| pip install numpy
pip install scipy
pip install scikit-learn
pip install matplotlib
pip install pandas |
除了这些教程范围的导入之外,我们还要在这里使用 Quandl:
首先,对于我们将其用于机器学习而言,什么是回归呢?它的目标是接受连续数据,寻找最适合数据的方程,并能够对特定值进行预测。使用简单的线性回归,你可以仅仅通过创建最佳拟合直线,来实现它。
这里,我们可以使用这条直线的方程,来预测未来的价格,其中日期是 x 轴。
回归的热门用法是预测股票价格。由于我们会考虑价格随时间的流动,并且使用连续的数据集,尝试预测未来的下一个流动价格,所以可以这样做。
回归是监督的机器学习的一种,也就是说,科学家向其展示特征,之后向其展示正确答案来教会机器。一旦教会了机器,科学家就能够使用一些不可见的数据来测试机器,其中科学家知道正确答案,但是机器不知道。机器的答案会与已知答案对比,并且度量机器的准确率。如果准确率足够高,科学家就会考虑将其算法用于真实世界。
由于回归广泛用于股票价格,我们可以使用一个示例从这里开始。最开始,我们需要数据。有时候数据易于获取,有时你需要出去并亲自收集。我们这里,我们至少能够以简单的股票价格和成交量信息开始,它们来自
Quandl。我们会抓取 Google 的股票价格,它的代码是GOOGL:
| import
pandas as pd
import quandl
df = quandl.get("WIKI/GOOGL")
print(df.head())
|
注意:写这篇文章的时候,Quandl 的模块使用大写 Q 引用,但现在是小写 q,所以import
quandl。
到这里,我们拥有:
| Open
High Low Close Volume Ex-Dividend \
Date
2004-08-19 100.00 104.06 95.96 100.34 44659000
0
2004-08-20 101.01 109.08 100.50 108.31 22834300
0
2004-08-23 110.75 113.48 109.05 109.40 18256100
0
2004-08-24 111.24 111.60 103.57 104.87 15247300
0
2004-08-25 104.96 108.00 103.88 106.00 9188600
0
Split Ratio Adj. Open Adj. High Adj. Low Adj.
Close \
Date
2004-08-19 1 50.000 52.03 47.980 50.170
2004-08-20 1 50.505 54.54 50.250 54.155
2004-08-23 1 55.375 56.74 54.525 54.700
2004-08-24 1 55.620 55.80 51.785 52.435
2004-08-25 1 52.480 54.00 51.940 53.000
Adj. Volume
Date
2004-08-19 44659000
2004-08-20 22834300
2004-08-23 18256100
2004-08-24 15247300
2004-08-25 9188600
|
这是个非常好的开始,我们拥有了数据,但是有点多了。
这里,我们有很多列,许多都是多余的,还有些不怎么变化。我们可以看到,常规和修正(Adj)的列是重复的。修正的列看起来更加理想。常规的列是当天的价格,但是股票有个叫做分拆的东西,其中一股突然就变成了两股,所以一股的价格要减半,但是公司的价值不变。修正的列为股票分拆而调整,这使得它们对于分析更加可靠。
所以,让我们继续,削减原始的 DataFrame。
| df
= df[['Adj. Open', 'Adj. High', 'Adj. Low',
'Adj. Close', 'Adj. Volume']]
|
现在我们拥有了修正的列,以及成交量。有一些东西需要注意。许多人谈论或者听说机器学习,就像无中生有的黑魔法。机器学习可以突出已有的数据,但是数据需要先存在。你需要有意义的数据。所以你怎么知道是否有意义呢?我的最佳建议就是,仅仅简化你的大脑。考虑一下,历史价格会决定未来价格吗?有些人这么认为,但是久而久之这被证实是错误的。但是历史规律呢?突出的时候会有意义(机器学习会有所帮助),但是还是太弱了。那么,价格变化和成交量随时间的关系,再加上历史规律呢?可能更好一点。所以,你已经能够看到,并不是数据越多越好,而是我们需要使用有用处的数据。同时,原始数据应该做一些转换。
考虑每日波动,例如最高价减最低价的百分比差值如何?每日的百分比变化又如何呢?你觉得Open, High,
Low, Close这种简单数据,还是Close, Spread/Volatility, %change
daily更好?我觉得后者更好一点。前者都是非常相似的数据点,后者基于前者的统一数据创建,但是带有更加有价值的信息。
所以,并不是你拥有的所有数据都是有用的,并且有时你需要对你的数据执行进一步的操作,并使其更加有价值,之后才能提供给机器学习算法。让我们继续并转换我们的数据:
| df['HL_PCT']
= (df['Adj. High'] - df['Adj. Low']) / df['Adj.
Close'] * 100.0 |
这会创建一个新的列,它是基于收盘价的百分比极差,这是我们对于波动的粗糙度量。下面,我们会计算每日百分比变化:
| df['PCT_change']
= (df['Adj. Close'] - df['Adj. Open']) / df['Adj.
Open'] * 100.0 |
现在我们会定义一个新的 DataFrame:
| df
= df[['Adj. Close', 'HL_PCT', 'PCT_change',
'Adj. Volume']]
print(df.head()) |
|
Adj. Close HL_PCT PCT_change Adj. Volume
Date
2004-08-19 50.170 8.072553 0.340000 44659000
2004-08-20 54.155 7.921706 7.227007 22834300
2004-08-23 54.700 4.049360 -1.218962 18256100
2004-08-24 52.435 7.657099 -5.726357 15247300
2004-08-25 53.000 3.886792 0.990854 9188600 |
特征和标签
基于上一篇机器学习回归教程,我们将要对我们的股票价格数据执行回归。目前的代码:
| import
quandl
import pandas as pd
df = quandl.get("WIKI/GOOGL")
df = df[['Adj. Open', 'Adj. High', 'Adj. Low',
'Adj. Close', 'Adj. Volume']]
df['HL_PCT'] = (df['Adj. High'] - df['Adj. Low'])
/ df['Adj. Close'] * 100.0
df['PCT_change'] = (df['Adj. Close'] - df['Adj.
Open']) / df['Adj. Open'] * 100.0
df = df[['Adj. Close', 'HL_PCT', 'PCT_change',
'Adj. Volume']]
print(df.head()) |
这里我们已经获取了数据,判断出有价值的数据,并通过操作创建了一些。我们现在已经准备好使用回归开始机器学习的过程。首先,我们需要一些更多的导入。所有的导入是:
| import
quandl, math
import numpy as np
import pandas as pd
from sklearn import preprocessing, cross_validation,
svm
from sklearn.linear_model import LinearRegression |
我们会使用numpy模块来将数据转换为 NumPy 数组,它是 Sklearn 的预期。我们在用到preprocessing和cross_validation时,会深入谈论他们,但是预处理是用于在机器学习之前,对数据清洗和缩放的模块。交叉验证在测试阶段使用。最后,我们也从
Sklearn 导入了LinearRegression算法,以及svm。它们用作我们的机器学习算法来展示结果。
这里,我们已经获取了我们认为有用的数据。真实的机器学习如何工作呢?使用监督式学习,你需要特征和标签。特征就是描述性属性,标签就是你尝试预测的结果。另一个常见的回归示例就是尝试为某个人预测保险的保费。保险公司会收集你的年龄、驾驶违规行为、公共犯罪记录,以及你的信用评分。公司会使用老客户,获取数据,并得出应该给客户的“理想保费”,或者如果他们觉得有利可图的话,他们会使用实际使用的客户。
所以,对于训练机器学习分类器来说,特征是客户属性,标签是和这些属性相关的保费。
我们这里,什么是特征和标签呢?我们尝试预测价格,所以价格就是标签?如果这样,什么是特征呢?对于预测我们的价格来说,我们的标签,就是我们打算预测的东西,实际上是未来价格。这样,我们的特征实际上是:当前价格、HL
百分比和百分比变化。标签价格是未来某个点的价格。让我们继续添加新的行:
| forecast_col
= 'Adj. Close'
df.fillna(value=-99999, inplace=True)
forecast_out = int(math.ceil(0.01 * len(df))) |
这里,我们定义了预测列,之后我们将任何 NaN 数据填充为 -99999。对于如何处理缺失数据,你有一些选择,你不能仅仅将
NaN(不是数值)数据点传给机器学习分类西,你需要处理它。一个主流选项就是将缺失值填充为 -99999。在许多机器学习分类器中,会将其是被为离群点。你也可以仅仅丢弃包含缺失值的所有特征或标签,但是这样你可能会丢掉大量的数据。
真实世界中,许多数据集都很混乱。多数股价或成交量数据都很干净,很少有缺失数据,但是许多数据集会有大量缺失数据。我见过一些数据集,大量的行含有缺失数据。你并不一定想要失去所有不错的数据,如果你的样例数据有一些缺失,你可能会猜测真实世界的用例也有一些缺失。你需要训练、测试并依赖相同数据,以及数据的特征。
最后,我们定义我们需要预测的东西。许多情况下,就像尝试预测客户的保费的案例中,你仅仅需要一个数字,但是对于预测来说,你需要预测指定数量的数据点。我们假设我们打算预测数据集整个长度的
1%。因此,如果我们的数据是 100 天的股票价格,我们需要能够预测未来一天的价格。选择你想要的那个。如果你只是尝试预测明天的价格,你应该选取一天之后的数据,而且也只能一天之后的数据。如果你打算预测
10 天,我们可以为每一天生成一个预测。
我们这里,我们决定了,特征是一系列当前值,标签是未来的价格,其中未来是数据集整个长度的 1%。我们假设所有当前列都是我们的特征,所以我们使用一个简单的
Pnadas 操作添加一个新的列:
| df['label']
= df[forecast_col].shift(-forecast_out) |
现在我们拥有了数据,包含特征和标签。下面我们在实际运行任何东西之前,我们需要做一些预处理和最终步骤,我们在下一篇教程会关注。
训练和测试
欢迎阅读 Python 机器学习系列教程的第四部分。在上一个教程中,我们获取了初始数据,按照我们的喜好操作和转换数据,之后我们定义了我们的特征。Scikit
不需要处理 Pandas 和 DataFrame,我出于自己的喜好而处理它,因为它快并且高效。反之,Sklearn
实际上需要 NumPy 数组。Pandas 的 DataFrame 可以轻易转换为 NumPy 数组,所以事情就是这样的。
目前为止我们的代码:
| import
quandl, math
import numpy as np
import pandas as pd
from sklearn import preprocessing, cross_validation,
svm
from sklearn.linear_model import LinearRegression
df = quandl.get("WIKI/GOOGL")
print(df.head())
#print(df.tail())
df = df[['Adj. Open', 'Adj. High', 'Adj. Low',
'Adj. Close', 'Adj. Volume']]
df['HL_PCT'] = (df['Adj. High'] - df['Adj.
Low']) / df['Adj. Close'] * 100.0
df['PCT_change'] = (df['Adj. Close'] - df['Adj.
Open']) / df['Adj. Open'] * 100.0
df = df[['Adj. Close', 'HL_PCT', 'PCT_change',
'Adj. Volume']]
print(df.head())
forecast_col = 'Adj. Close'
df.fillna(value=-99999, inplace=True)
forecast_out = int(math.ceil(0.01 * len(df)))
df['label'] = df[forecast_col].shift(-forecast_out) |
我们之后要丢弃所有仍旧是 NaN 的信息。
对于机器学习来说,通常要定义X(大写)作为特征,和y(小写)作为对于特征的标签。这样,我们可以定义我们的特征和标签,像这样:
| X
= np.array(df.drop(['label'], 1))
y = np.array(df['label']) |
上面,我们所做的就是定义X(特征),是我们整个的 DataFrame,除了label列,并转换为 NumPy
数组。我们使用drop方法,可以用于 DataFrame,它返回一个新的 DataFrame。下面,我们定义我们的y变量,它是我们的标签,仅仅是
DataFrame 的标签列,并转换为 NumPy 数组。
现在我们就能告一段落,转向训练和测试了,但是我们打算做一些预处理。通常,你希望你的特征在 -1 到
1 的范围内。这可能不起作用,但是通常会加速处理过程,并有助于准确性。因为大家都使用这个范围,它包含在了
Sklearn 的preprocessing模块中。为了使用它,你需要对你的X变量调用preprocessing.scale。
| X
= preprocessing.scale(X) |
下面,创建标签y:
| y
= np.array(df['label']) |
现在就是训练和测试的时候了。方式就是选取 75% 的数据用于训练机器学习分类器。之后选取剩下的 25%
的数据用于测试分类器。由于这是你的样例数据,你应该拥有特征和一直标签。因此,如果你测试后 25% 的数据,你就会得到一种准确度和可靠性,叫做置信度。有许多方式可以实现它,但是,最好的方式可能就是使用内建的cross_validation,因为它也会为你打乱数据。代码是这样:
| X_train,
X_test, y_train, y_test = cross_validation.train_test_split(X,
y, test_size=0.2) |
这里的返回值是特征的训练集、测试集、标签的训练集和测试集。现在,我们已经定义好了分类器。Sklearn
提供了许多通用的分类器,有一些可以用于回归。我们会在这个例子中展示一些,但是现在,让我们使用svm包中的支持向量回归。
我们这里仅仅使用默认选项来使事情简单,但是你可以在sklearn.svm.SVR的文档中了解更多。
一旦你定义了分类器,你就可以训练它了。在 Sklearn 中,使用fit来训练。
| clf.fit(X_train,
y_train)1 |
这里,我们拟合了我们的训练特征和训练标签。
我们的分类器现在训练完毕。这非常简单,现在我们可以测试了。
| confidence
= clf.score(X_test, y_test) |
加载测试,之后:
| print(confidence)
# 0.960075071072 |
所以这里,我们可以看到准确率几乎是 96%。没有什么可说的,让我们尝试另一个分类器,这一次使用LinearRegression:
| clf
= LinearRegression()
# 0.963311624499 |
更好一点,但是基本一样。所以作为科学家,我们如何知道,选择哪个算法呢?不久,你会熟悉什么在多数情况下都工作,什么不工作。你可以从
Scikit 的站点上查看选择正确的评估工具。这有助于你浏览一些基本的选项。如果你询问搞机器学习的人,它完全是试验和出错。你会尝试大量的算法并且仅仅选取最好的那个。要注意的另一件事情就是,一些算法必须线性运行,其它的不是。不要把线性回归和线性运行搞混了。所以这些意味着什么呢?一些机器学习算法会一次处理一步,没有多线程,其它的使用多线程,并且可以利用你机器上的多核。你可以深入了解每个算法,来弄清楚哪个可以多线程,或者你可以阅读文档,并查看n_jobs参数。如果拥有n_jobs,你就可以让算法通过多线程来获取更高的性能。如果没有,就很不走运了。所以,如果你处理大量的数据,或者需要处理中等规模的数据,但是需要很高的速度,你就可能想要线程加速。让我们看看这两个算法。
访问sklearn.svm.SVR的文档,并查看参数,看到n_jobs了嘛?反正我没看到,所以它就不能使用线程。你可能会看到,在我们的小型数据集上,差异不大。但是,假设数据集由
20MB,差异就很明显。然后,我们查看LinearRegression算法,看到n_jobs了嘛?当然,所以这里,你可以指定你希望多少线程。如果你传入-1,算法会使用所有可用的线程。
这样:
| clf
= LinearRegression(n_jobs=-1) |
就够了。虽然我让你做了很少的事情(查看文档),让我给你说个事实吧,仅仅由于机器学习算法使用默认参数工作,不代表你可以忽略它们。例如,让我们回顾svm.SVR。SVR
是支持向量回归,在执行机器学习时,它是一种架构。我非常鼓励那些有兴趣学习更多的人,去研究这个主题,以及向比我学历更高的人学习基础。我会尽力把东西解释得更简单,但是我并不是专家。回到刚才的话题,svm.SVR有一个参数叫做kernel。这个是什么呢?核就相当于你的数据的转换。这使得处理过程更加迅速。在svm.SVR的例子中,默认值是rbf,这是核的一个类型,你有一些选择。查看文档,你可以选择'linear',
'poly', 'rbf', 'sigmoid', 'precomputed'或者一个可调用对象。同样,就像尝试不同的
ML 算法一样,你可以做你想做的任何事情,尝试一下不同的核吧。
| for
k in ['linear','poly','rbf','sigmoid']:
clf = svm.SVR(kernel=k)
clf.fit(X_train, y_train)
confidence = clf.score(X_test, y_test)
print(k,confidence)1
linear 0.960075071072
poly 0.63712232551
rbf 0.802831714511
sigmoid -0.125347960903
|
我们可以看到,线性的核表现最好,之后是rbf,之后是poly,sigmoid很显然是个摆设,并且应该移除。
所以我们训练并测试了数据集。我们已经有 71% 的满意度了。下面我们做什么呢?现在我们需要再进一步,做一些预测,下一章会涉及它。
预测
欢迎阅读机器学习系列教程的第五章,当前涉及到回归。目前为止,我们收集并修改了数据,训练并测试了分类器。这一章中,我们打算使用我们的分类器来实际做一些预测。我们目前所使用的代码为:
| import
quandl, math
import numpy as np
import pandas as pd
from sklearn import preprocessing, cross_validation,
svm
from sklearn.linear_model import LinearRegression
df = quandl.get("WIKI/GOOGL")
df = df[['Adj. Open', 'Adj. High', 'Adj. Low',
'Adj. Close', 'Adj. Volume']]
df['HL_PCT'] = (df['Adj. High'] - df['Adj. Low'])
/ df['Adj. Close'] * 100.0
df['PCT_change'] = (df['Adj. Close'] - df['Adj.
Open']) / df['Adj. Open'] * 100.0
df = df[['Adj. Close', 'HL_PCT', 'PCT_change',
'Adj. Volume']]
forecast_col = 'Adj. Close'
df.fillna(value=-99999, inplace=True)
forecast_out = int(math.ceil(0.01 * len(df)))
df['label'] = df[forecast_col].shift(-forecast_out)
X = np.array(df.drop(['label'], 1))
X = preprocessing.scale(X)
X = X[:-forecast_out]
df.dropna(inplace=True)
y = np.array(df['label'])
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X,
y, test_size=0.2)
clf = LinearRegression(n_jobs=-1)
clf.fit(X_train, y_train)
confidence = clf.score(X_test, y_test)
print(confidence) |
我会强调,准确率大于 95% 的线性模型并不是那么好。我当然不会用它来交易股票。仍然有一些需要考虑的问题,特别是不同公司有不同的价格轨迹。Google
非常线性,向右上角移动,许多公司不是这样,所以要记住。现在,为了做预测,我们需要一些数据。我们决定预测
1% 的数据,因此我们打算,或者至少能够预测数据集的后 1%。所以我们什么可以这样做呢?我们什么时候可以识别这些数据?我们现在就可以,但是要注意我们尝试预测的数据,并没有像训练集那样缩放。好的,那么做什么呢?是否要对后
1% 调用preprocessing.scale()?缩放方法基于所有给它的已知数据集。理想情况下,你应该一同缩放训练集、测试集和用于预测的数据。这永远是可能或合理的嘛?不是,如果你可以这么做,你就应该这么做。但是,我们这里,我们可以这么做。我们的数据足够小,并且处理时间足够低,所以我们会一次性预处理并缩放数据。
在许多例子中,你不能这么做。想象如果你使用几个 GB 的数据来训练分类器。训练分类器会花费几天,不能在每次想要做出预测的时候都这么做。因此,你可能需要不缩放任何东西,或者单独缩放数据。通常,你可能希望测试这两个选项,并看看那个对于你的特定案例更好。
要记住它,让我们在定义X的时候处理所有行:
| X
= np.array(df.drop(['label'], 1))
X = preprocessing.scale(X)
X_lately = X[-forecast_out:]
X = X[:-forecast_out]
df.dropna(inplace=True)
y = np.array(df['label'])
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X,
y, test_size=0.2)
clf = LinearRegression(n_jobs=-1)
clf.fit(X_train, y_train)
confidence = clf.score(X_test, y_test)
print(confidence) |
要注意我们首先获取所有数据,预处理,之后再分割。我们的X_lately变量包含最近的特征,我们需要对其进行预测。目前你可以看到,定义分类器、训练、和测试都非常简单。预测
| forecast_set
= clf.predict(X_lately) |
也非常简单:
forecast_set是预测值的数组,表明你不仅仅可以做出单个预测,还可以一次性预测多个值。看看我们目前拥有什么:
| [
745.67829395 737.55633261 736.32921413 717.03929303
718.59047951
731.26376715 737.84381394 751.28161162 756.31775293
756.76751056
763.20185946 764.52651181 760.91320031 768.0072636
766.67038016
763.83749414 761.36173409 760.08514166 770.61581391
774.13939706
768.78733341 775.04458624 771.10782342 765.13955723
773.93369548
766.05507556 765.4984563 763.59630529 770.0057166
777.60915879] 0.956987938167 30 |
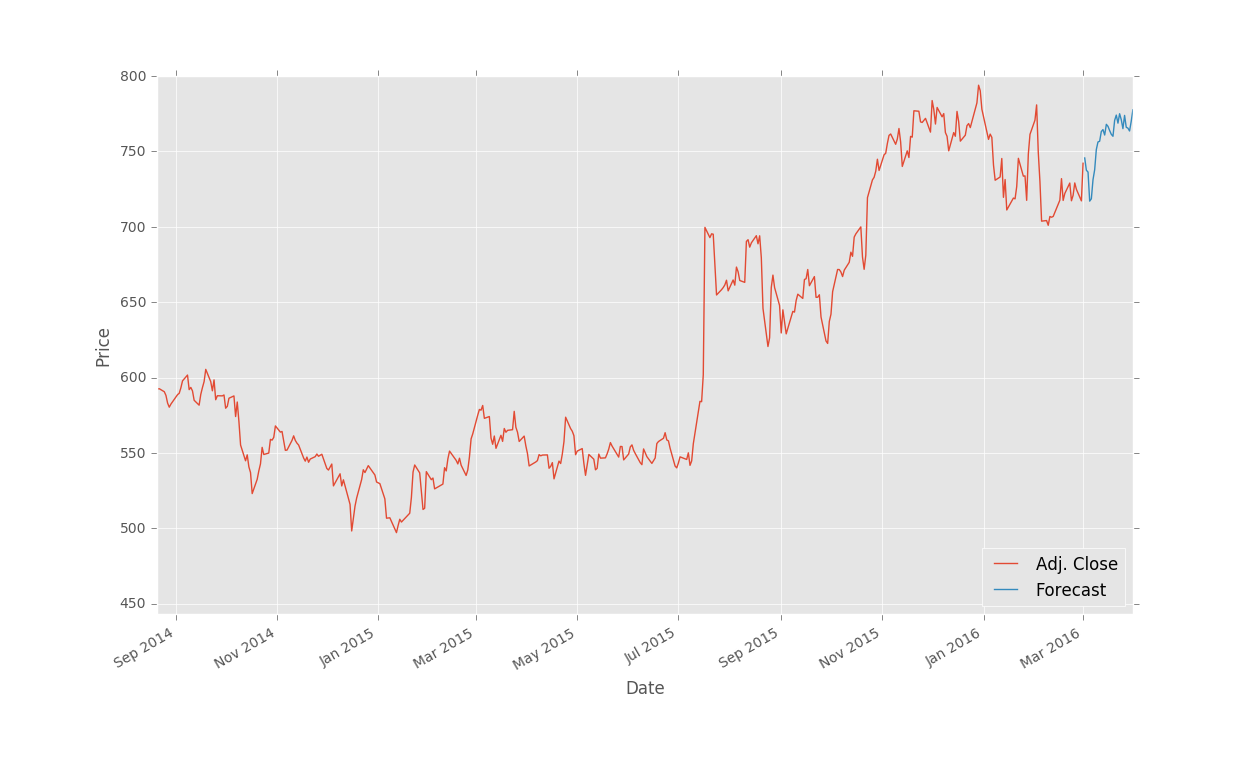
所以这些就是我们的预测结果,然后呢?已经基本完成了,但是我们可以将其可视化。股票价格是每一天的,一周
5 天,周末没有。我知道这个事实,但是我们打算将其简化,把每个预测值当成每一天的。如果你打算处理周末的间隔(不要忘了假期),就去做吧,但是我这里会将其简化。最开始,我们添加一些新的导入:
| import
datetime
import matplotlib.pyplot as plt
from matplotlib import style |
我导入了datetime来处理datetime对象,Matplotlib 的pyplot包用于绘图,以及style来使我们的绘图更加时髦。让我们设置一个样式:
之后,我们添加一个新的列,forecast列:
我们首先将值设置为 NaN,但是我们之后会填充他。
预测集的标签正好从明天开始。因为我们要预测未来m = 0.1 * len(df)天的数据,相当于把收盘价往前移动m天生成标签。那么数据集的后m个是不能用作训练集和测试集的,因为没有标签。于是我们将后m个数据用作预测集。预测集的第一个数据,也就是数据集的第n
- m个数据,它的标签应该是n - m + m = n天的收盘价,我们知道今天在df里面是第n -
1天,那么它就是明天。
我们首先需要抓取 DataFrame 的最后一天,将每一个新的预测值赋给新的日期。我们会这样开始。
| last_date
= df.iloc[-1].name
last_unix = last_date.timestamp()
one_day = 86400
next_unix = last_unix + one_day |
现在我们拥有了预测集的起始日期,并且一天有 86400 秒。现在我们将预测添加到现有的 DataFrame
中。
| for
i in forecast_set:
next_date = datetime.datetime.fromtimestamp(next_unix)
next_unix += 86400
df.loc[next_date] = [np.nan for _ in range(len(df.columns)-1)]+[i] |
我们这里所做的是,迭代预测集的标签,获取每个预测值和日期,之后将这些值放入 DataFrame(使预测集的特征为
NaN)。最后一行的代码创建 DataFrame 中的一行,所有元素置为 NaN,然后将最后一个元素置为i(这里是预测集的标签)。我选择了这种单行的for循环,以便在改动
DataFrame 和特征之后,代码还能正常工作。所有东西都做完了吗?将其绘制出来。
| df['Adj.
Close'].plot()
df['Forecast'].plot()
plt.legend(loc=4)
plt.xlabel('Date')
plt.ylabel('Price')
plt.show() |
完整的代码:
| import
Quandl, math
import numpy as np
import pandas as pd
from sklearn import preprocessing, cross_validation,
svm
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
from matplotlib import style
import datetime
style.use('ggplot')
df = Quandl.get("WIKI/GOOGL")
df = df[['Adj. Open', 'Adj. High', 'Adj. Low',
'Adj. Close', 'Adj. Volume']]
df['HL_PCT'] = (df['Adj. High'] - df['Adj. Low'])
/ df['Adj. Close'] * 100.0
df['PCT_change'] = (df['Adj. Close'] - df['Adj.
Open']) / df['Adj. Open'] * 100.0
df = df[['Adj. Close', 'HL_PCT', 'PCT_change',
'Adj. Volume']]
forecast_col = 'Adj. Close'
df.fillna(value=-99999, inplace=True)
forecast_out = int(math.ceil(0.01 * len(df)))
df['label'] = df[forecast_col].shift(-forecast_out)
X = np.array(df.drop(['label'], 1))
X = preprocessing.scale(X)
X_lately = X[-forecast_out:]
X = X[:-forecast_out]
df.dropna(inplace=True)
y = np.array(df['label'])
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X,
y, test_size=0.2)
clf = LinearRegression(n_jobs=-1)
clf.fit(X_train, y_train)
confidence = clf.score(X_test, y_test)
forecast_set = clf.predict(X_lately)
df['Forecast'] = np.nan
last_date = df.iloc[-1].name
last_unix = last_date.timestamp()
one_day = 86400
next_unix = last_unix + one_day
for i in forecast_set:
next_date = datetime.datetime.fromtimestamp(next_unix)
next_unix += 86400
df.loc[next_date] = [np.nan for _ in range(len(df.columns)-1)]+[i]
df['Adj. Close'].plot()
df['Forecast'].plot()
plt.legend(loc=4)
plt.xlabel('Date')
plt.ylabel('Price')
plt.show() |
结果:
保存和扩展
上一篇教程中,我们使用回归完成了对股票价格的预测,并使用 Matplotlib 可视化。这个教程中,我们会讨论一些接下来的步骤。
我记得我第一次尝试学习机器学习的时候,多数示例仅仅涉及到训练和测试的部分,完全跳过了预测部分。对于那些包含训练、测试和预测部分的教程来说,我没有找到一篇解释保存算法的文章。在那些例子中,数据通常非常小,所以训练、测试和预测过程都很快。在真实世界中,数据都非常大,并且花费更长时间来处理。由于没有一篇教程真正谈论到这一重要的过程,我打算包含一些处理时间和保存算法的信息。
虽然我们的机器学习分类器花费几秒来训练,在一些情况下,训练分类器需要几个小时甚至是几天。想象你想要预测价格的每天都需要这么做。这不是必要的,因为我们呢可以使用
Pickle 模块来保存分类器。首先确保你导入了它:
使用 Pickle,你可以保存 Python 对象,就像我们的分类器那样。在定义、训练和测试你的分类器之后,添加:
| with
open('linearregression.pickle','wb') as f:
pickle.dump(clf, f) |
现在,再次执行脚本,你应该得到了linearregression.pickle,它是分类器的序列化数据。现在,你需要做的所有事情就是加载pickle文件,将其保存到clf,并照常使用,例如:
| pickle_in
= open('linearregression.pickle','rb')
clf = pickle.load(pickle_in) |
代码中:
| import
Quandl, math
import numpy as np
import pandas as pd
from sklearn import preprocessing, cross_validation,
svm
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
from matplotlib import style
import datetime
import pickle
style.use('ggplot')
df = Quandl.get("WIKI/GOOGL")
df = df[['Adj. Open', 'Adj. High', 'Adj. Low',
'Adj. Close', 'Adj. Volume']]
df['HL_PCT'] = (df['Adj. High'] - df['Adj. Low'])
/ df['Adj. Close'] * 100.0
df['PCT_change'] = (df['Adj. Close'] - df['Adj.
Open']) / df['Adj. Open'] * 100.0
df = df[['Adj. Close', 'HL_PCT', 'PCT_change',
'Adj. Volume']]
forecast_col = 'Adj. Close'
df.fillna(value=-99999, inplace=True)
forecast_out = int(math.ceil(0.1 * len(df)))
df['label'] = df[forecast_col].shift(-forecast_out)
X = np.array(df.drop(['label'], 1))
X = preprocessing.scale(X)
X_lately = X[-forecast_out:]
X = X[:-forecast_out]
df.dropna(inplace=True)
y = np.array(df['label'])
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X,
y, test_size=0.2)
#COMMENTED OUT:
##clf = svm.SVR(kernel='linear')
##clf.fit(X_train, y_train)
##confidence = clf.score(X_test, y_test)
##print(confidence)
pickle_in = open('linearregression.pickle','rb')
clf = pickle.load(pickle_in)
forecast_set = clf.predict(X_lately)
df['Forecast'] = np.nan
last_date = df.iloc[-1].name
last_unix = last_date.timestamp()
one_day = 86400
next_unix = last_unix + one_day
for i in forecast_set:
next_date = datetime.datetime.fromtimestamp(next_unix)
next_unix += 86400
df.loc[next_date] = [np.nan for _ in range(len(df.columns)-1)]+[i]
df['Adj. Close'].plot()
df['Forecast'].plot()
plt.legend(loc=4)
plt.xlabel('Date')
plt.ylabel('Price')
plt.show() |
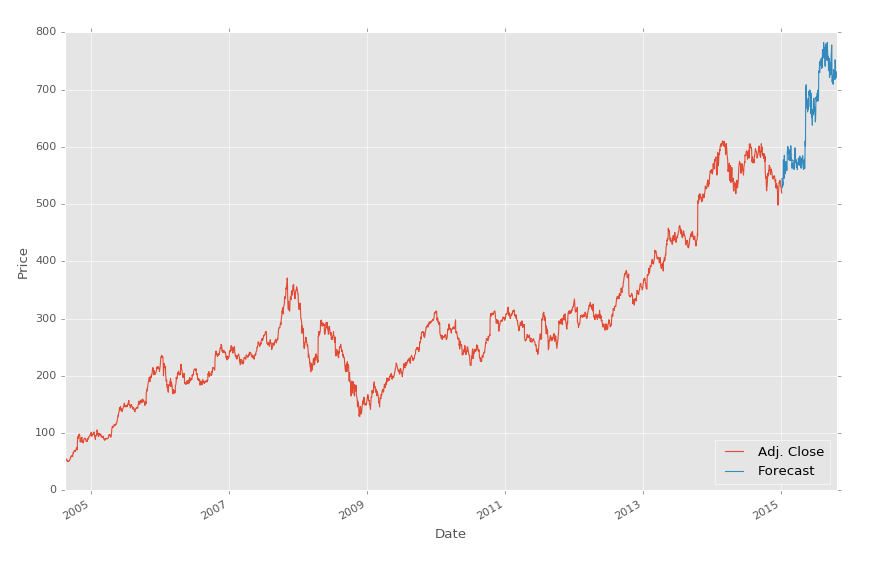
要注意我们注释掉了分类器的原始定义,并替换为加载我们保存的分类器。就是这么简单。
最后,我们要讨论一下效率和保存时间,前几天我打算提出一个相对较低的范式,这就是临时的超级计算机。严肃地说,随着按需主机服务的兴起,例如
AWS、DO 和 Linode,你能够按照小时来购买主机。虚拟服务器可以在 60 秒内建立,所需的模块可以在
15 分钟内安装,所以非常有限。你可以写一个 shell 脚本或者什么东西来给它加速。考虑你需要大量的处理,并且还没有一台顶级计算机,或者你使用笔记本。没有问题,只需要启动一台服务器。
我对这个方式的最后一个注解是,使用任何主机,你通常都可以建立一个非常小型的服务器,加载所需的东西,之后扩展这个服务器。我喜欢以一个小型服务器开始,之后,我准备好的时候,我会改变它的尺寸,给它升级。完成之后,不要忘了注销或者降级你的服务器。
理论以及工作原理
欢迎阅读第七篇教程。目前为止,你已经看到了线性回归的价值,以及如何使用 Sklearn 来应用它。现在我们打算深入了解它如何计算。虽然我觉得不必要深入到每个机器学习算法数学中(你有没有进入到你最喜欢的模块的源码中,看看它是如何实现的?),线性代数是机器学习的本质,并且对于理解机器学习的构建基础十分实用。
线性代数的目标是计算向量空间中的点的关系。这可以用于很多事情,但是某天,有个人有了个非常狂野的想法,拿他处理数据集的特征。我们也可以。记得之前我们定义数据类型的时候,线性回归处理连续数据吗?这并不是因为使用线性回归的人,而是因为组成它的数学。简单的线性回归可用于寻找数据集的最佳拟合直线。如果数据不是连续的,就不是最佳拟合直线。让我们看看一些示例。
协方差
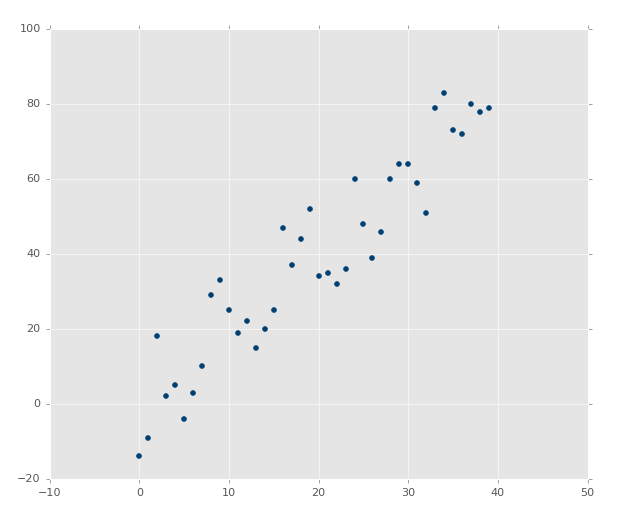
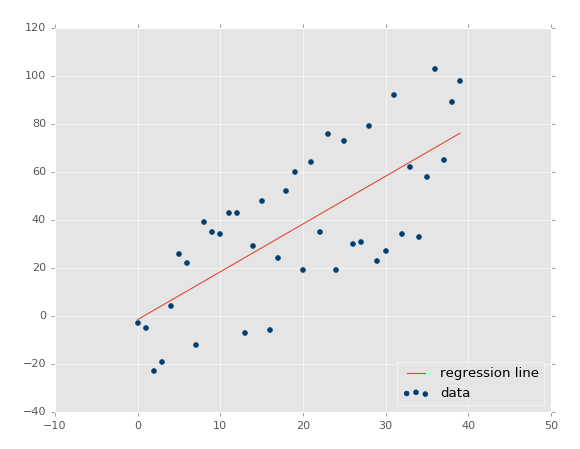
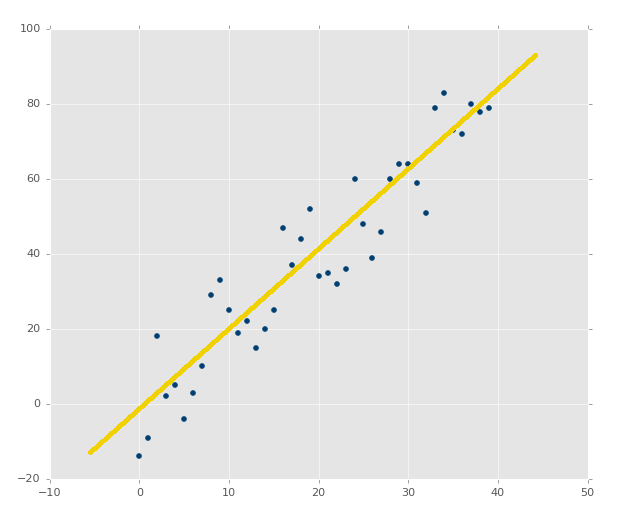
上面的图像显然拥有良好的协方差。如果你通过估计画一条最佳拟合直线,你应该能够轻易画出来:
如果图像是这样呢?
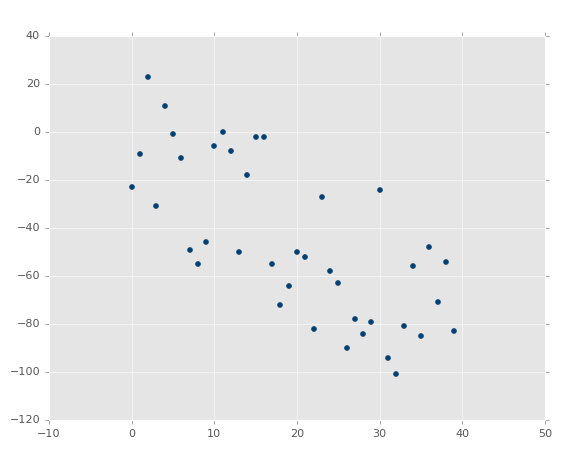
并不和之前一样,但是是清楚的负相关。你可能能够画出最佳拟合直线,但是更可能画不出来。
最后,这个呢?
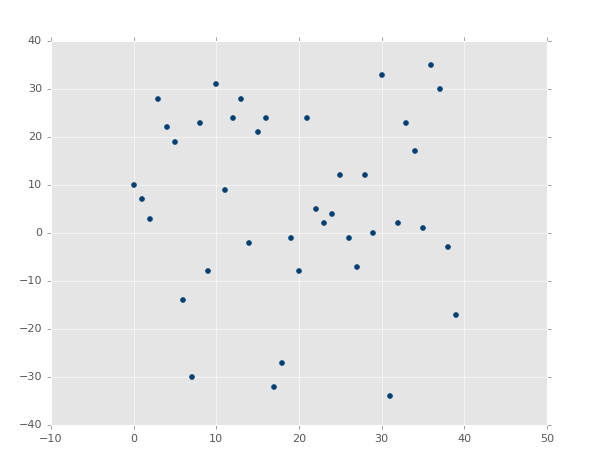
啥?的确有最佳拟合直线,但是需要运气将其画出来。
将上面的图像看做特征的图像,所以 X 坐标是特征,Y 坐标是相关的标签。X 和 Y 是否有任何形式的结构化关系呢?虽然我们可以准确计算关系,未来我们就不太可能拥有这么多值了。
在其它图像的案例中,X 和 Y 之间显然存在关系。我们实际上可以探索这种关系,之后沿着我们希望的任何点绘图。我们可以拿
Y 来预测 X,或者拿 X 来预测 Y,对于任何我们可以想到的点。我们也可以预测我们的模型有多少的误差,即使模型只有一个点。我们如何实现这个魔法呢?当然是线性代数。
首先,让我们回到中学,我们在那里复习直线的定义:y = mx + b,其中m是斜率,b是纵截距。这可以是用于求解y的方程,我们可以将其变形来求解x,使用基本的代数原则:x
= (y-b)/m。
好的,所以,我们的目标是寻找最佳拟合直线。不是仅仅是拟合良好的直线,而是最好的那条。这条直线的定义就是y
= mx + b。y就是答案(我们其他的坐标,或者甚至是我们的特征),所以我们仍然需要m(斜率)和b(纵截距),由于x可能为沿
x 轴的任一点,所以它是已知的。
最佳拟合直线的斜率m定义为:
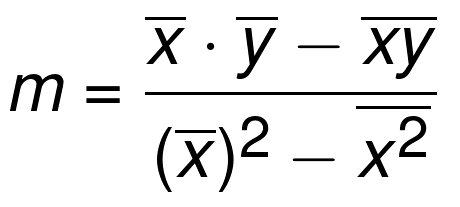
注:可简写为m = cov(x, y) / var(x)。
符号上面的横杠代表均值。如果两个符号挨着,就将其相乘。xs 和 ys
是所有已知坐标。所以我们现在求出了y=mx+b最佳拟合直线定义的m(斜率),现在我们仅仅需要b(纵截距)。这里是公式:
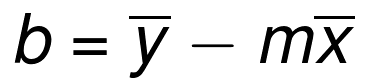
好的。整个部分不是个数学教程,而是个编程教程。下一个教程中,我们打算这样做,并且解释为什么我要编程实现它,而不是直接用模块。
编程计算斜率
欢迎阅读第八篇教程,我们刚刚意识到,我们需要使用 Python 重复编写一些比较重要的算法,来尝试给定数据集的计算最佳拟合直线。
在我们开始之前,为什么我们会有一些小麻烦呢?线性回归是机器学习的构建基础。它几乎用于每个单独的主流机器学习算法之中,所以对它的理解有助于你掌握多数主流机器学习算法。出于我们的热情,理解线性回归和线性代数,是编写你自己的机器学习算法,以及跨入机器学习前沿,使用当前最佳的处理过程的第一步。由于处理过程的优化和硬件架构的改变。用于机器学习的方法论也会改变。最近出现的神经网络,使用大量
GPU 来完成工作。你想知道什么是神经网络的核心吗?你猜对了,线性代数。
如果你能记得,最佳拟合直线的斜率m:
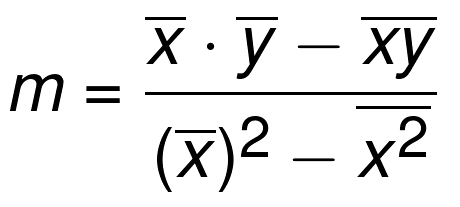
是的,我们会将其拆成片段。首先,进行一些导入:
| from
statistics import mean
import numpy as np |
我们从statistics导入mean,所以我们可以轻易获取列表的均值。下面,我们使numpy
as np,所以我们可以其创建 NumPy 数组。我们可以对列表做很多事情,但是我们需要能够做一些简单的矩阵运算,它并不对简单列表提供,所以我们使用
NumPy。我们在这个阶段不会使用太复杂的 NumPy,但是之后 NumPy 就会成为你的最佳伙伴。下面,让我们定义一些起始点吧。
| xs
= [1,2,3,4,5]
ys = [5,4,6,5,6] |
所以这里有一些我们要使用的数据点,xs和ys。你可以认为xs就是特征,ys就是标签,或者他们都是特征,我们想要建立他们的联系。之前提到过,我们实际上把它们变成
NumPy 数组,以便执行矩阵运算。所以让我们修改这两行:
| xs
= np.array([1,2,3,4,5], dtype=np.float64)
ys = np.array([5,4,6,5,6], dtype=np.float64) |
现在他们都是 NumPy 数组了。我们也显式声明了数据类型。简单讲一下,数据类型有特性是属性,这些属性决定了数据本身如何储存和操作。现在它不是什么问题,但是如果我们执行大量运算,并希望他们跑在
GPU 而不是 CPU 上就是了。
将其画出来,他们是:

现在我们准备好构建函数来计算m,也就是我们的直线斜率:
| def
best_fit_slope(xs,ys):
return m
m = best_fit_slope(xs,ys) |
好了。开个玩笑,所以这是我们的框架,现在我们要填充了。
我们的第一个逻辑就是计算xs的均值,再乘上ys的均值。继续填充我们的框架:
| def
best_fit_slope(xs,ys):
m = (mean(xs) * mean(ys))
return m |
目前为止还很简单。你可以对列表、元组或者数组使用mean函数。要注意我这里使用了括号。Python
的遵循运算符的数学优先级。所以如果你打算保证顺序,要显式使用括号。要记住你的运算规则。
下面我们需要将其减去x*y的均值。这既是我们的矩阵运算mean(xs*ys)。现在的代码是:
| def
best_fit_slope(xs,ys):
m = ( (mean(xs)*mean(ys)) - mean(xs*ys) )
return m |
我们完成了公式的分子部分,现在我们继续处理的分母,以x的均值平方开始:(mean(xs)*mean(xs))。Python
支持** 2,能够处理我们的 NumPy 数组的float64类型。添加这些东西:
| def
best_fit_slope(xs,ys):
m = ( ((mean(xs)*mean(ys)) - mean(xs*ys)) /
(mean(xs)**2))
return m |
虽然根据运算符优先级,向整个表达式添加括号是不必要的。我这里这样做,所以我可以在除法后面添加一行,使整个式子更加易读和易理解。不这样的话,我们会在新的一行得到语法错误。我们几乎完成了,现在我们只需要将x的均值平方和x的平方均值(mean(xs*xs))相减。全部代码为:
| def
best_fit_slope(xs,ys):
m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
((mean(xs)**2) - mean(xs*xs)))
return m |
好的,现在我们的完整脚本为:
| from
statistics import mean
import numpy as np
xs = np.array([1,2,3,4,5], dtype=np.float64)
ys = np.array([5,4,6,5,6], dtype=np.float64)
def best_fit_slope(xs,ys):
m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
((mean(xs)**2) - mean(xs**2)))
return m
m = best_fit_slope(xs,ys)
print(m)
# 0.3 |
下面干什么?我们需要计算纵截距b。我们会在下一个教程中处理它,并完成完整的最佳拟合直线计算。它比斜率更佳易于计算,尝试编写你自己的函数来计算它。如果你做到了,也不要跳过下一个教程,我们会做一些别的事情。
计算纵截距
欢迎阅读第九篇教程。我们当前正在为给定的数据集,使用 Python
计算回归或者最佳拟合直线。之前,我们编写了一个函数来计算斜率,现在我们需要计算纵截距。我们目前的代码是:
| from
statistics import mean
import numpy as np
xs = np.array([1,2,3,4,5], dtype=np.float64)
ys = np.array([5,4,6,5,6], dtype=np.float64)
def best_fit_slope(xs,ys):
m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
((mean(xs)*mean(xs)) - mean(xs*xs)))
return m
m = best_fit_slope(xs,ys)
print(m) |
请回忆,最佳拟合直线的纵截距是:
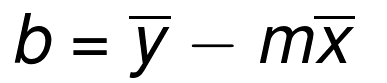
这个比斜率简单多了。我们可以将其写到同一个函数来节省几行代码。我们将函数重命名为best_fit_slope_and_intercept。
下面,我们可以填充b = mean(ys) - (m*mean(xs)),并返回m, b:
| def
best_fit_slope_and_intercept(xs,ys):
m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
((mean(xs)*mean(xs)) - mean(xs*xs)))
b = mean(ys) - m*mean(xs)
return m, b |
现在我们可以调用它:
| best_fit_slope_and_intercept(xs,ys) |
我们目前为止的代码:
| from
statistics import mean
import numpy as np
xs = np.array([1,2,3,4,5], dtype=np.float64)
ys = np.array([5,4,6,5,6], dtype=np.float64)
def best_fit_slope_and_intercept(xs,ys):
m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
((mean(xs)*mean(xs)) - mean(xs*xs)))
b = mean(ys) - m*mean(xs)
return m, b
m, b = best_fit_slope_and_intercept(xs,ys)
print(m,b)
# 0.3, 4.3 |
现在我们仅仅需要为数据创建一条直线:

要记住y=mx+b,我们能够为此编写一个函数,或者仅仅使用一行的for循环。
| regression_line
= [(m*x)+b for x in xs] |
上面的一行for循环和这个相同:
| regression_line
= []
for x in xs:
regression_line.append((m*x)+b) |
好的,让我们收取我们的劳动果实吧。添加下面的导入:
| import
matplotlib.pyplot as plt
from matplotlib import style
style.use('ggplot') |
我们可以绘制图像,并且不会特备难看。现在:
| plt.scatter(xs,ys,color='#003F72')
plt.plot(xs, regression_line)
plt.show() |
首先我们绘制了现有数据的散点图,之后我们绘制了我们的回归直线,之后展示它。如果你不熟悉,可以查看 Matplotlib
教程集。
输出:
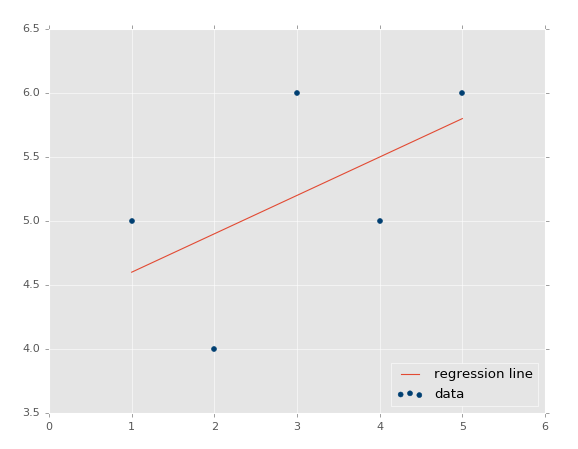
恭喜恭喜。所以,如何基础这个模型来做一些实际的预测呢?很简单,你拥有了模型,只要填充x就行了。例如,让我们预测一些点:
我们输入了数据,也就是我们的特征。那么标签呢?
| predict_y
= (m*predict_x)+b
print(predict_y)
# 6.4 |
我们也可以绘制它:
| predict_x
= 7
predict_y = (m*predict_x)+b
plt.scatter(xs,ys,color='#003F72',label='data')
plt.plot(xs, regression_line, label='regression
line')
plt.legend(loc=4)
plt.show() |
输出:
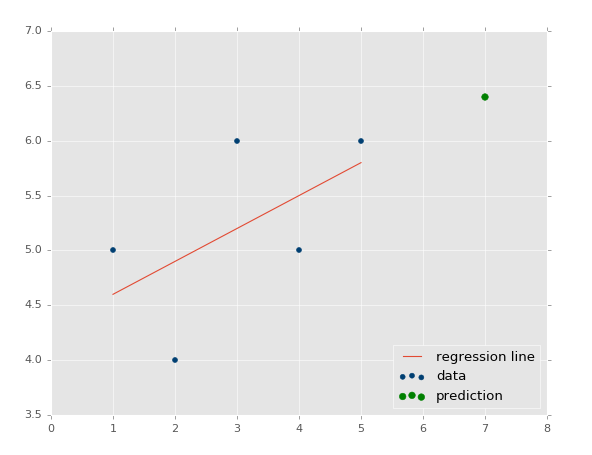
我们现在知道了如何创建自己的模型,这很好,但是我们仍旧缺少了一些东西,我们的模型有多精确?这就是下一个教程的话题了。
R 平方和判定系数原理
欢迎阅读第十篇教程。我们刚刚完成了线性模型的创建和处理,现在我们好奇接下来要干什么。现在,我们可以轻易观察数,并决定线性回归模型有多么准确。但是,如果你的线性回归模型是拿神经网络的
20 个层级做出来的呢?不仅仅是这样,你的模型以步骤或者窗口工作,也就是一共 5 百万个数据点,一次只显示
100 个,会怎么样?你需要一些自动化的方式来判断你的最佳拟合直线有多好。
回忆之前,我们展示几个绘图的时候,你已经看到,最佳拟合直线好还是不好。像这样:
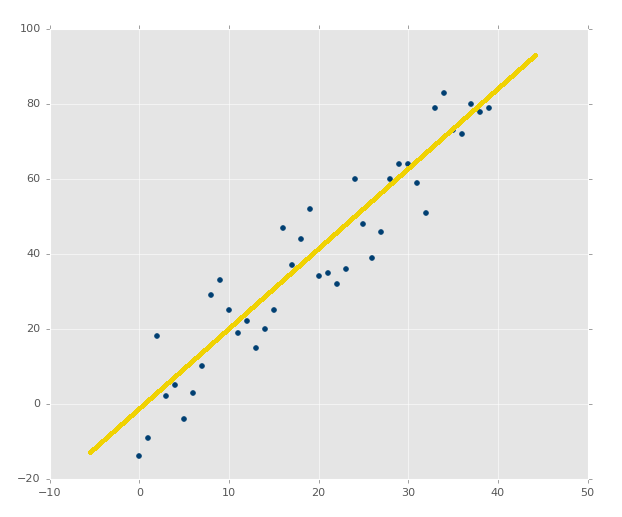
与这个相比:
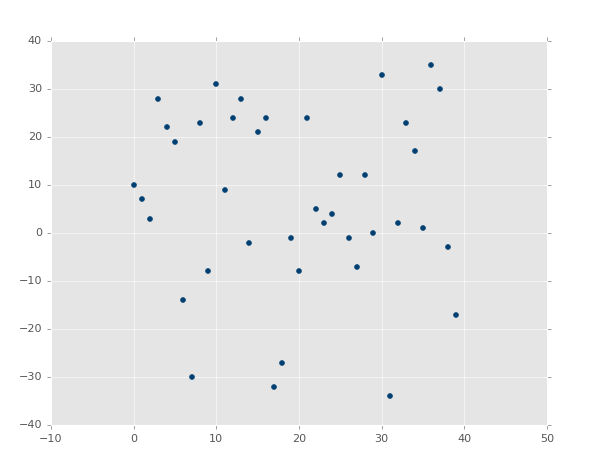
第二张图片中,的确有最佳拟合直线,但是没有人在意。即使是最佳拟合直线也是没有用的。并且,我们想在花费大量计算能力之前就知道它。
检查误差的标准方式就是使用平方误差。你可能之前听说过,这个方法叫做
R 平方或者判定系数。什么叫平方误差呢?
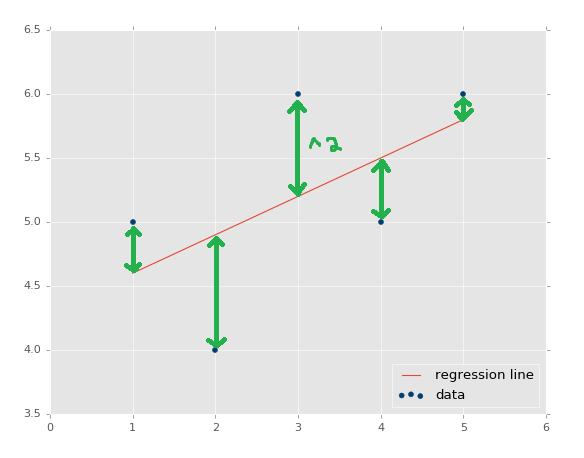
回归直线和数据的y值的距离,就叫做误差,我们将其平方。直线的平方误差是它们的平均或者和。我们简单求和吧。
我们实际上已经解除了平方误差假设。我们的最佳拟合直线方程,用于计算最佳拟合回归直线,就是证明结果。其中回归直线就是拥有最小平方误差的直线(所以它才叫做最小二乘法)。你可以搜索“回归证明”,或者“最佳拟合直线证明”来理解它。它很抑郁理解,但是需要代数变形能力来得出结果。
为啥是平方误差?为什么不仅仅将其加起来?首先,我们想要一种方式,将误差规范化为距离,所以误差可能是
-5,但是,平方之后,它就是正数了。另一个原因是要进一步惩罚离群点。进一步的意思是,它影响误差的程度更大。这就是人们所使用的标准方式。你也可以使用4,
6, 8的幂,或者其他。你也可以仅仅使用误差的绝对值。如果你只有一个挑战,也许就是存在一些离群点,但是你并不打算管它们,你就可以考虑使用绝对值。如果你比较在意离群点,你就可以使用更高阶的指数。我们会使用平方,因为这是大多数人所使用的。
好的,所以我们计算回归直线的平方误差,什么计算呢?这是什么意思?平方误差完全和数据集相关,所以我们不再需要别的东西了。这就是
R 平方引入的时候了,也叫作判定系数。方程是:
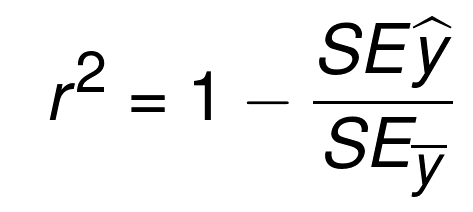
| y_hat
= x * m + b
r_sq = 1 - np.sum((y - y_hat) ** 2) / np.sum((y
- y.mean()) ** 2) |
这个方程的的本质就是,1 减去回归直线的平方误差,比上 y 平均直线的平方误差。 y 平均直线就是数据集中所有
y 值的均值,如果你将其画出来,它是一个水平的直线。所以,我们计算 y 平均直线,和回归直线的平方误差。这里的目标是识别,与欠拟合的直线相比,数据特征的变化产生了多少误差。
所以判定系数就是上面那个方程,如何判定它是好是坏?我们看到了它是 1 减去一些东西。通常,在数学中,你看到他的时候,它返回了一个百分比,它是
0 ~ 1 之间的数值。你认为什么是好的 R 平方或者判定系数呢?让我们假设这里的 R 平方是 0.8,它是好是坏呢?它比
0.3 是好还是坏?对于 0.8 的 R 平方,这就意味着回归直线的平方误差,比上 y 均值的平方误差是
2 比 10。这就是说回归直线的误差非常小于 y 均值的误差。听起来不错。所以 0.8 非常好。
那么与判定系数的值 0.3 相比呢?这里,它意味着回归直线的平方误差,比上 y 均值的平方误差是
7 比 10。其中 7 比 10 要坏于 2 比 10,7 和 2 都是回归直线的平方误差。因此,目标是计算
R 平方值,或者叫做判定系数,使其尽量接近 1。
编程计算 R 平方
欢迎阅读第十一篇教程。既然我们知道了我们寻找的东西,让我们实际在 Python 中计算它吧。第一步就是计算平方误差。函数可能是这样:
| def
squared_error(ys_orig,ys_line):
return sum((ys_line - ys_orig) * (ys_line -
ys_orig)) |
使用上面的函数,我们可以计算出任何实现到数据点的平方误差。所以我们可以将这个语法用于回归直线和 y
均值直线。也就是说,平方误差只是判定系数的一部分,所以让我们构建那个函数吧。由于平方误差函数只有一行,你可以选择将其嵌入到判定系数函数中,但是平方误差是你在这个函数之外计算的东西,所以我选择将其单独写成一个函数。对于
R 平方:
| def
coefficient_of_determination(ys_orig,ys_line):
y_mean_line = [mean(ys_orig) for y in ys_orig]
squared_error_regr = squared_error(ys_orig,
ys_line)
squared_error_y_mean = squared_error(ys_orig,
y_mean_line)
return 1 - (squared_error_regr/squared_error_y_mean) |
我们所做的是,计算 y 均值直线,使用单行的for循环(其实是不必要的)。之后我们计算了 y 均值的平方误差,以及回归直线的平方误差,使用上面的函数。现在,我们需要做的就是计算出
R 平方之,它仅仅是 1 减去回归直线的平方误差,除以 y 均值直线的平方误差。我们返回该值,然后就完成了。组合起来并跳过绘图部分,代码为:
| from
statistics import mean
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
style.use('ggplot')
xs = np.array([1,2,3,4,5], dtype=np.float64)
ys = np.array([5,4,6,5,6], dtype=np.float64)
def best_fit_slope_and_intercept(xs,ys):
m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
((mean(xs)*mean(xs)) - mean(xs*xs)))
b = mean(ys) - m*mean(xs)
return m, b
def squared_error(ys_orig,ys_line):
return sum((ys_line - ys_orig) * (ys_line -
ys_orig))
def coefficient_of_determination(ys_orig,ys_line):
y_mean_line = [mean(ys_orig) for y in ys_orig]
squared_error_regr = squared_error(ys_orig,
ys_line)
squared_error_y_mean = squared_error(ys_orig,
y_mean_line)
return 1 - (squared_error_regr/squared_error_y_mean)
m, b = best_fit_slope_and_intercept(xs,ys)
regression_line = [(m*x)+b for x in xs]
r_squared = coefficient_of_determination(ys,regression_line)
print(r_squared)
# 0.321428571429
##plt.scatter(xs,ys,color='#003F72',label='data')
##plt.plot(xs, regression_line, label='regression
line')
##plt.legend(loc=4)
##plt.show() |
这是个很低的值,所以根据这个度量,我们的最佳拟合直线并不是很好。这里的 R 平方是个很好的度量手段吗?可能取决于我们的目标。多数情况下,如果我们关心准确预测未来的值,R
平方的确很有用。如果你对预测动机或者趋势感兴趣,我们的最佳拟合直线实际上已经很好了。R 平方不应该如此重要。看一看我们实际的数据集,我们被一个较低的数值卡住了。值与值之间的变化在某些点上是
20% ~ 50%,这已经非常高了。我们完全不应该感到意外,使用这个简单的数据集,我们的最佳拟合直线并不能描述真实数据。
但是,我们刚才说的是一个假设。虽然我们逻辑上统一这个假设,我们需要提出一个新的方法,来验证假设。到目前为止的算法非常基础,我们现在只能做很少的事情,所以没有什么空间来改进误差了,但是之后,你会在空间之上发现空间。不仅仅要考虑算法本身的层次空间,还有由很多算法层次组合而成的算法。其中,我们需要测试它们来确保我们的假设,关于算法是干什么用的,是正确的。考虑把操作组成成函数由多么简单,之后,从这里开始,将整个验证分解成数千行代码。
我们在下一篇教程所做的是,构建一个相对简单的数据集生成器,根据我们的参数来生成数据。我们可以使用它来按照意愿操作数据,之后对这些数据集测试我们的算法,根据我们的假设修改参数,应该会产生一些影响。我们之后可以将我们的假设和真实情况比较,并希望他们匹配。这里的例子中,假设是我们正确编写这些算法,并且判定系数低的原因是,y
值的方差太大了。我们会在下一个教程中验证这个假设。
为测试创建样例数据集
欢迎阅读第十二篇教程。我们已经了解了回归,甚至编写了我们自己的简单线性回归算法。并且,我们也构建了判定系数算法来检查最佳拟合直线的准确度和可靠性。我们之前讨论和展示过,最佳拟合直线可能不是最好的拟合,也解释了为什么我们的示例方向上是正确的,即使并不准确。但是现在,我们使用两个顶级算法,它们由一些小型算法组成。随着我们继续构造这种算法层次,如果它们之中有个小错误,我们就会遇到麻烦,所以我们打算验证我们的假设。
在编程的世界中,系统化的程序测试通常叫做“单元测试”。这就是大型程序构建的方式,每个小型的子系统都不断检查。随着大型程序的升级和更新,可以轻易移除一些和之前系统冲突的工具。使用机器学习,这也是个问题,但是我们的主要关注点仅仅是测试我们的假设。最后,你应该足够聪明,可以为你的整个机器学习系统创建单元测试,但是目前为止,我们需要尽可能简单。
我们的假设是,我们创建了最贱he直线,之后使用判定系数法来测量。我们知道(数学上),R 平方的值越低,最佳拟合直线就越不好,并且越高(接近
1)就越好。我们的假设是,我们构建了一个这样工作的系统,我们的系统有许多部分,即使是一个小的操作错误都会产生很大的麻烦。我们如何测试算法的行为,保证任何东西都预期工作呢?
这里的理念是创建一个样例数据集,由我们定义,如果我们有一个正相关的数据集,相关性非常强,如果相关性很弱的话,点也不是很紧密。我们用眼睛很容易评测这个直线,但是机器应该做得更好。让我们构建一个系统,生成示例数据,我们可以调整这些参数。
最开始,我们构建一个框架函数,模拟我们的最终目标:
| def
create_dataset(hm,variance,step=2,correlation=False):
return np.array(xs, dtype=np.float64),np.array(ys,dtype=np.float64) |
我们查看函数的开头,它接受下列参数:
1.hm(how much):这是生成多少个数据点。例如我们可以选择
10,或者一千万。
2.variance:决定每个数据点和之前的数据点相比,有多大变化。变化越大,就越不紧密。
3.step:每个点距离均值有多远,默认为 2。
4.correlation:可以为False、pos或者neg,决定不相关、正相关和负相关。
要注意,我们也导入了random,这会帮助我们生成(伪)随机数据集。
现在我们要开始填充函数了。
| def
create_dataset(hm,variance,step=2,correlation=False):
val = 1
ys = []
for i in range(hm):
y = val + random.randrange(-variance,variance)
ys.append(y) |
非常简单,我们仅仅使用hm变量,迭代我们所选的范围,将当前值加上一个负差值到证差值的随机范围。这会产生数据,但是如果我们想要的话,它没有相关性。让我们这样:
| def
create_dataset(hm,variance,step=2,correlation=False):
val = 1
ys = []
for i in range(hm):
y = val + random.randrange(-variance,variance)
ys.append(y)
if correlation and correlation == 'pos':
val+=step
elif correlation and correlation == 'neg':
val-=step |
非常棒了,现在我们定义好了 y 值。下面,让我们创建 x,它更简单,只是返回所有东西。
| def
create_dataset(hm,variance,step=2,correlation=False):
val = 1
ys = []
for i in range(hm):
y = val + random.randrange(-variance,variance)
ys.append(y)
if correlation and correlation == 'pos':
val+=step
elif correlation and correlation == 'neg':
val-=step
xs = [i for i in range(len(ys))]
return np.array(xs, dtype=np.float64),np.array(ys,dtype=np.float64) |
我们准备好了。为了创建样例数据集,我们所需的就是:
| xs,
ys = create_dataset(40,40,2,correlation='pos') |
让我们将之前线性回归教程的代码放到一起:
| from
statistics import mean
import numpy as np
import random
import matplotlib.pyplot as plt
from matplotlib import style
style.use('ggplot')
def create_dataset(hm,variance,step=2,correlation=False):
val = 1
ys = []
for i in range(hm):
y = val + random.randrange(-variance,variance)
ys.append(y)
if correlation and correlation == 'pos':
val+=step
elif correlation and correlation == 'neg':
val-=step
xs = [i for i in range(len(ys))]
return np.array(xs, dtype=np.float64),np.array(ys,dtype=np.float64)
def best_fit_slope_and_intercept(xs,ys):
m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
((mean(xs)*mean(xs)) - mean(xs*xs)))
b = mean(ys) - m*mean(xs)
return m, b
def coefficient_of_determination(ys_orig,ys_line):
y_mean_line = [mean(ys_orig) for y in ys_orig]
squared_error_regr = sum((ys_line - ys_orig)
* (ys_line - ys_orig))
squared_error_y_mean = sum((y_mean_line - ys_orig)
* (y_mean_line - ys_orig))
print(squared_error_regr)
print(squared_error_y_mean)
r_squared = 1 - (squared_error_regr/squared_error_y_mean)
return r_squared
xs, ys = create_dataset(40,40,2,correlation='pos')
m, b = best_fit_slope_and_intercept(xs,ys)
regression_line = [(m*x)+b for x in xs]
r_squared = coefficient_of_determination(ys,regression_line)
print(r_squared)
plt.scatter(xs,ys,color='#003F72', label =
'data')
plt.plot(xs, regression_line, label = 'regression
line')
plt.legend(loc=4)
plt.show() |
执行代码,你会看到:
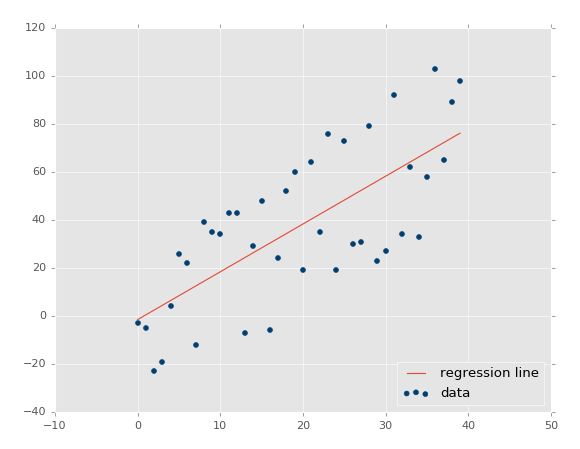
判定系数是 0.516508576011(要注意你的结果不会相同,因为我们使用了随机数范围)。
不错,所以我们的假设是,如果我们生成一个更加紧密相关的数据集,我们的
R 平方或判定系数应该更好。如何实现它呢?很简单,把范围调低。
| xs,
ys = create_dataset(40,10,2,correlation='pos') |
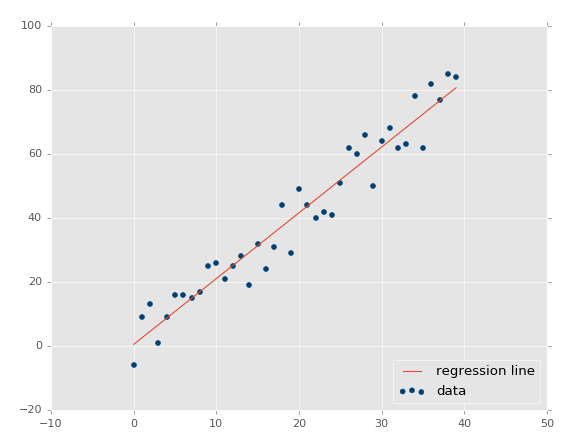
现在我们的 R 平方值为 0.939865240568,非常不错,就像预期一样。让我们测试负相关:
| xs,
ys = create_dataset(40,10,2,correlation='neg') |
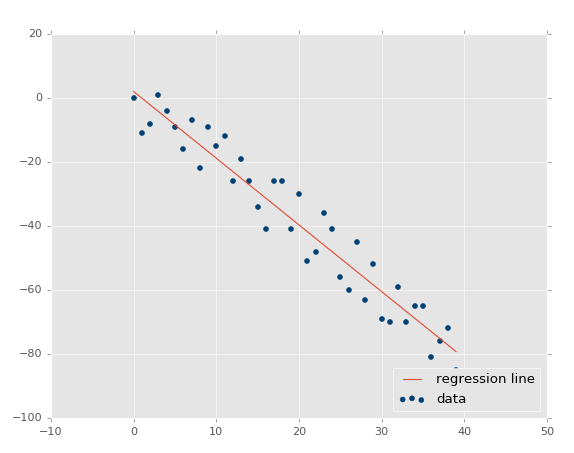
R 平方值是 0.930242442156,跟之前一样好,由于它们参数相同,只是方向不同。
这里,我们的假设证实了:变化越小 R 值和判定系数越高,变化越大
R 值越低。如果是不相关呢?应该很低,接近于 0,除非我们的随机数排列实际上有相关性。让我们测试:
| xs,
ys = create_dataset(40,10,2,correlation=False) |
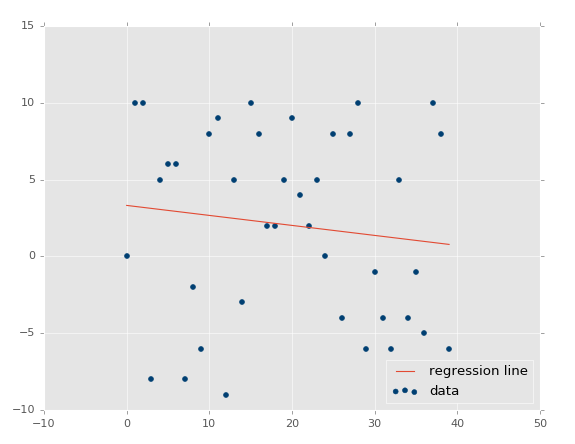
判定系数为 0.0152650900427。
现在为止,我觉得我们应该感到自信,因为事情都符合我们的预期。
既然我们已经对简单的线性回归很熟悉了,下个教程中我们开始讲解分类。
|