| 编辑推荐: |
| 本文来自于daniellaah.github.io,介绍了机器学习的单变量线性回归的模型展示中的函数和梯度,文中采用多数图片的形式详细描述。 |
|
本文的第一篇我的机器学习笔记(一)-监督学习vs
无监督学习
模型展示
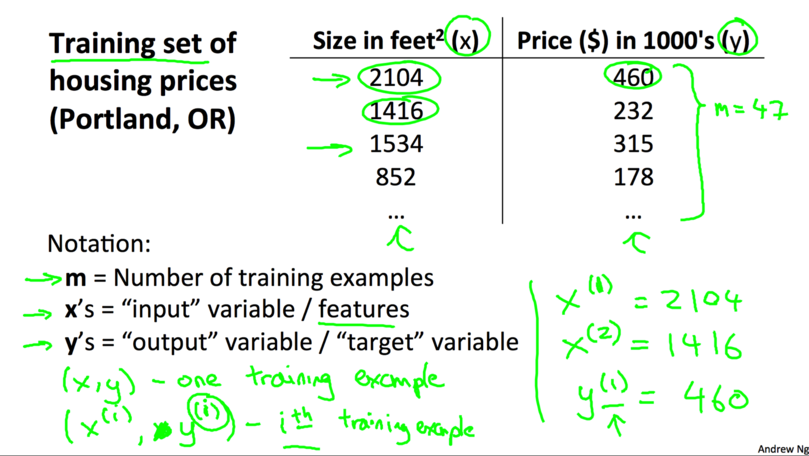
训练集
什么是训练集(Training Set)?有训练样例(training example)组成的集合就是训练集。如下图所示,右边的两列数据就是本例子中的训练集,
其中\((x, y)\)是一个训练样例,\((x^{(i)}, y^{(i)})\)是第\(i\)个训练样例。
假设函数
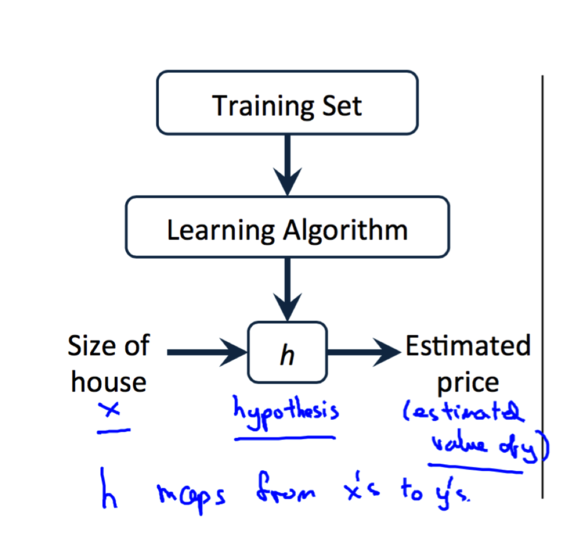
通过训练集和学习算法我们就可以得到假设函数(Hypothesis
Function),假设函数记为h。在房屋的例子中,我们的假设函数就相当于一个由房屋面积到房屋价格的近似函数,通过这个假设就可以得出相应面积房屋的估价了。如下图所示:
那么我们该如何表示假设函数呢?在本例中,只有一个变量x(房屋的面积),我们可以将假设函数h以如下的形式表示:<font
size='4'>$$ {h_\theta(x) =\theta_0+\theta_1x} $$</font>为了方便$h_\theta(x)$也可以记作$h(x)$。这个就叫做单变量的线性回归(Linear
Regression with One Variable)。(Linear regression with
one variable = Univariate linear regression, univariate是one
variable的装逼写法。) 如下图所示。

代价函数
在刚才的假设函数中有两个未知的参数$\theta_0$和$\theta_1$,当选择不同的$\theta_0$和$\theta_1$时,我们模型的效果肯定是不一样的。如下图所示,列举了三种情况下的假设函数。

那么我们该如何选择这两个参数呢?我们的想法是选择$\theta_0$和$\theta_1$,使得对于训练样例$(x,y)$,$h_\theta(x)$最接近$y$。即,使每个样例的估计值与真实值之间的差的平方的均值最小。用公式表达为:
<font size='4'>$${\mathop{minimize}\limits_{\theta_0,\theta_1}
\frac{1}{2m}\sum_{i=0}^m\left(h_\theta(x^{(i)}) -y^{(i)}\right)^2}$$</font>
将上面的公式minimize右边部分记为$J(\theta_0,\theta_1)$:
<font size='4'>$$ {J(\theta_0,\theta_1)
=\frac{1}{2m}\sum_{i=0} ^m\left(h_\theta(x^{(i)})-y^{(i)}\right)^2}$$</font>
这样就得到了我们的代价函数(Cost Function)$J (\theta_0,\theta_1)$,我们的目标就是<font
size='4'>$$\mathop{minimize} \limits_{\theta_0,\theta_1}
J(\theta_0,\theta_1)$$</font>

代价函数II
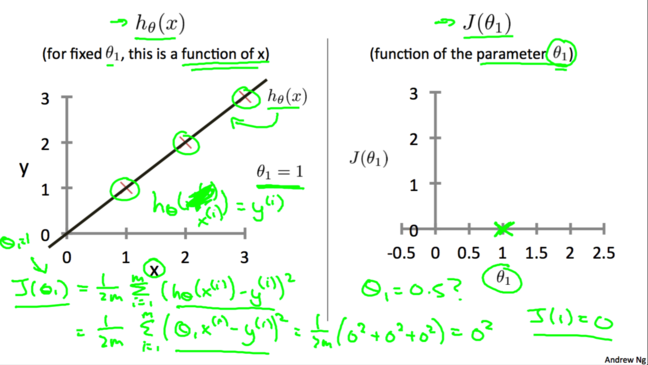
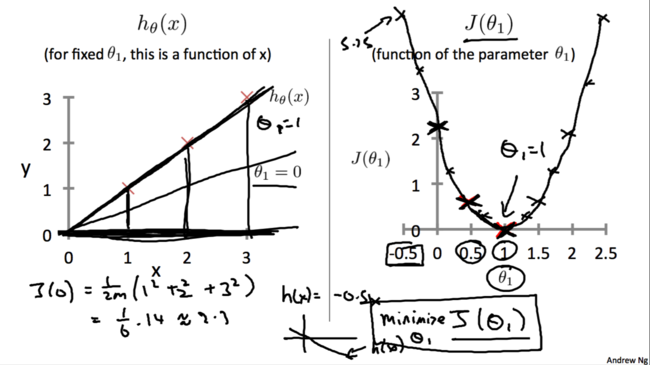
现在为了更方便地探究$h_\theta(x)$与$ J(\theta_0,\theta_1)$的关系,我们先令$\theta_0$等于0。这样我们就得到了简化后的假设函数,相应地也可以得到简化的代价函数。如图所示:

简化之后,我们再令$\theta_1=1$,就得到$h_\theta(x)=x$如下图左所示。图中三个红叉表示训练样例,通过代价函数的定义我们计算得出$J(1)=0$,对应下图右中的$(1,0)$坐标。
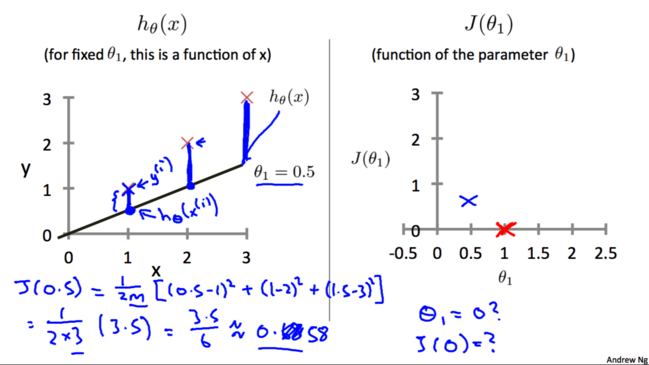
重复上面的步骤,再令$\theta_1=0.5$,得到$h_\theta(x)$如下图左所示。通过计算得出$J(0.5)=0.58$,对应下图右中的$(0.5,0.58)$坐标。
对于不同的$\theta_1$,可以得到不同的假设函数$h_\theta(x)$,于是就有了不同的$J(\theta_1)$的值。将这些点连接起来就可以得到$J(\theta_1)$的曲线,如下图所示:
代价函数III
在上一节中,我们令$\theta_0$等于0,得到$J(\theta_1)$的曲线。如果$\theta_0$不等于0,例如$\theta_0=50$,
$\theta_0=0.06$,此时就有两个变量,很容易想到$J(\theta_1)$应该是一个曲面。
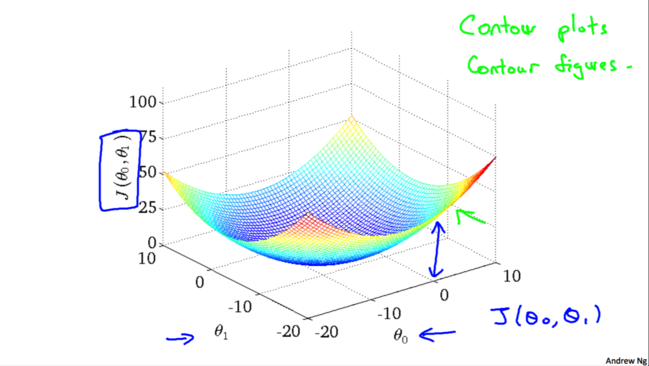
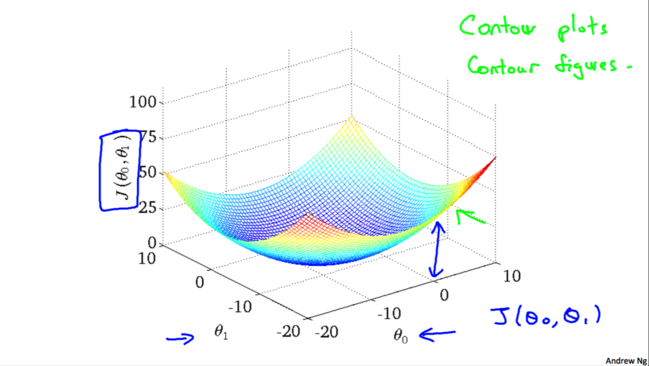
这个图是教授用matlab绘制的,由于3D图形不太方便我们研究,我们就使用二维的等高线(上图右上角教授写的contour
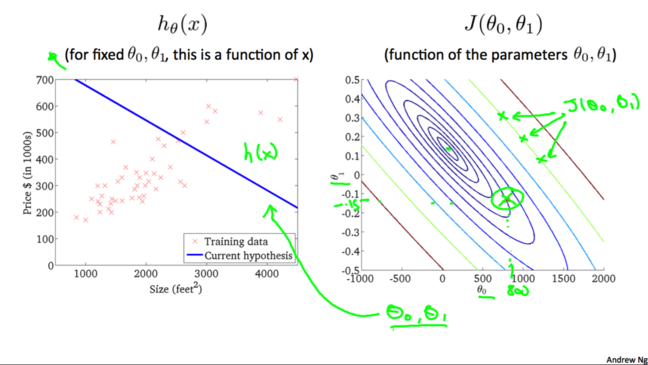
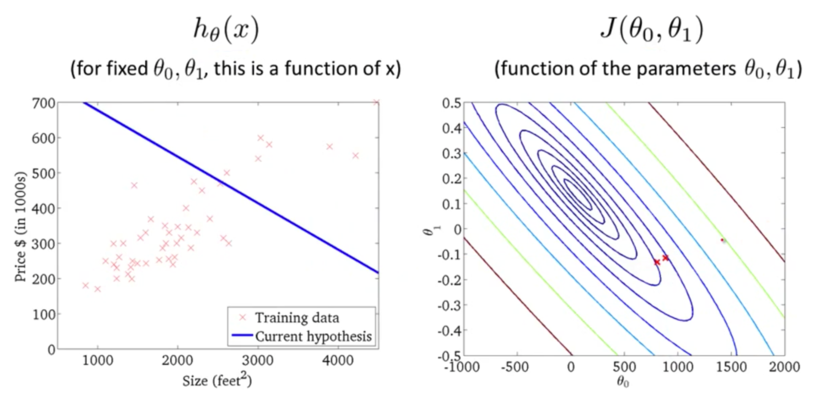
plots/figures),这样看上去比较清楚一些。如下图右,越往里表示$J(\theta_0,\theta_1)$的值越小(对应3D图中越靠近最低点的位置)。下图左表示当$\theta_0=800$,
$\theta_1=0.15$的时候对应的$h_\theta(x)$,通过$\theta_0$, $\theta_1$的值可以找到下图右中$J(\theta_0,\theta_1)$的值。
类似地:
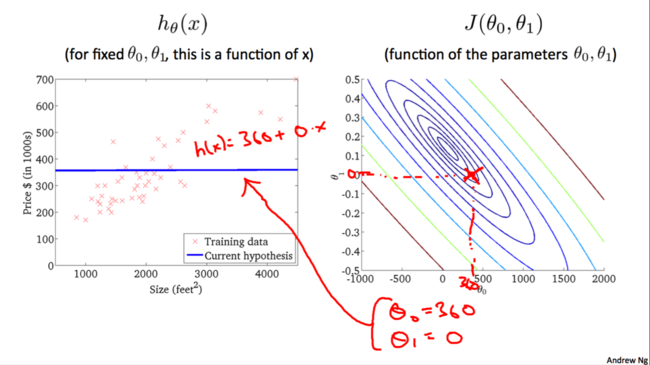
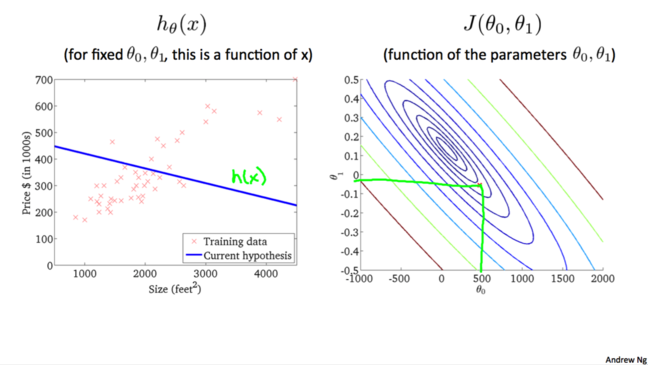
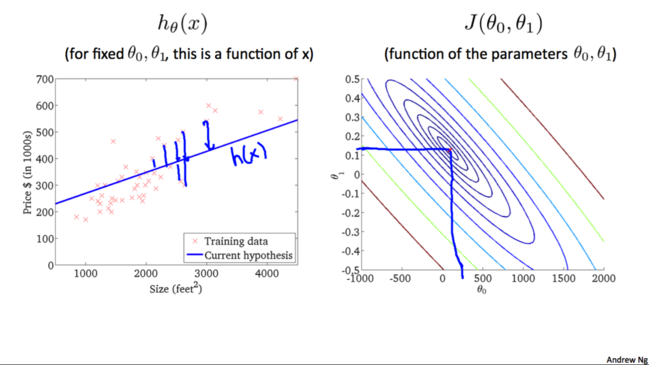
我们不断尝试直到找到一个最佳的$h_\theta(x)$,使得$J(\theta_0,\theta_1)$最小。当然我们不可能随机猜测或者手工尝试不同参数的值。我们能想到的应该就是通过设计程序,找到最佳的$h_\theta(x)$,也就是最合适的$\theta_0$和$\theta_1$。
梯度下降I
我们先直观的感受一下什么是梯度下降(Gradient Descent)。想要找到最合适的$\theta_0$和$\theta_1$,我们可以先以某一$\theta_0$和$\theta_1$开始,然后不断改变$\theta_0$和$\theta_1$的值使得$J(\theta_0,\theta_1)$值不断减小,直到找到一个最小值。

如下图所示,从某一点开始,每次沿着一定的梯度下降直到到达一个极小值为止。

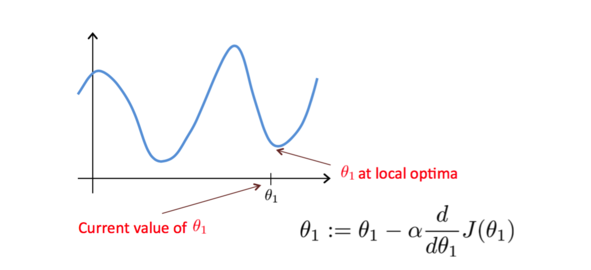
当从不同的点开始时(即不同的$\theta_0$和$\theta_1$),可能到达不同的最小值(极小值),如下图:
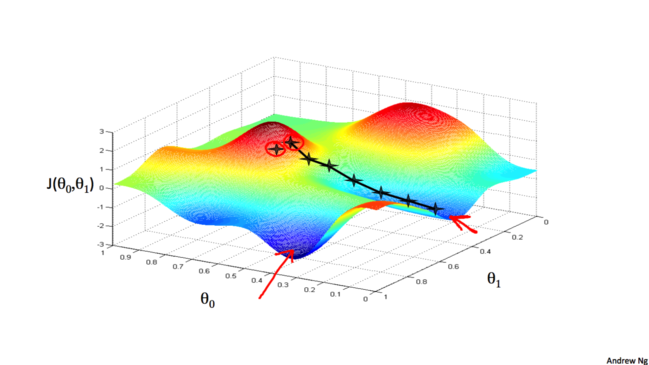
现在我们大概知道什么是梯度下降了,就好比下山一样,不同的山路有不同的坡度,有的山路走得快有的走得慢。一直往地处走有可能走到不同的最低点。那么我们每次该如何应该如何改变$\theta_0$和$\theta_1$的值呢?如下图所示,这里提到了梯度下降算法(Gradient
Descent Algorithm),其中$:=$表示赋值,$\alpha$叫做学习率,$\frac{\partial
}{\partial\theta_j}J(\theta_0, \theta_1)$叫做梯度。这里一定要注意的是,算法每次是同时(simultaneous)改变$\theta_0$和$\theta_1$的值,如图下图所示。

梯度下降II
现令$\theta_0$等于0,假设一开始选取的$\theta_1$在最低点的右侧,此时的梯度是一个正数。根据上面的算法更新$\theta_1$的时候,它的值会减小,即靠近最低点。
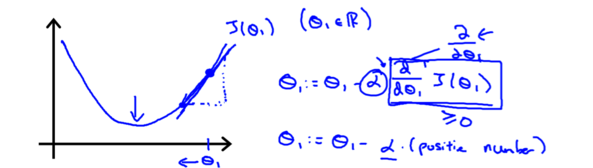
类似地假设一开始选取的$\theta_1$在最低点的左侧,此时的梯度是一个负数,根据上面的算法更新$\theta_1$的时候,它的值会增大,也会靠近最低点。
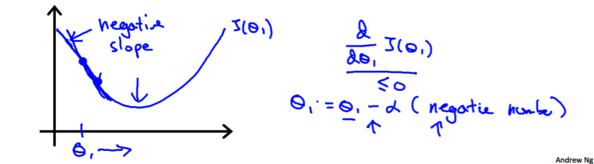
如果一开始选取的$\theta_1$恰好在最适位置,那么更新$\theta_1$时,它的值不会发生变化。
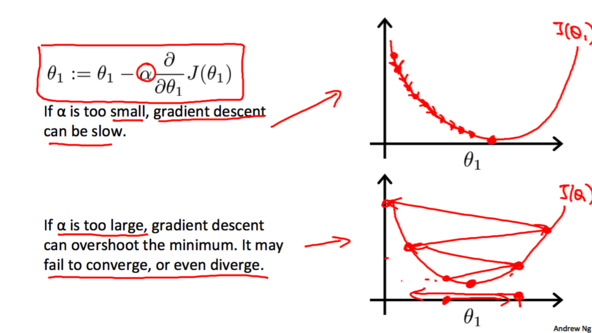
学习率$\alpha$会影响梯度下降的程度。如果$\alpha$太小,根据算法,$\theta$的值每次会变化的很小,那么梯度下降就会非常慢;相反地,如果$\alpha$过大,$\theta$的值每次会变化会很大,有可能直接越过最低点,可能导致永远没法到达最低点。
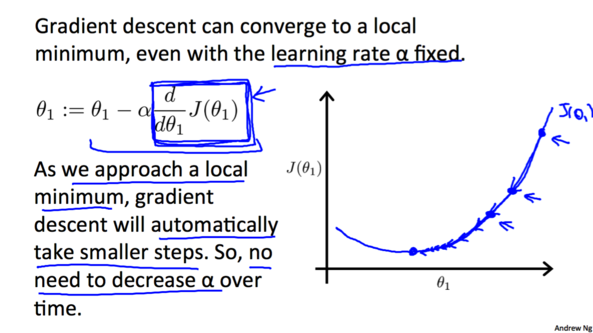
随着越来越接近最低点斜率(绝对值)会逐渐减小,每次下降程度就会越来越小。所以并不需要减小$\alpha$的值来减小下降程度。
梯度下降III
现在我们所要做的就是将梯度下降算法应用到线性回归模型中去,而其中最关键的就是计算其中的偏导数项,如下图所示。

我们将$h_\theta(x^{(i)})=\theta_0+\theta_1x^{(i)}$带入到$J(\theta_0,\theta_1)$中,并且分别对$\theta_0$和$\theta_1$求导得:
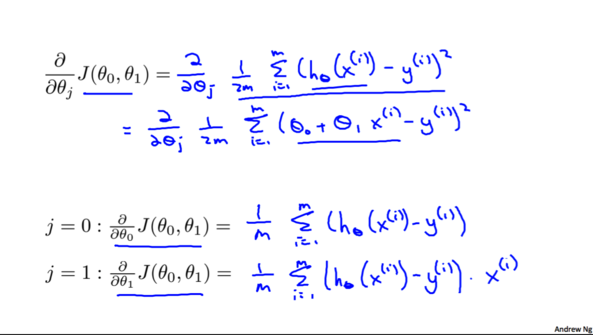
由此可得到我们的第一个机器学习算法,梯度下降算法:

在我们之前讲到梯度下降的时候,我们用到的是这个图:
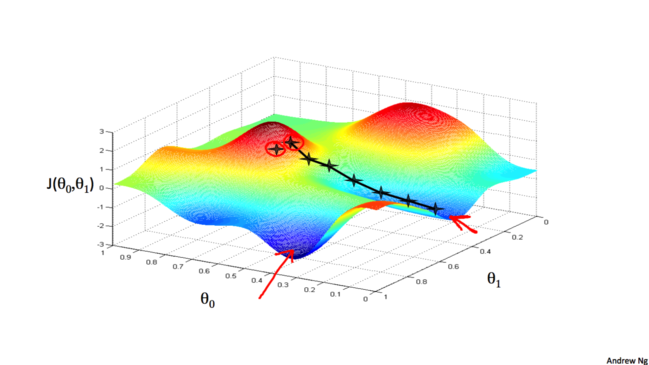
起始点不同,会得到不同的局部最优解。但事实上,用于线性回归的代价函数总是一个凸函数(Convex
Function)。这样的函数没有局部最优解,只有一个全局最优解。所以我们在使用梯度下降的时候,总会得到一个全局最优解。
下面我们来看一下梯度下降的运行过程:

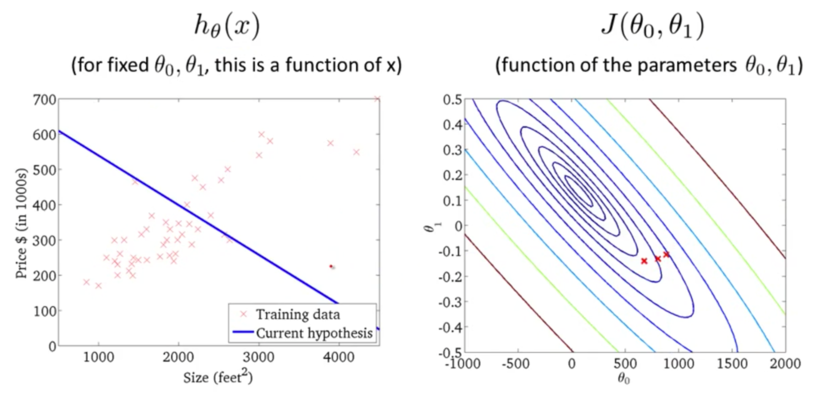
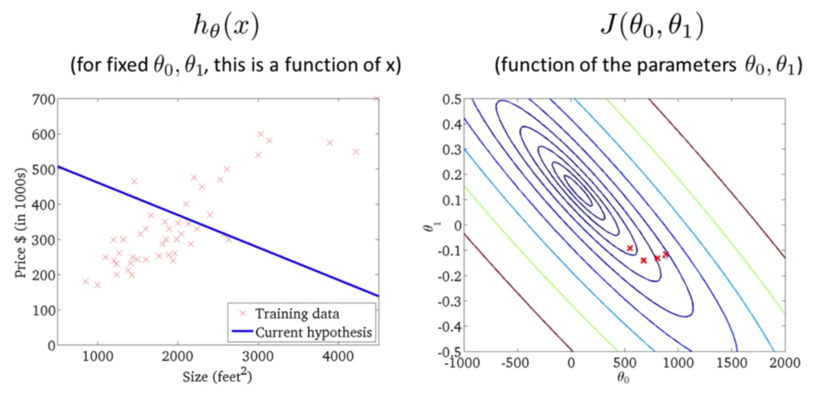
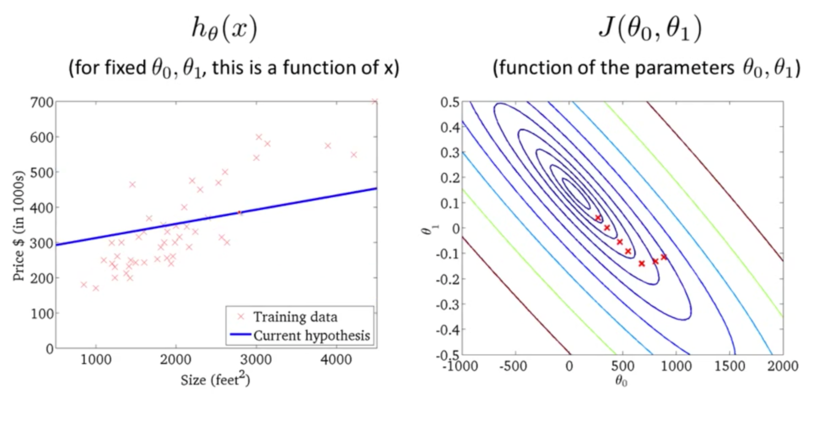
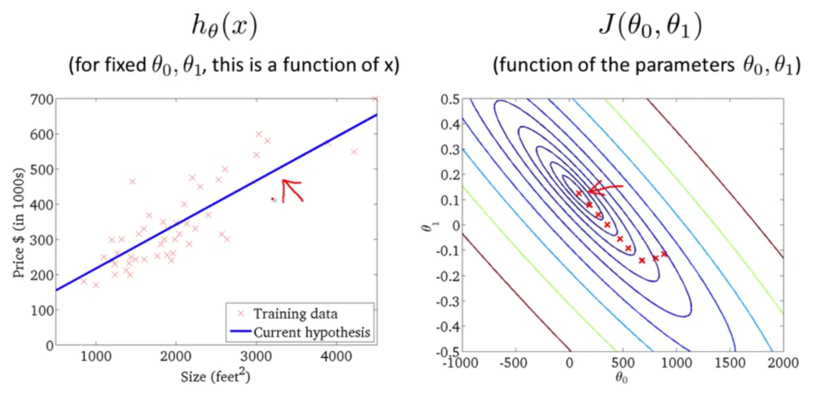
迭代多次后,我们得到了最优解。现在我们可以用最优解对应的假设函数来对房价进行预测了。例如一个1,250平方英尺的房子大概能卖到250k$,如下图所示:
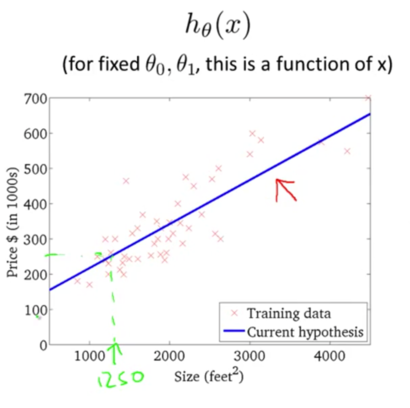
最后我们在介绍几个相关的概念。刚才我们用到的梯度下降也叫作批梯度下降(Batch Gradient
Descent)。这里的‘批’的意思是说,我们每次更新$\theta$的时候,都是用了所有的训练样例(training
example)。当然也有一些其他的梯度下降,在后面的课程中会介绍到。

在后面的课程中我们还会学习到另一种不需要像梯度下降一样多次迭代也能求出最优解的方法,那就是正规方程(Normal
Equation)。但是在数据量很大的情况下,梯度下降比较适用。
|