| 编辑推荐: |
本文主要介绍基于随即梯度下降的学习优化算法的困局用内嵌 TDA 的深度学习架构来解围,希望对您的学习有所帮助。
本文来自于知乎,由火龙果软件Alice编辑、推荐。 |
|
引言
基于随机梯度下降(SGD)的优化算法的困局:
之前在学校的时候,我曾试图利用内网的论坛给学生洗脑,批判当下深度学习的几个瓶颈和未来 TDA 可以带来的贡献和突破。说实在,现在看来,那时是
too young too simple 了:深度学习的梅开二度是有坚实的使用场景和卓越的效果来支撑的。在自己也玩了一阵子一些开源的深度学习框架后,回顾当初的论断(训练的封闭性,数据/信号的单向流动-非双向互动的学习,以及学习流程相对的静态和局部性),虽然仍然难以推翻,但是当下研究的火热的强化学习,主动/线上学习和迁移学习(transfer/generative
learning)的发展方向,都在试图突破这些深度学习先天的局限。尽管如此,一些目前深度学习赖以安身立命的关键算法技巧,其满足的条件和应用的场景都如此的苛刻,似乎除了图像和语音方面的应用,仿佛一位柔弱的美女前台,除了给进门的客人带来初次一见的惊艳,此外让人都不好意思要求她还能做些什么别的。
是的,我说的其中一个问题就是基于随即梯度下降(Stochastic Gradient Descent)的学习优化算法。简单来讲,SGD
起到的关键作用在于为一个深度学习模型在封闭的训练过程中,指出迭代优化的方向。在很多图像和语音的数据上,配上强大的运算硬件,SGD
有着让人吃惊的效果,让模型很有效的往最小化学习误差(learning loss)的方向训练/学习,将最后的测试效果显著提升,例如一炮而红的
AlexNet 和 AlphaGo。但是在许多充满噪音和随机性的训练数据上,基于 SGD 的优化器会陷于局部的最优解的大坑里很难爬出来,如下图陷入的星号标记的洼地(这还不提它所需要的误差函数的可微分性):
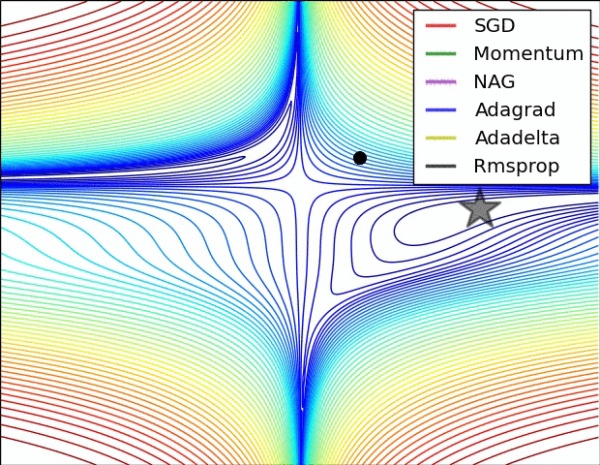
更骇人的漏洞在于,这些基于 SGD 的优化算法,很容易被人利用,做一些让人类看起来不可思议的蠢事,即所谓的
对抗样本(adversarial examples):
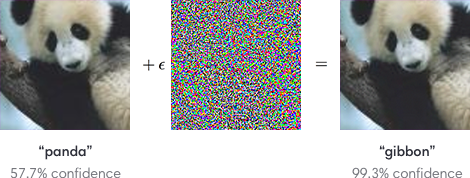
这里同样肉眼看来都是熊猫的图,加了马赛克的右边的图在机器看来就是猿猴。
这样的漏洞,在深度学习实际的应用中有可能是致命的。例如,自动驾驶依赖对于路标的图像识别,如果像上面那样,给前行的路标贴一层肉眼看不出来的马赛克,让机器读起来有很高的概率认为是向左转,嘿嘿。。。所以下次您在十字路口看到对面开过来一台特斯拉,小心点开慢点是没错的。
除此之外,同样来自 OpenAI 的 Chris Olah 的博客 Colah 有一篇很开脑洞的博文。这篇以神经网络,流形和拓扑学
命名的博文也指出当前深度学习在完全忽略训练数据的全貌和形状下在模型初始化(initialisation)和参数维度(dimensionality)设定上有可能吃的亏,以及拓扑学可以带来的解救。
接下来,我们来说说 TDA 能提供的解药。
来自 TDA 的解救
这个时候,TDA 或者拓扑学中深厚的积淀或许能挑出一些现成的工具来解围。
其一,是拓扑学识别局部最优解和全局最优解的能力(local minimum vs. global
minimum):
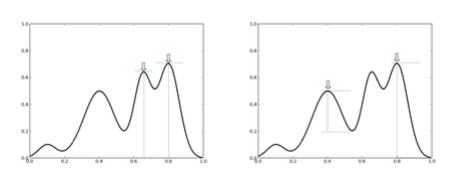
这里,犹他州立的王贝 教授 在训练主动学习模型时,代入 TDA 具备的识别「更全局」的最优解的能力
去做主动寻找(筛选)模型训练的子样本,如上图的左图的训练数据是根据局部解去筛选训练样本,而基于TDA的筛选的最优解是更全局的两个峰值。
其二,是拓扑学其中的一个理论(Morse Smale Theory),当中对于局部最优解的配对和对消的可能性的定论(critical
point offsetting)可以让误差函数的优化变得更加直接和有效:
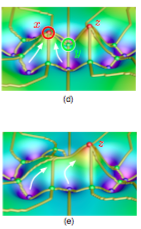
这里的上图中有3个极值:x,y 和 z。其中 x 和 y 是相对于 z 的局部极值,Morse Smale
理论告诉我们,在不改变标的空间的(同调)拓扑结构的前提下,通过简单的微调,可以对消 x 和 y,剩下
z 作为名副其实的全局极值(global critical point)作为优化的目标点。
其三,是在之前的专栏文章中展开论述的, TDA 的抗噪性和捕捉周期性的能力。
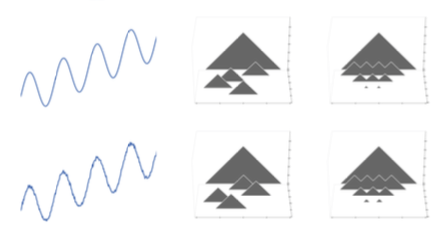
上图的左边是两个波形的数据集,区别在于下面的波形是有锯齿状的噪音的,但通过 TDA 跑出来的 持续性峰群(persistent
landscape),所获得的结果(中间和右边的图),上下图比较一下,可以看到基本上没有受到这些噪音的影响。
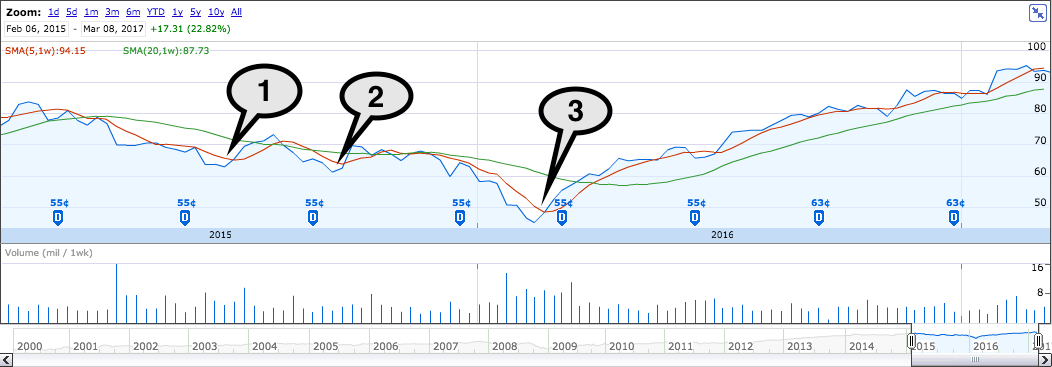
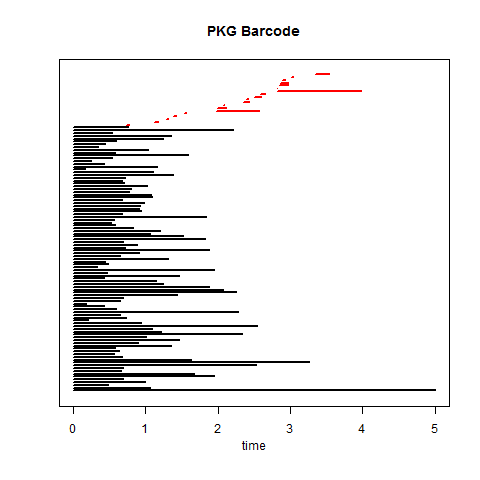
同样,之前用 TDA 分析股票价格的时序数据,如上图,通过条形码的长短(红色的线条)也能很快的识别出真正的涨跌周期,而不是当中的小幅的震荡波动。
内嵌 TDA 的深度学习架构呼之欲出
下面是 台湾中研院团队 做的一个用来给音乐音频的时序数据做标签分类的模型的 TDA + CNN 架构。三层卷积神经网络(Convolutional
Neural Network)的中间一层,加入了 TDA 计算持续性同调(persistent homology)拓扑结构的组件,然后和
CNN 并联,从而增强了模型对于高频周期性信号的捕捉能力。
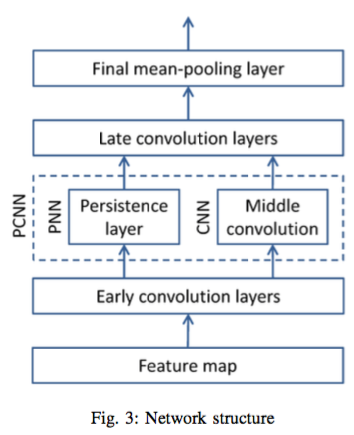
富士研究院也用类似的架构(时序数据的深度学习)来分析其它的时序数据,获得更强劲的效果:
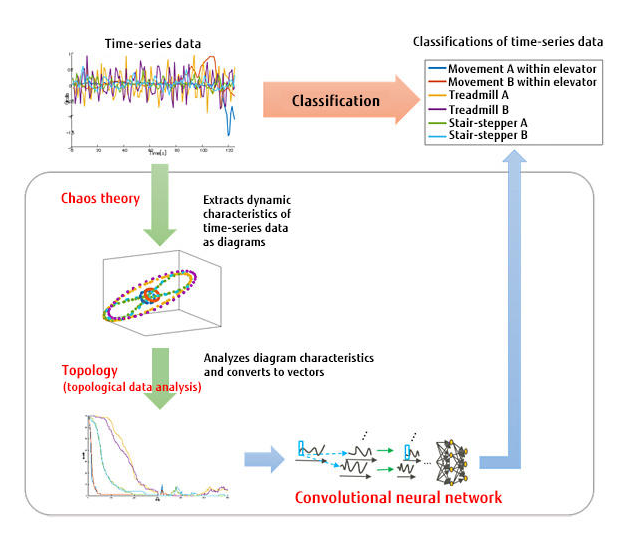
这里附上他们的 论文链接。
强在哪儿?
中研院团队的模型架构,较之过去最优的CNN音频模型,有统计上量化的准确率的提升。
背后直观感性的原因,我想是:TDA 提取出来的信号填补了传统 CNN 缺失的针对时序数据当中的周期性特征的
强 捕捉能力。
而富士实验室则声称达到了 接近 25% 的精准度的提升。
总结来说,TDA 在深度学习当中可以贡献的价值在于它在深度学习比较难学到的(周期性)特征的提取上
和学习成本的 优化的指引 上。我们有理由期待更多的这个方向的研发成果和商业应用。T.B.C。
|