| 编辑推荐: |
文章介绍了如何建立起一个任意层数的深度神经网络。这个神经网络可以应用于二元分类的监督学习问题。
本文来自于百度,由火龙果软件Alice编辑、推荐。 |
|
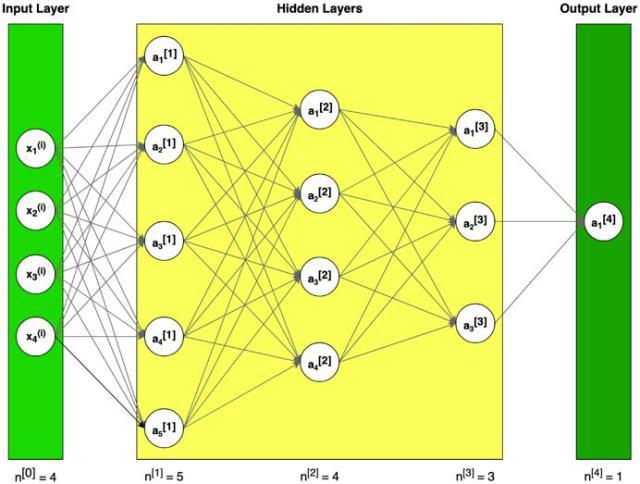
图1 神经网络构造的例子(符号说明:上标[l]表示与第l层;上标(i)表示第i个例子;下标i表示矢量第i项)
单层神经网络
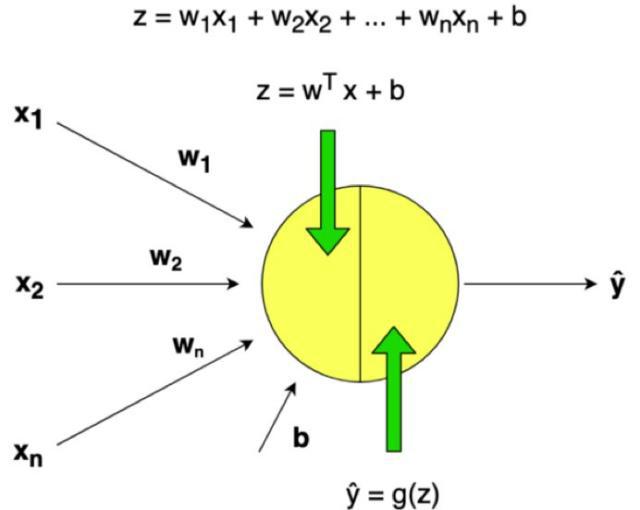
图2 单层神经网络示例
神经元模型是先计算一个线性函数(z=Wx+b),接着再计算一个激活函数。一般来说,神经元模型的输出值是a=g(Wx+b),其中g是激活函数(sigmoid,tanh,
ReLU, …)。
数据集
假设有一个很大的数据库,里面记录了很多天气数据,例如,气温、湿度、气压和降雨率。
问题陈述:
一组训练数据m_train,下雨标记为(1),不下雨标记为(0)。
一个测试数据组m_test,标记是否下雨。
每一个天气数据包含x1=气温,x2=湿度,x3=气压。
机器学习中一个常见的预处理步骤是将数据集居中并标准化,这意味着从每个示例中减去整个numpy数组的平均值,然后将每个示例除以整个numpy数组的标准偏差。

通用方法(建立部分算法)
使用深度学习来建造模型
1. 定义模型构造(例如,数据的输入特征)
2. 初始化参数并定义超参数
迭代次数
在神经网络中的L层的层数
隐藏层大小
学习率α
3. 迭代循环
正向传播(计算电流损耗)
计算成本函数
反向传播(计算电流损耗)
升级参数(使用背景参数和梯度)
4. 使用训练参数来预测标签
初始化
更深层次的L-层神经网络的初始化更为复杂,因为有更多的权重矩阵和偏置向量。下表展示了不同结构的各种层级。
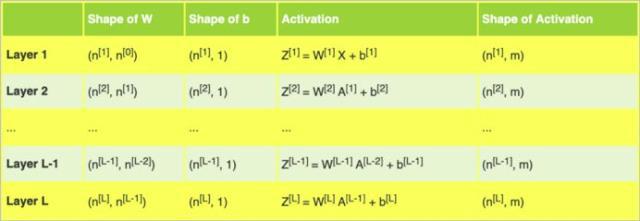
表1 L层的权重矩阵w、偏置向量b和激活函数z
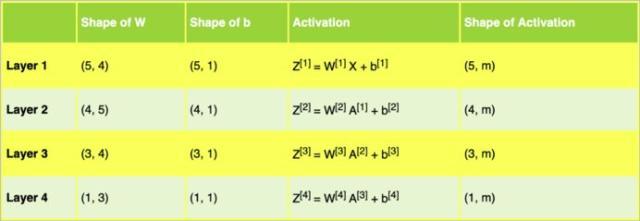
表2 示例架构中的神经网络权重矩阵w、偏置向量b和激活函数z
表2帮助我们为图1中的示例神经网络架构的矩阵准备了正确的维度。
import numpy
as np
import matplotlib.pyplot as plt
nn_architecture = [
{"layer_size": 4,"activation":
"none"}, # input layer
{"layer_size": 5,"activation":
"relu"},
{"layer_size": 4,"activation":
"relu"},
{"layer_size": 3,"activation":
"relu"},
{"layer_size": 1,"activation":
"sigmoid"}
]
def initialize_parameters(nn_architecture,
seed = 3):
np.random.seed(seed)
# python dictionary containingour parameters
"W1", "b1", ..., "WL","bL"
parameters = {}
number_of_layers = len(nn_architecture)
for l in range(1,number_of_layers):
parameters['W' + str(l)] =np.random.randn(
nn_architecture[l]["layer_size"],
nn_architecture[l-1]["layer_size"]
) * 0.01
parameters['b' + str(l)] =np.zeros((nn_architecture[l]["layer_size"],
1))
return parameters |
代码段1 参数初始化
使用小随机数初始化参数是一种简单的方法,但同时也保证算法的起始值足够好。
记住:
· 不同的初始化工具,例如Zero,Random, He or Xavier,都会导致不同的结果。
· 随机初始化能够确保不同的隐藏单元可以学习不同的东西(初始化所有权重为零会导致,所有层次的所有感知机都将学习相同的东西)。
· 不要初始化为太大的值。
激活函数
激活函数的作用是为了增加神经网络的非线性。下例将使用sigmoid and ReLU。
Sigmoid输出一个介于0和1之间的值,这使得它成为二进制分类的一个很好的选择。如果输出小于0.5,可以将其分类为0;如果输出大于0.5,可以将其分类为1。
def sigmoid(Z):
S = 1 / (1 + np.exp(-Z))
return S
def relu(Z):
R = np.maximum(0, Z)
return R
def sigmoid_backward(dA, Z):
S = sigmoid(Z)
dS = S * (1 - S)
return dA * dS
def relu_backward(dA, Z):
dZ = np.array(dA, copy = True)
dZ[Z <= 0] = 0
return dZ |
代码段2 Sigmoid和ReLU激活函数,及其衍生物
在代码段2中,可以看到激活函数及其派生的矢量化编程实现。该代码将用于进一步的计算。
正向传播
在正向传播中,在层l的正向函数中,需要知道该层中的激活函数是哪一种(sigmoid、tanh、ReLU等)。前一层的输出值为这一层的输入值,先计算z,再用选定的激活函数计算。

图3 神经网络的正向传播
线性正向模块(对所有示例进行矢量化)计算以下方程式:
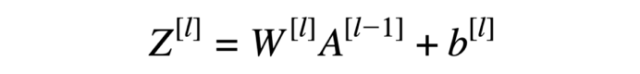
方程式1 线性正向函数
def L_model_forward(X,
parameters, nn_architecture):
forward_cache = {}
A = X
number_of_layers =len(nn_architecture)
for l in range(1,number_of_layers):
A_prev = A
W = parameters['W' + str(l)]
b = parameters['b' + str(l)]
activation =nn_architecture[l]["activation"]
Z, A =linear_activation_forward(A_prev, W,
b, activation)
forward_cache['Z' + str(l)] =Z
forward_cache['A' + str(l)] =A
AL = A
return AL, forward_cache
def linear_activation_forward(A_prev, W, b,
activation):
if activation =="sigmoid":
Z = linear_forward(A_prev, W,b)
A = sigmoid(Z)
elif activation =="relu":
Z = linear_forward(A_prev, W,b)
A = relu(Z)
return Z, A
def linear_forward(A, W, b):
Z = np.dot(W, A) + b
return Z |
代码段3 正向传播模型
使用“cache”(python字典包含为特定层所计算的a和z值)以在正向传播至相应的反向传播期间传递变量。它包含用于反向传播计算导数的有用值。
损失函数
为了管程学习过程,需要计算代价函数的值。下面的公式用于计算成本。
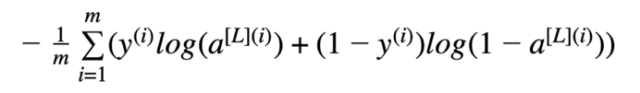
方程式2 交叉熵成本
def compute_cost(AL,
Y):
m = Y.shape[1]
# Compute loss from AL and y
logprobs =np.multiply(np.log(AL),Y) + np.multiply(1
- Y, np.log(1 - AL))
# cross-entropy cost
cost = - np.sum(logprobs) / m
cost = np.squeeze(cost)
return cost |
代码段4 代价函数的计算
反向传播
反向传播用于计算参数的损失函数梯度。该算法是由微分学中已知的“链规则”递归使用的。
反向传播计算中使用的公式:
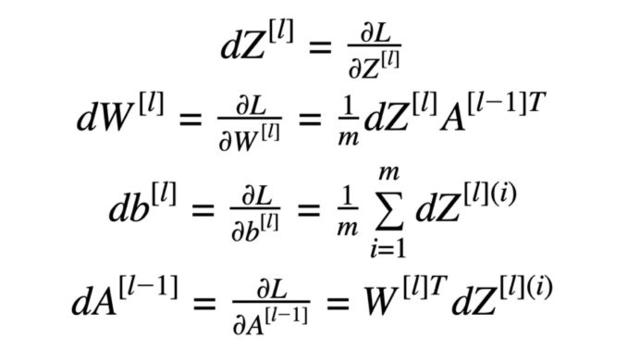
方程式3 反向传播计算公式
链式法则是计算复合函数导数的公式。复合函数就是函数套函数。

方程式4 链规则示例
“链规则”在计算损失时十分重要(以方程式5为例)。
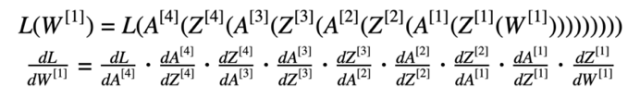
方程式5 损失函数(含替换数据)及其相对于第一权重的导数
神经网络模型反向传播的第一步是计算最后一层损失函数相对于z的导数。方程式6由两部分组成:方程式2损失函数的导数(关于激活函数)和激活函数“sigmoid”关于最后一层Z的导数。
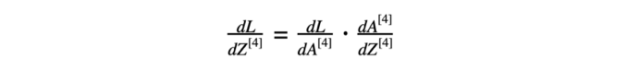
方程式6 从4层对z的损失函数导数
方程式6的结果可用于计算方程式3的导数。
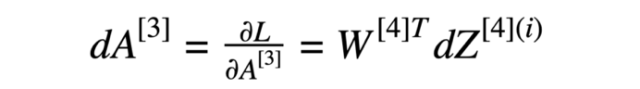
方程式7 损失函数相对于3层的导数
在进一步计算中,使用了与第三层激活函数有关的损失函数的导数(方程式7)。
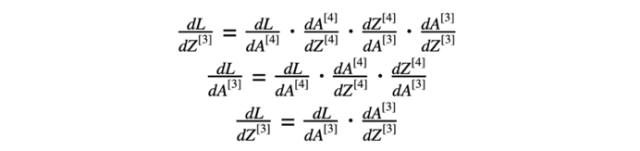
方程式8 第三层的导数
方程式7的结果和第三层活化函数“relu”的导数用于计算方程式8的导数(损失函数相对于z的导数)。然后,我们对方程式3进行了计算。
我们对方程9和10做了类似的计算。
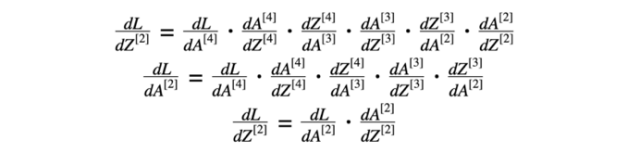
方程式9 第二层的导数
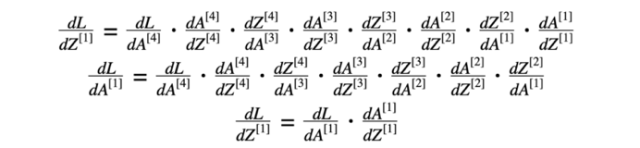
方程式10 第一层的导数
总体思路
从第一层层对z的损失函数导数有助于计算(L-1)层(上一层)对损失函数的导数。结果将用于计算激活函数的导数。

图4 神经网络的反向传播
def L_model_backward(AL,
Y, parameters, forward_cache, nn_architecture):
grads = {}
number_of_layers =len(nn_architecture)
m = AL.shape[1]
Y = Y.reshape(AL.shape) # afterthis line, Y
is the same shape as AL
# Initializing thebackpropagation
dAL = - (np.divide(Y, AL) -np.divide(1 - Y,
1 - AL))
dA_prev = dAL
for l in reversed(range(1,number_of_layers)):
dA_curr = dA_prev
activation =nn_architecture[l]["activation"]
W_curr = parameters['W' +str(l)]
Z_curr = forward_cache['Z' +str(l)]
A_prev = forward_cache['A' +str(l-1)]
dA_prev, dW_curr, db_curr =linear_activation_backward(dA_curr,
Z_curr, A_prev, W_curr, activation)
grads["dW" +str(l)] = dW_curr
grads["db" +str(l)] = db_curr
return grads
def linear_activation_backward(dA, Z, A_prev,
W, activation):
if activation =="relu":
dZ = relu_backward(dA, Z)
dA_prev, dW, db =linear_backward(dZ, A_prev,
W)
elif activation =="sigmoid":
dZ = sigmoid_backward(dA, Z)
dA_prev, dW, db =linear_backward(dZ, A_prev,
W)
return dA_prev, dW, db
def linear_backward(dZ, A_prev, W):
m = A_prev.shape[1]
dW = np.dot(dZ, A_prev.T) / m
db = np.sum(dZ, axis=1,keepdims=True) / m
dA_prev = np.dot(W.T, dZ)
return dA_prev, dW, db |
代码段5 反向传播模块
更新参数
该函数的目标是通过梯度优化来更新模型的参数。
def update_parameters(parameters,
grads, learning_rate):
L = len(parameters)
for l in range(1, L):
parameters["W" +str(l)] = parameters["W"
+ str(l)] - learning_rate *grads["dW"
+ str(l)]
parameters["b" +str(l)] = parameters["b"
+ str(l)] - learning_rate *grads["db"
+ str(l)]
return parameters |
代码段6 使用梯度下降更新参数值
全模型
神经网络模型的完整实现包括在片段中提供的方法。
def L_layer_model(X,
Y, nn_architecture, learning_rate = 0.0075,num_iterations
= 3000, print_cost=False):
np.random.seed(1)
# keep track of cost
costs = []
# Parameters initialization.
parameters =initialize_parameters(nn_architecture)
# Loop (gradient descent)
for i in range(0,num_iterations):
# Forward propagation:[LINEAR -> RELU]*(L-1)
-> LINEAR -> SIGMOID.
AL, forward_cache =L_model_forward(X, parameters,
nn_architecture)
# Compute cost.
cost = compute_cost(AL, Y)
# Backward propagation.
grads = L_model_backward(AL,Y, parameters,
forward_cache, nn_architecture)
# Update parameters.
parameters =update_parameters(parameters, grads,
learning_rate)
# Print the cost every 100training example
if print_cost and i % 100 ==0:
print("Cost afteriteration %i: %f"
%(i, cost))
costs.append(cost)
# plot the cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (pertens)')
plt.title("Learning rate=" + str(learning_rate))
plt.show()
return parameters |
代码段7 整个神经网络模型
只需要将已知的权重和系列测试数据,应用于正向传播模型,就能预测结果。
可以修改snippet1中的nn_架构,以构建具有不同层数和隐藏层大小的神经网络。此外,准备正确实现激活函数及其派生函数(代码段2)。所实现的函数可用于修改代码段3中的线性正向激活方法和代码段5中的线性反向激活方法。
进一步改进
如果训练数据集不够大,则可能面临“过度拟合”问题。这意味着所学的网络不会概括为它从未见过的新例子。可以使用正则化方法,如L2规范化(它包括适当地修改成本函数)或退出(它在每次迭代中随机关闭一些感知机)。
我们使用梯度下降来更新参数和最小化成本。你可以学习更多高级优化方法,这些方法可以加快学习速度,甚至可以为成本函数提供更好的最终价值,例如:
· 小批量梯度下降
· 动力
· Adam优化器

|