| 编辑推荐: |
本文来源于csdn,从最简单的视角分享机器学习的过程,从零开始一点一滴学习SVM算法。
|
|
SVM是最经典的分类算法之一,笔者觉得难度却是机器学习算法中最难的,对于没有数学基础的同学来说更是一头雾水。笔者作为一个初入机器学习的小白,希望能从最简单的视角分享我的学习过程,从零开始一点一滴学习SVM算法。
一、首先,什么是svm,它能够做什么?
它是一种二分类模型,解决是非的问题。
以对图像猫狗分类为例:
1.下载CIFAR数据集,数据集中有10类,我只取两类:猫、狗
2.获取猫狗混合的训练样本集,D={(x1,y1),(x2,y2),?,(xn,yn)
},yiε {?1,+1 }
3.训练样本获取分割超平面
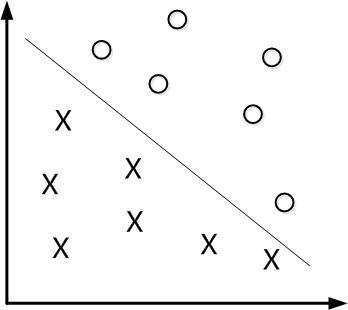
4.正确分开不同类别样本,保存模型
5.输入测试数据,进行预测
如果是应用,只想把这个算法当作工具那么以上就足够了,可以应用tensorflow、sklearn以及最近很流行,也是令我非常好奇的框架pytorch,输入相关的参数就可以进行训练
如何是对svm有强烈的好奇心,那就继续阅读笔者这个小白学习svm的过程
二、深入研究svm原理
svm最基本的想法就是基于训练集D在样本空间中找到一个划分超平面,将不同的类别样本分开,在样本空间中可以通过线性方程来描述:
wTx+b=0
样本空间中的任意点到超平面的距离为:由点到面的距离公式可知
r=|wTx+b|||w||
补充一下||w|| 的含义,对于初学者来说这种公式确实会很头疼,这个专业一点被称作L2 范式,用来衡量一个向量的长度,
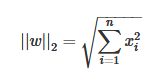
我们需要找到划分超平面对训练样本“正中间”的划分超平面,这样的超平面对样本的局部扰动的容忍性最好,也就是说我们不满足仅仅是划分开两个样本数据,我们要尽可能的使得两个分的最开。
如下图所示:
我们令 :
[Math Processing Error]
[Math Processing Error]
也就是说样本数据{[Math Processing Error]},输入到
[Math Processing Error]
如果[Math Processing Error]或者,反之[Math Processing Error]
而且在[Math Processing Error]
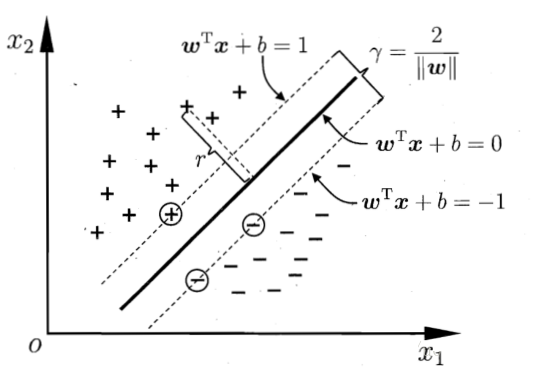
那么问题来了,为什么是[Math Processing Error]
,关键不明白那个1,设置成其他的值不行吗?答案是可以,并且可以设置成任意值,但是因为设置成1
简单,容易计算。
问题又来了,为什么可以设置成任意值,这样的话超平面还能够唯一吗?答案是可以,我们的超平面为:
[Math Processing Error]
也就是说任意的放缩w与b都不会影响超平面,因为恒为0啊
假设两条边界线为[Math Processing Error],我们两边同时除以r,得到[Math
Processing Error ]。
样本点到面的距离公式:
[Math Processing Error]
令[Math Processing Error],带入上式,这个世界回归平静了,一切都这么安详,一切好像都没有发生过。
“支持向量”到超平面的的距离即分界线到超平面的距离,根据两条线距离的公式可得:
[Math Processing Error]
它被称作为 “间隔” ,而我们的目标是,找到最大的间隔并且满足
[Math Processing Error]
[Math Processing Error]这两条约束条件即:
[Math Processing Error]
[Math Processing Error]
显然,最大化[Math Processing Error],也就是最小化[Math Processing
Error],则目标函数可以重写为:
[Math Processing Error]
[Math Processing Error]
接下来就是求解带有约束条件的目标函数,那么就要用到大名鼎鼎的拉格朗日乘子算法与KKT条件,到这不要担心,看起来很唬人(其实确实挺难的),我们简单的理解,如果目标函数的约束条件带有等式那就使用拉格朗日乘子算法,这里我引用斯坦福大学机器学习教程吴恩达老师的讲义的公式说明:如果目标函数是仅仅带有等式约束 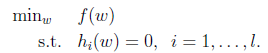
那么拉格朗日函数的形式如下: 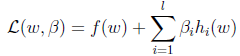
只要对w求偏导等于0,得到[Math Processing Error]的值,带入目标函数即可得到不带有约束条件的目标函数
如果带有不等式约束: 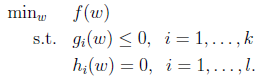
目标函数如下: 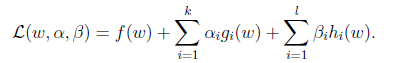
由此我们对上面的目标函数的约束进行变形
[Math Processing Error]
[Math Processing Error]
应用拉格朗日乘子算法可得:
[Math Processing Error]
对w与b求偏导为零可得
[Math Processing Error]
[Math Processing Error]
回代入公式可得目标函数变为:
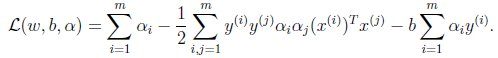
最后一项在上面的对b求偏导可知结果为0,得到的目标函数为:
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
哎,我们不是要求极小值吗?这里怎么会是极大值,对你没有看错,是极大值,因为经过拉格朗日子乘子算法得到的函数会形成一个对偶问题,啥是对偶问题?简单的理解就是求大的问题变成求小的问题,求小的问题变成大求大的问题。如果非想死磕对偶问题,斯坦福大学机器学习公开课会给你答案,因为笔者的数学基础也不是很好,对于对偶理论也没有理解的很透彻,不能”鼻子里插葱”。
总结一下我们的约束条件:
[Math Processing Error]
[Math Processing Error]
[Math Processing Error]
不要晕,感叹这些约束条件哪来的?这些约束条件都是我们上面求解过程中得到的,这些约束条件也叫KKT条件,到底什么是kkt条件这么神秘,其实就是一系列定义好的约束,要想获得极值就得满足上述条件,通过联立方程组,得到[Math
Processing Error],回带入方程组可得不带有约束的目标函数。到此我们线性分类的问题已经解决,剩下的问题是如何解决线性不可分的情况,以及如何求解目标函数,欲知后事如何请关注后面的文章核函数与SMO算法
|