|
DBSCAN(Density-Based Spatial Clustering
of Applications with Noise)聚类算法,它是一种基于高密度连通区域的、基于密度的聚类算法,能够将具有足够高密度的区域划分为簇,并在具有噪声的数据中发现任意形状的簇。我们总结一下DBSCAN聚类算法原理的基本要点:
DBSCAN算法需要选择一种距离度量,对于待聚类的数据集中,任意两个点之间的距离,反映了点之间的密度,说明了点与点是否能够聚到同一类中。由于DBSCAN算法对高维数据定义密度很困难,所以对于二维空间中的点,可以使用欧几里德距离来进行度量。
DBSCAN算法需要用户输入2个参数:一个参数是半径(Eps),表示以给定点P为中心的圆形邻域的范围;另一个参数是以点P为中心的邻域内最少点的数量(MinPts)。如果满足:以点P为中心、半径为Eps的邻域内的点的个数不少于MinPts,则称点P为核心点。
DBSCAN聚类使用到一个k-距离的概念,k-距离是指:给定数据集P={p(i);
i=0,1,…n},对于任意点P(i),计算点P(i)到集合D的子集S={p(1), p(2), …,
p(i-1), p(i+1), …, p(n)}中所有点之间的距离,距离按照从小到大的顺序排序,假设排序后的距离集合为D={d(1),
d(2), …, d(k-1), d(k), d(k+1), …,d(n)},则d(k)就被称为k-距离。也就是说,k-距离是点p(i)到所有点(除了p(i)点)之间距离第k近的距离。对待聚类集合中每个点p(i)都计算k-距离,最后得到所有点的k-距离集合E={e(1),
e(2), …, e(n)}。
根据经验计算半径Eps:根据得到的所有点的k-距离集合E,对集合E进行升序排序后得到k-距离集合E’,需要拟合一条排序后的E’集合中k-距离的变化曲线图,然后绘出曲线,通过观察,将急剧发生变化的位置所对应的k-距离的值,确定为半径Eps的值。
根据经验计算最少点的数量MinPts:确定MinPts的大小,实际上也是确定k-距离中k的值,DBSCAN算法取k=4,则MinPts=4。
另外,如果觉得经验值聚类的结果不满意,可以适当调整Eps和MinPts的值,经过多次迭代计算对比,选择最合适的参数值。可以看出,如果MinPts不变,Eps取得值过大,会导致大多数点都聚到同一个簇中,Eps过小,会导致一个簇的分裂;如果Eps不变,MinPts的值取得过大,会导致同一个簇中点被标记为离群点,MinPts过小,会导致发现大量的核心点。
我们需要知道的是,DBSCAN算法,需要输入2个参数,这两个参数的计算都来自经验知识。半径Eps的计算依赖于计算k-距离,DBSCAN取k=4,也就是设置MinPts=4,然后需要根据k-距离曲线,根据经验观察找到合适的半径Eps的值,下面的算法实现过程中,我们会详细说明。
对于算法的实现,首先我们概要地描述一下实现的过程:
解析样本数据文件
计算每个点与其他所有点之间的欧几里德距离
计算每个点的k-距离值,并对所有点的k-距离集合进行升序排序,输出的排序后的k-距离值
将所有点的k-距离值,在Excel中用散点图显示k-距离变化趋势
根据散点图确定半径Eps的值
根据给定MinPts=4,以及半径Eps的值,计算所有核心点,并建立核心点与到核心点距离小于半径Eps的点的映射
根据得到的核心点集合,以及半径Eps的值,计算能够连通的核心点,并得到离群点
将能够连通的每一组核心点,以及到核心点距离小于半径Eps的点,都放到一起,形成一个簇
选择不同的半径Eps,使用DBSCAN算法聚类得到的一组簇及其离群点,使用散点图对比聚类效果
然后,再详细描述聚类过程的具体实现。
计算欧几里德距离
我们使用的样本数据,来自一组经纬度坐标数据,数据文件格式类似如下所示:
116.389463 39.87194
02
116.389463 39.874577
03
116.312984 39.887419
04
116.382798 39.853576
05
116.496648 39.872999
06
116.436246 39.911165
07
116.622074 40.061037
08
116.599267 40.062485
09
116.441824 39.940168
10
116.599267 40.062485
11
116.402096 39.942057
12
116.37319 39.93428
13
116.327812 39.899396
14
116.374739 39.898751
15
116.287195 39.959335
16
116.513574 39.878222
17
116.474355 39.962825
18
116.400651 40.008559
19
... ...
|
我们需要做的首先就是,解析样本数据文件,将其转换成我们需要的表示形式,我们定义了Point2D类,代码如下所示:
01
package org.shirdrn.dm.clustering.common;
02
03
public class Point2D {
04
05
protected final Double x;
06
protected final Double y;
07
08
public Point2D(Double x, Double y) {
09
super();
10
this.x = x;
11
this.y = y;
12
}
13
14
@Override
15
public int hashCode() {
16
return 31 * x.hashCode() + 31 * y.hashCode();
17
}
18
19
@Override
20
public boolean equals(Object obj) {
21
Point2D other = (Point2D) obj;
22
return this.x.doubleValue() == other.x.doubleValue() && this.y.doubleValue() == other.y.doubleValue();
23
}
24
25
public Double getX() {
26
return x;
27
}
28
29
public Double getY() {
30
return y;
31
}
32
33
@Override
34
public String toString() {
35
return "(" + x + ", " + y + ")";
36
}
37
38
}
|
我们可以将解析后的点的对象放到一个List<Point2D> allPoints集合里面,以便后续使用时迭代集合。在计算两点之间的欧几里德距离时,需要迭代前面生成的Point2D的集合,计算欧几里德距离,实现方法如下所示:
public static double euclideanDistance(Point2D p1, Point2D p2) {
2
double sum = 0.0;
3
double diffX = p1.getX() - p2.getX();
4
double diffY = p1.getY() - p2.getY();
5
sum += diffX * diffX + diffY * diffY;
6
return Math.sqrt(sum);
7
}
|
如果需要,可以将计算的所有点之间的距离缓存,因为计算k-距离需要多次访问点的欧几里德距离,比如,可以使用Guava库中的Cache工具:
Cache<Set<Point2D>, Double> distanceCache =
CacheBuilder.newBuilder().maximumSize(Integer.MAX_VALUE).build();
|
上面代码中,设置缓存容纳足够多(Integer.MAX_VALUE)的对象,将计算出的全部的欧几里德距离放在内存中,便于后续迭代时重用。
计算k-距离
每个点都要计算k-距离,在计算一个点的k-距离的时候,首先要计算该点到其他所有点的欧几里德距离,按照距离升序排序后,选择第k小的距离作为k-距离的值,实现代码如下所示:
Task task = q.poll(); // 从队列q中取出一个Task,就是计算一个点的k-距离的任务
02
KPoint2D p1 = (KPoint2D) task.p;
03
final TreeSet<Double> sortedDistances = Sets.newTreeSet(new Comparator<Double>() { // 创建一个降序排序TreeSet
04
05
@Override
06
public int compare(Double o1, Double o2) {
07
double diff = o1 - o2;
08
if(diff > 0) {
09
return -1;
10
}
11
if(diff < 0) {
12
return 1;
13
}
14
return 0;
15
}
16
17
});
18
for (int i = 0; i < allPoints.size(); i++) { // 计算点p1与allPoints集合中每个点的k-距离
19
if(task.pos != i) { // 点p1与它自己的欧几里德距离没必要计算
20
KPoint2D p2 = (KPoint2D) allPoints.get(i);
21
Set<Point2D> set = Sets.newHashSet((Point2D) p1, (Point2D) p2);
22
Double distance = distanceCache.getIfPresent(set); // 从缓存中取出欧几里德距离(可能不存在)
23
if(distance == null) {
24
distance = MetricUtils.euclideanDistance(p1, p2);
25
distanceCache.put(set, distance); // 不存在则加入缓存中
26
}
27
if(!sortedDistances.contains(distance)) {
28
sortedDistances.add(distance);
29
}
30
if(sortedDistances.size() > k) { // TreeSet中只最多保留k个欧几里德距离值
31
Iterator<Double> iter = sortedDistances.iterator();
32
iter.next();
33
// remove (k+1)th minimum distance
34
iter.remove(); // 将k+1个距离值中最大的删除,剩余k个是最小的
35
}
36
}
37
}
38
39
// collect k-distance
40
p1.kDistance = sortedDistances.iterator().next(); // 此时,TreeSet中最大的,就是第k最小的距离
|
上述代码中,KPoint2D类是Point2D的子类,不过比基类Point2D多了一个k-距离的属性,代码如下所示:
private class KPoint2D extends Point2D {
02
03
private Double kDistance = 0.0;
04
05
public KPoint2D(Double x, Double y) {
06
super(x, y);
07
}
08
09
@Override
10
public int hashCode() {
11
return super.hashCode();
12
}
13
14
@Override
15
public boolean equals(Object obj) {
16
return super.equals(obj);
17
}
18
19
}
|
代码比较容易,可以查看相关注释信息。
绘制k-距离曲线,寻找半径Eps
x轴坐标点我们直接使用递增的自然数序列,每个点对应一个自然数,y轴就是所有点的k-距离的大小,我们在代码中可以进行处理,实现如下:
for(int i=0; i<allPoints.size(); i++) {
2
KPoint2D kp = (KPoint2D) allPoints.get(i);
3
System.out.println(i + "\t" + kp.kDistance);
4
}
|
最终生成的数据,输出格式类似如下:
0 6.795895820371257E-4
02
1 8.305064719800753E-4
03
2 8.692537028985709E-4
04
3 8.81717074805001E-4
05
4 9.38043175973106E-4
06
5 0.0010181414440047032
07
6 0.0011109837982601679
08
7 0.0011109837982601679
09
8 0.0011414013316968501
10
9 0.0011533646431092647
11
10 0.0011540277293025107
12
11 0.0011712783614491256
13
12 0.001171973122556046
14
13 0.001171973122556046
15
14 0.0012320292204251713
16
15 0.0012371273176228466
|
我们把输出数据复制到Excel表格中,使用上述数据生成散点图,基于x坐标取了4个不同的范围,观察曲线的变化情况,0~2600、0~2000、2001~2630、0~2500各个x坐标范围内的点,对应的散点图分别如下所示:
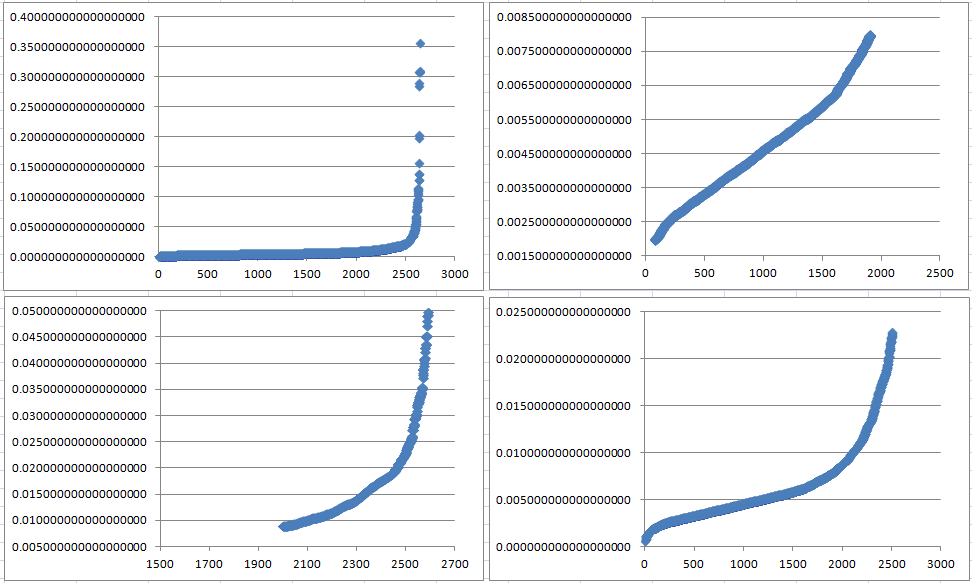
通过上图可以看出:
左上图(0~2600):由于x=2500之后店的k-距离变化太快(可以忽略),导致前面点的k-距离的变化趋势无法观察出来。
右上图(0~2000):去掉尾部的一些点的k-距离,可以看出曲线的变化趋势。
左下图(2001~2630):x坐标轴后半部分的距离的变化趋势。
右下图(0~2500):去掉尾部一些k-距离点,展示大部分k-距离点的变化趋势。
综合上面4个图,可以选择得到半径Eps的范围大致在0.002~0.006之间,已知MinPts=4,具体我们可以选择下面3个k-距离的值作为半径Eps:
0.0025094814205335555
2
0.004417483559674606
3
0.006147849217403014
|
通过下一步进行聚类,看一下使用选择的Eps的这几个值进行聚类的效果对比。另外,对半径Eps=8也进行聚类,主要是为了看一下半径变化对聚类效果的影响。
计算核心点
聚类过程需要知道半径Eps,半径已知,首先需要计算有哪些核心点,给定点,如果以该点为中心半径为Eps的邻域内的其他点的数量大于等于MinPts,则该点就为核心点。计算核心点的实现代码如下所示:
Point2D p1 = taskQueue.poll();
02
if(p1 != null) {
03
++processedPoints;
04
Set<Point2D> set = Sets.newHashSet();
05
Iterator<Point2D> iter = epsEstimator.allPointIterator();
06
while(iter.hasNext()) {
07
Point2D p2 = iter.next();
08
if(!p2.equals(p1)) {
09
double distance = epsEstimator.getDistance(Sets.newHashSet(p1, p2));
10
// collect a point belonging to the point p1
11
if(distance <= eps) { // 收集每个点与其邻域内的点之间距离小于等于Eps的点
12
set.add(p2);
13
}
14
}
15
}
16
// decide whether p1 is core point
17
if(set.size() >= minPts) { // 计算收集到的邻域内的点的个数,
小于等于MinPts,则加入到映射表Map<Point2D, Set<Point2D>> corePointWithNeighbours中
18
corePointWithNeighbours.put(p1, set);
19
LOG.debug("Decide core point: point" + p1 + ", set=" + set);
20
} else {
21
// here, perhaps a point was wrongly put outliers set
22
// afterwards we should remedy outliers set
23
if(!outliers.contains(p1)) { // 这里,会把一些点错误地加入到离群点集合outliers中,后面会进行修正
24
outliers.add(p1);
25
}
26
}
27
}
|
那些被错误放入离群点集合的点,需要在计算核心点完成之后,遍历离群点集合,与核心点集合(及其对应的映射点集合)进行比对,代码如下所示:
// process outliers
02
Iterator<Point2D> iter = outliers.iterator();
03
while(iter.hasNext()) {
04
Point2D np = iter.next();
05
if(corePointWithNeighbours.containsKey(np)) {
06
iter.remove();
07
} else {
08
for(Set<Point2D> set : corePointWithNeighbours.values()) {
09
if(set.contains(np)) {
10
iter.remove();
11
break;
12
}
13
}
14
}
15
}
|
这样,有些非离群点就从离群点集合中被排除了。
连通核心点生成簇
核心点能够连通(有些书籍中称为:“密度可达”),它们构成的以Eps长度为半径的圆形邻域相互连接或重叠,这些连通的核心点及其所处的邻域内的全部点构成一个簇。假设MinPts=4,则连通的核心点示例,如下图所示:
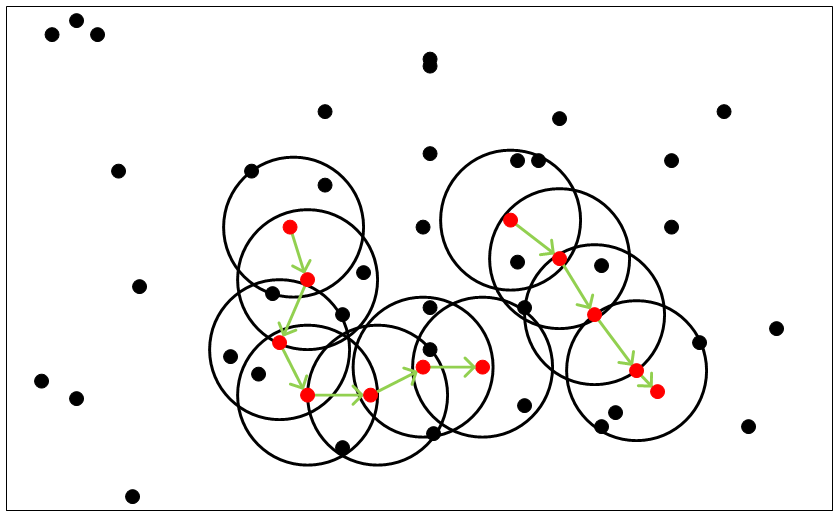
假设MinPts=4,上图中存在两个簇,每个簇都是通过核心点连通在一起的,每个簇是由连通的核心点及其核心点半径Eps圆形邻域内的点组成的,在这两个簇所覆盖的范围外部的点,都是离群点(Outliers)。
计算连通的核心点的思路是,基于广度遍历与深度遍历集合的方式:从核心点集合S中取出一个点p,计算点p与S集合中每个点(除了p点)是否连通,可能会得到一个连通核心点的集合C1,然后从集合S中删除点p和C1集合中的点,得到核心点集合S1;再从S1中取出一个点p1,计算p1与核心点集合S1集中每个点(除了p1点)是否连通,可能得到一个连通核心点集合C2,再从集合S1中删除点p1和C2集合中所有点,得到核心点集合S2,……最后得到p、p1、p2、……,以及C1、C2、……就构成一个簇的核心点。最终将核心点集合S中的点都遍历完成,得到所有的簇。具体代码实现,如下所示:
// join connected core points
02
LOG.info("Joining connected points ...");
03
Set<Point2D> corePoints = Sets.newHashSet(corePointWithNeighbours.keySet());
04
while(true) {
05
Set<Point2D> set = Sets.newHashSet();
06
Iterator<Point2D> iter = corePoints.iterator();
07
if(iter.hasNext()) {
08
Point2D p = iter.next();
09
iter.remove();
10
Set<Point2D> connectedPoints = joinConnectedCorePoints(p, corePoints);
11
set.addAll(connectedPoints);
12
while(!connectedPoints.isEmpty()) {
13
connectedPoints = joinConnectedCorePoints(connectedPoints, corePoints);
14
set.addAll(connectedPoints);
15
}
16
clusteredPoints.put(p, set);
17
} else {
18
break;
19
}
20
}
|
上面调用了重载的两个方法joinConnectedCorePoints,分别根据参数不同计算连通的核心点集合:计算核心点集合中一个点,与该核心点集合中其它的所有核心点是否连通,调用如下方法:
private Set<Point2D> joinConnectedCorePoints(Point2D p1, Set<Point2D> leftCorePoints) {
02
Set<Point2D> set = Sets.newHashSet();
03
for(Point2D p2 : leftCorePoints) {
04
double distance = epsEstimator.getDistance(Sets.newHashSet(p1, p2));
05
if(distance <= eps) {
06
// join 2 core points to the same cluster
07
set.add(p2);
08
}
09
}
10
// remove connected points
11
leftCorePoints.removeAll(set); // 删除已经确定为与p1连通的核心点
12
return set;
13
}
|
还有一个方法是,上面第一个参数变为一个集合,它调用上面的方法处理每一个点,方法代码实现如下所示:
private Set<Point2D> joinConnectedCorePoints(Set<Point2D> connectedPoints, Set<Point2D> leftCorePoints) {
2
Set<Point2D> set = Sets.newHashSet();
3
for(Point2D p1 : connectedPoints) {
4
set.addAll(joinConnectedCorePoints(p1, leftCorePoints));
5
}
6
return set;
7
}
|
最后,集合clusteredPoints存储的就是聚类后的核心点的信息,再根据核心点到其邻域内半径小于等于Eps的点的集合的映射,就能将所有的点生成聚类了。
聚类效果比较
选择不同的半径Eps进行聚类分析, 聚类的结果也不相同,有些情况下差异很大,有些情况差异较小。比如,在MinPts=4的情况下,如何绘制k-距离曲线,已经在前面详细说明了处理过程,我们根据k-距离趋势增长曲线,选择了一组半径Eps的值,执行DBSCAN聚类算法,下面我们比较在MinPts=4和MinPts=8的情况下,再分别选择不同的半径Eps,执行DBSCAN聚类算法生成簇,对分布情况进行对比。
参数:MinPts=4
选择半径Eps的值分别为如下3个观察值:
0.0025094814205335555
2
0.004417483559674606
3
0.006147849217403014
|
最终得到的聚类效果图在下面可以看到,其中,左侧为没有离群点的情况各个簇的分布情况,右侧是将离群点全部加入到图上显示,图中图例中的9999表示离群点,其他的都是聚类生成的簇,如下图所示:
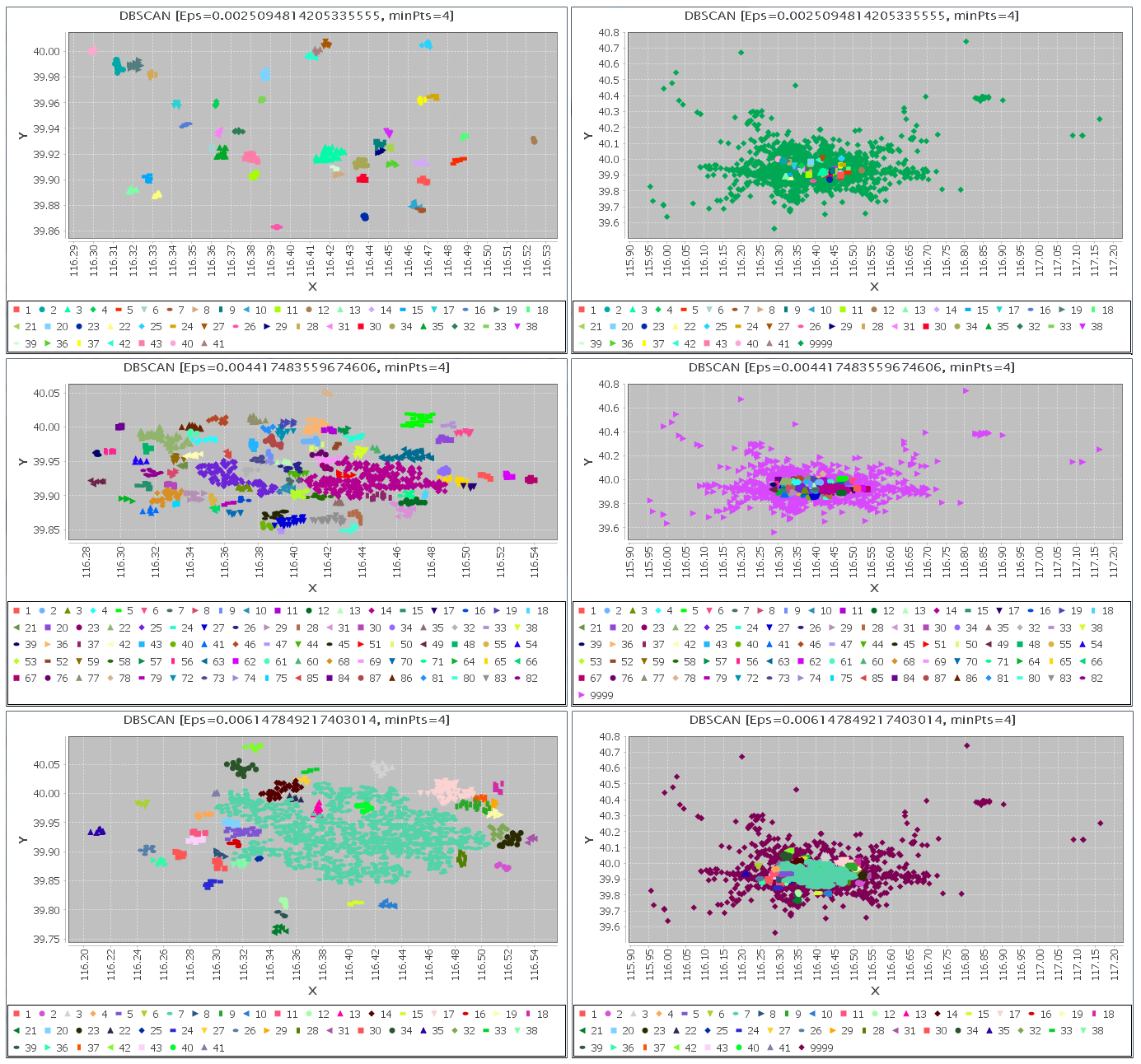
通过上图可以看出,半径Eps选择的较小时,会产生大量的离群点,其实我们想一下,半径小了,自然落在某个点的邻域内的点减少的可能性就增加了,导致很多点可能就无法成为核心点,自然也就无法成为某个簇的点,而且很生成的簇包含的点的数量都比较少,某些本来很接近的点应该可以成为同一个簇,但是被分裂了。
当半径比较大一些时,生成的一个簇包含了比较多的点,而且这个簇的形状中间可能出现一些“空洞”,因为点之间的距离大一些也能满足成为核心点的要求,所以这些点聚到一簇中可能确实比较合理。
参数:MinPts=8
选择半径Eps的值分别为如下3个观察值:
0.004900098978598581
2
0.009566439044911
3
0.013621050253196359
|
使用我们实现的DBSCAN聚类算法进行分析处理,得到的聚类结果,如下图所示:
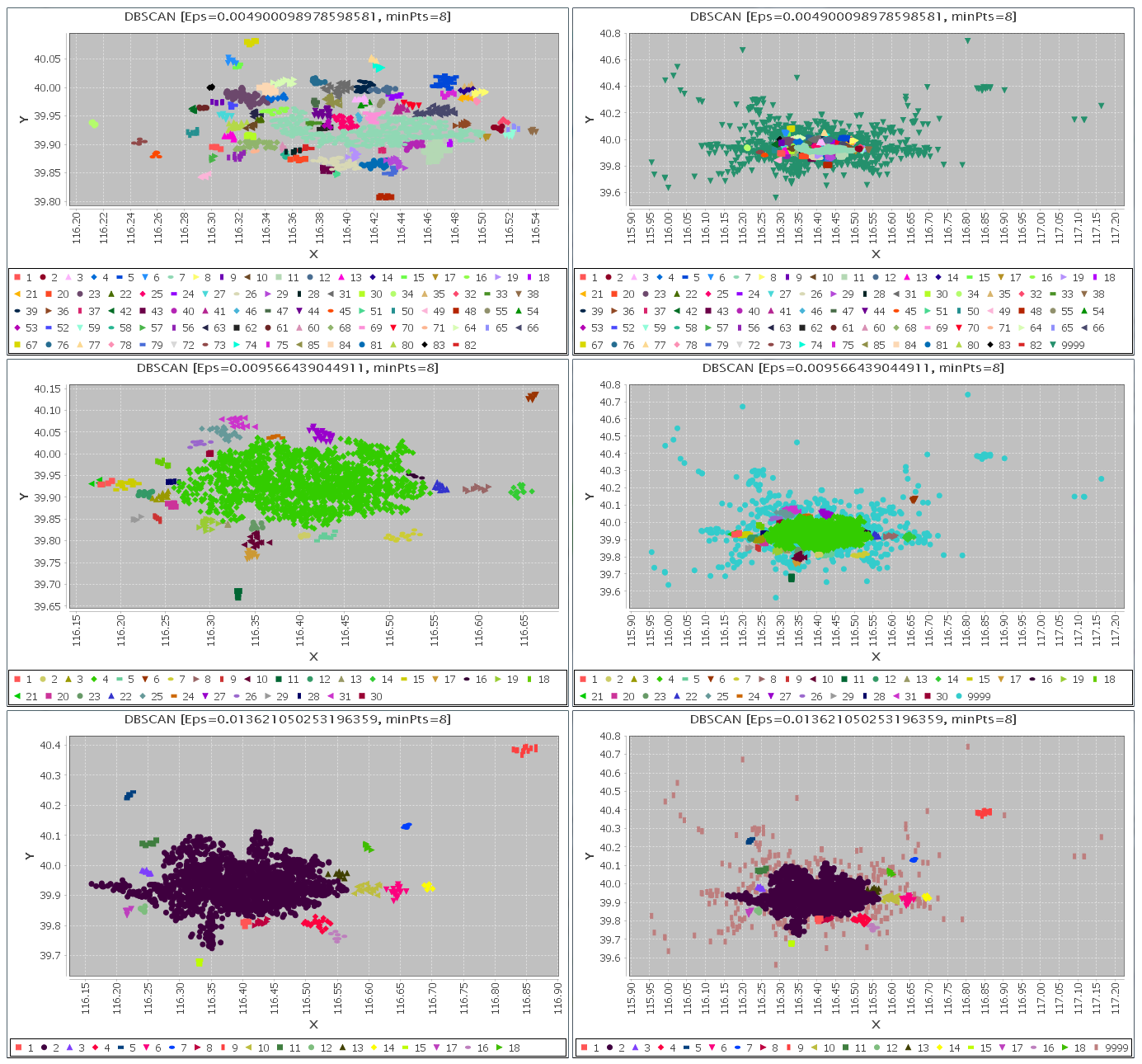
总结
因为DBSCAN聚类算法,是基于密度的聚类算法,所以对于密度分别不均,各个簇的密度变化较大时,可能会导致一些问题:比如半径Eps较大时,本来不属于同一个的簇的点被聚到一个簇中;比如半径Eps比较小时,会出现大量比较小的簇(即每个簇中含有的点不较少,但是这些点组成的小簇密度确实很大),同时出现了大量的点不满足成为核心点的要求,MinPts越大越容易出现这种情况。
DBSCAN聚类算法的思想非常明确易懂,虽然需要用户输入2个参数,但是正是输入参数的灵活性,我们可以根据自己实际应用的需要,适当调整参数值,在特定应用场景下进行聚类分析,得到合适的簇划分。通过上面选择不同参数进行聚类的结果对比,如果希望局部比较密集的点都能够生成簇,那么在固定MinPts的值的条件下,半径Eps通过调整变小,可能达到这一需要,产生的簇的数量比较多,但是同时也产生了大量分散的离群点,实际上应该可以进行二次聚类,将离群点也通过合适的方式归到指定的簇中;如果希望生成全局比较大的簇,可以适当调整半径Eps变大,生成的簇的数量较少,离群点的数量也相对较少。
|