判别分析 的SPSS操作流程

1．Discriminant Analysis判别分析主对话框 如图 1-1 所示

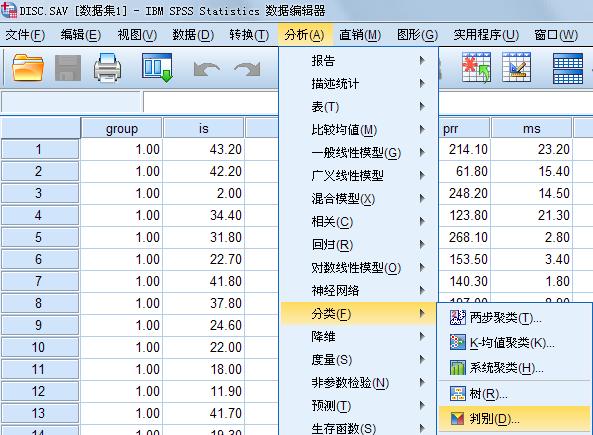
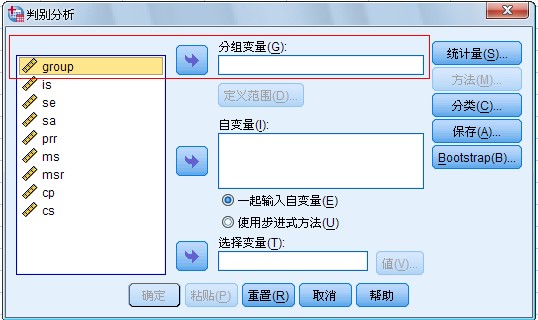
图 1-1 Discriminant Analysis 主对话框

（1）选择分类变量及其范围

在主对话框中左面的矩形框中选择表明已知的观测量所属类别的变量(一定是离散变量)， 按上面的一个向右的箭头按钮，使该变量名移到右面的Grouping Variable 框中。

此时矩形框下面的Define Range 按钮加亮，按该按钮屏幕显示一个小对话框如图1-2 所示，供指定该分类变量的数值范围。

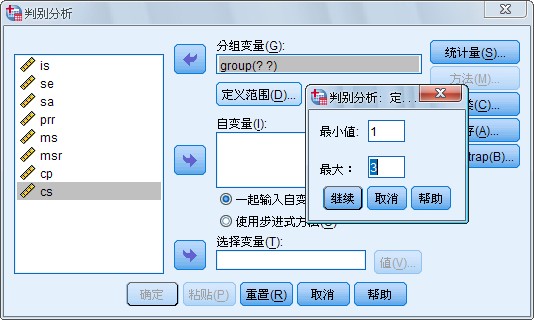
图 1-2 Define Range 对话框

在Minimum 框中输入该分类变量的最小值在Maximum 框中输入该分类变量的最大值。按Continue 按钮返回主对话框。

(2)指定判别分析的自变量

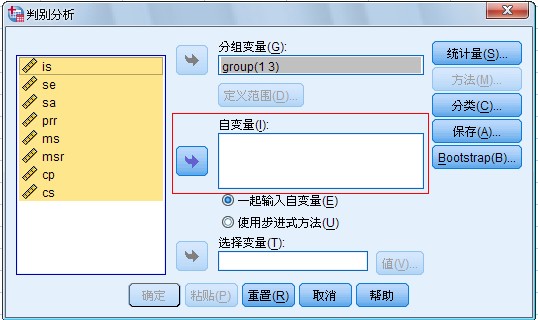
图 1-3 展开 Selection Variable 对话框的主对话框

在主对话框的左面的变量表中选择表明观测量特征的变量，按下面一个箭头按钮。

把选中的变量移到Independents 矩形框中，作为参与判别分析的变量。

（3） 选择观测量

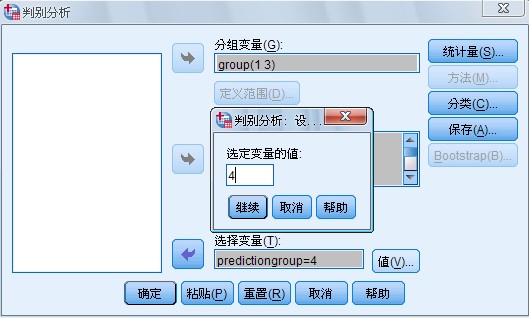
图 1-4 Set Value 子对话框

如果希望使用一部分观测量进行判别函数的推导而且有一个变量的某个值可以作为这些观测量的标识，则用Select 功能进行选择，操作方法是单击Select 按钮展开Selection Variable。选择框如图1-3 所示。

并从变量列表框中选择变量移入该框中再单击Selection Variable 选择框右侧的Value按钮，展开Set Value(子对话框)对话框，如图1-4 所示，键入标识参与分析的观测量所具有的该变量值，一般均使用数据文件中的所有合法观测量此步骤可以省略。

（4） 选择分析方法

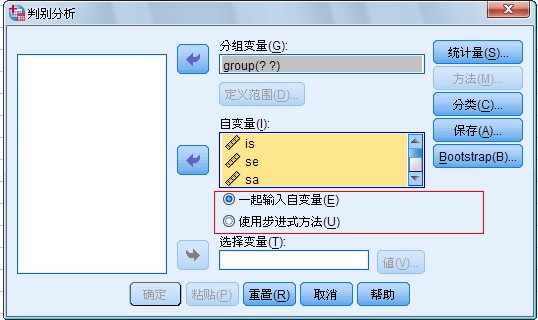
在主对话框中自变量矩形框下面有两个选择项，被选中的方法前面的圆圈中加有黑点。这两个选择项是用于选择判别分析方法的：

Enter independent together 选项，当认为所有自变量都能对观测量特性提供丰富的信息时，使用该选择项。选择该项将不加选择地使用所有自变量进行判别分析，建立全模型，不需要进一步进行选择。

Use stepwise method 选项，当不认为所有自变量都能对观测量特性提供丰富的信息时，使用该选择项。因此需要判别贡献的大小，再进行选择当鼠标单击该项时Method 按钮加亮，可以进一步选择判别分析方法。

2．Method对话框 如图 1-5 所示:　

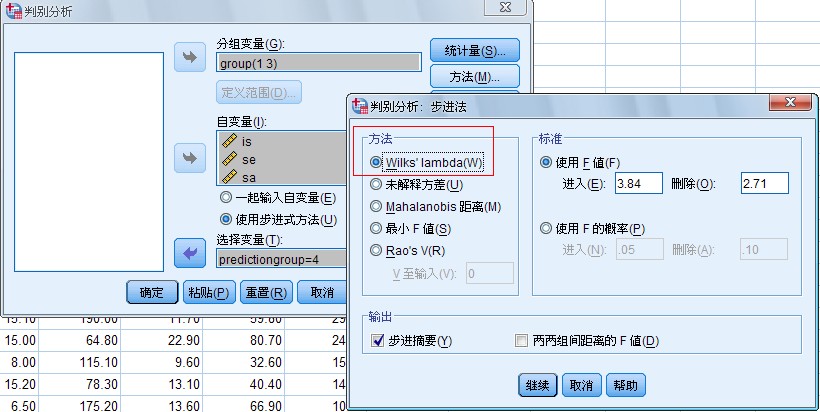
图 1-5 Stepwise Method 对话框

单击“Method”按钮展开Stepwise Method对话框。

（1）Method 栏选择进行逐步判别分析的方法

可供选择的判别分析方法有：

Wilks'lambda 选项，每步都是Wilk 的概计量最小的进入判别函数

Unexplained variance 选项，每步都是使各类不可解释的方差和最小的变量进入判别函数。

Mahalanobis’distance 选项，每步都使靠得最近的两类间的Mahalanobis 距离最大的变量进入判别函数

Smallest F ratio 选项，每步都使任何两类间的最小的F 值最大的变量进入判刑函数

Rao’s V 选项，每步都会使Rao V 统计量产生最大增量的变量进入判别函数。可以对一个要加入到模型中的变量的V 值指定一个最小增量。选择此种方法后，应该在该项下面的V-to-enter 后的矩形框中输入这个增量的指定值。当某变量导致的V值增量大于指定值的变量后进入判别函数。

(2) Criteria 栏选择逐步判别停止的判据

可供选择的判据有:

l Use F value 选项，使用F值，是系统默认的判据当加人一个变量(或剔除一个变量)后，对在判别函数中的变量进行方差分析。当计算的F值大于指定的Entry 值时，该变量保留在函数中。默认值是Entry为3.84：当该变量使计算的F值小于指定的Removal 值时，该变量从函数中剔除。默认值是Removal为2.71。即当被加入的变量F 值为3.84 时才把该变量加入到模型中，否则变量不能进入模型；或者，当要从模型中移出的变量F值<2.71时,该变量才被移出模型,否则模型中的变量不会被移出.设置这两个值时应该注意Entry值〉Removal 值。

l Use Probability of F选项，用F检验的概率决定变量是否加入函数或被剔除而不是用F值。加入变量的F值概率的默认值是0.05(5%);移出变量的F 值概率是0.10(10%)。Removal值(移出变量的F值概率) >Entry值(加入变量的F值概率)。

(3) Display栏显示选择的内容

对于逐步选择变量的过程和最后结果的显示可以通过Display 栏中的两项进行选择：

Summary of steps 复选项，要求在逐步选择变量过程中的每一步之后显示每个变量的统计量。

F for Pairwise distances 复选项，要求显示两两类之间的两两F 值矩阵。

3.Statistics对话框 指定输出的统计量如图1-6 所示：

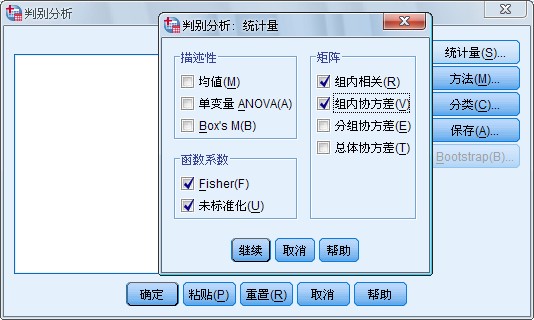
图 1-6 Statistics 对话框

可以选择的输出统计量分为以下3 类:

(l) 描述统计量

在 Descriptives 栏中选择对原始数据的描述统计量的输出：

Means 复选项，可以输出各类中各自变量的均值MEAN、标准差std Dev 和各自变量总样本的均值和标准差。

Univariate ANOV 复选项，对各类中同一自变量均值都相等的假设进行检验，输出单变量的方差分析结果。

Box’s M 复选项，对各类的协方差矩阵相等的假设进行检验。如果样本足够大，表明差异不显著的p 值表明矩阵差异不明显。

(2) Function coefficients 栏：选择判别函数系数的输出形式

Fisherh’s 复选项，可以直接用于对新样本进行判别分类的费雪系数。对每一类给出一组系数。并给出该组中判别分数最大的观测量。

Unstandardized 复选项，未经标准化处理的判别系数。

(3) Matrices 栏：选择自变量的系数矩阵

Within-groups correlation matrix复选项，即类内相关矩阵，

它是根据在计算相关矩阵之前将各组(类)协方差矩阵平均后计算类内相关矩阵。

Within-groups covariance matrix复选项，即计算并显示合并类内协方差矩阵，

是将各组(类)协方差矩阵平均后计算的。区别于总协方差阵。

Separate-groups covariance matrices复选项，对每类输出显示一个协方差矩阵。

Total covariance matrix复选项，计算并显示总样本的协方差矩阵。

4.Classification 对话框指定分类参数和判别结果 如图1-7 所示

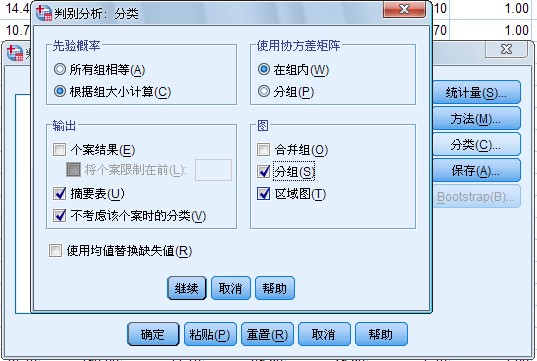
图 1-7 Classification 对话框

在主对话框中单击Classify 按钮展开相应的对话框

(1) 在 Prior Probabilities栏中选择先验概率，两者选其一

All groups equal 选项，各类先验概率相等。若分为m类，则各类先验概率均为1/m。

Compute from groups sizes选项，由各类的样本量计算决定，即各类的先验概率与其样本量成正比。

(2) Use Covariance Matrix 栏：选择分类使用的协方差矩阵

Within-groups选项，指定使用合并组内协方差矩阵进行分类。

Separate-groups选项，指定使用各组协方差矩阵进行分类。

由于分类是根据判别函数，而不是根据原始变量，因此该选择项不是总等价于二次判别。

(3) Plots 栏选择要求输出的统计图

Combined-groups复选项，生成一张包括各类的散点图。

该散点图是根据前两个判别函数值作的散点图。如果只有一个判别函数就输出直方图。

Separate-groups复选项，根据前两个判别函数值对每一类生成一张激点图，共分为几类就生成几张散点图。如果只有一个判别函数就输出直方图。

Territorial map复选项，生成用于根据函数值把观测量分到各组中去的边界图。此种统计图把一张图的平面划分出与类数相同的区域。每一类占据一个区各类的均值在各区中用*号标出。如果仅有一个判别函数，则不作此图。

(4) Display 栏选择生成到输出窗中的分类结果

Casewise results复选项，要求输出每个观测量包括判别分数、实际类、预测类(根据判别函数求得的分类结果)和后验概率等。选择此项还可以选择其附属选择项：Limits cases to复选项，并在后面的小矩形框中输入观测量数n 选择。此项则仅对前n个观测量输出分类结果。观测数量大时可以选择此项。

Summary table复选项，要求输出分类的小结，给出正确分类观测量数(原始类和根据判别函数计算的预测类相同)和错分观测量数和错分率。

Leave-one-out classification复选项，输出对每个观测量进行分类的结果，所依据的判别是由除该观测量以外的其他观测量导出的。也称为交互校验结果

(5) 在Classification对话框的最下面有一个选择项，用以选择对缺失值的处理方法。选中 Replace missing value with mean复选项，即用该变量的均值代替缺失值。该选择项前面的小矩形框中出现“.”时表示选定所示的处理方法.

5.Save对话框,指定生成并保存在数据文件中的新变量。如图1-8 所示:

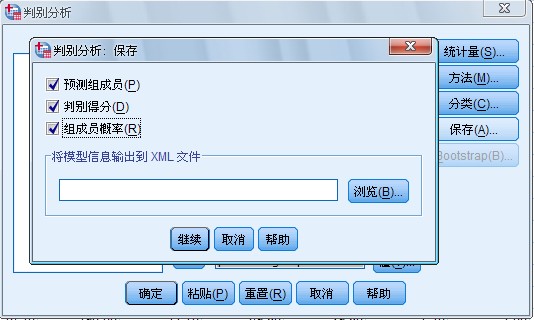
图 1-8 Save 对话框

(1) Predicted group membership复选项，要求建立一个新变量，预测观测量的分类。是根据判别分数把观测量按后验概率最大指派所属的类。每运行一次Discriminant过程，就建立一个表明使用判别函数预测各观测量属于哪一类的新变量。第1 次运行建立新变量的变量名为dis_l，如果在工作数据文件中不把前一次建立的新变量删除，第n次运行Descriminant 过程建立的新变量默认的变量名为dis_n。

(2) Discriminant score复选项，要求建立表明判别分数的新变量。该分数是由未标准化的判别系数乘自变量的值，将这些乘积求和后加上常数得来。每次运行Discriminant过程都给出一组表明判别分数的新变量，建立几个判别函数就有几个判别分数变量。参与分析的观测量共分为m类，则建立m个典则判别函数。指定该选择项，就可以生成m-l 个表明判别分数的新变量。

(3) Probabilities of group membership复选项，要求建立新变量，表明观测量属于某一类的概率。有m类，对一个观测量就会给出m个概率值，因此建立m 个新变量.

6．选择好各选择项之后，点击“OK”按钮，提交运行Discriminant过程。