|
看mysql源码的收获
- 为优化提供理论依据
- 为优化提供方向
- 学习解决问题的算法和思路
filesort algorithm
- 读取所有需要排序的数据
- 每行数据
- 算法1(original):存储排序key和行指针
- 算法2(modified):存储排序key和select中的字段
- 每次排序sort_buffer_size能容纳的行数,排序结果写入IO_CACHE对象(不妨称为IO1),本次排序结果的位置信息写入另一个IO_CACHE对象(不妨称为IO2);
- IO_CACHE超过64k时写入临时文件
- 当order by有limit n时,只需要把前n条排序结果写入IO_CACHE;
- 排序KEY长度<=20且排序KEY数量在一千和十万之间时使用radixsort,否则使用quicksort
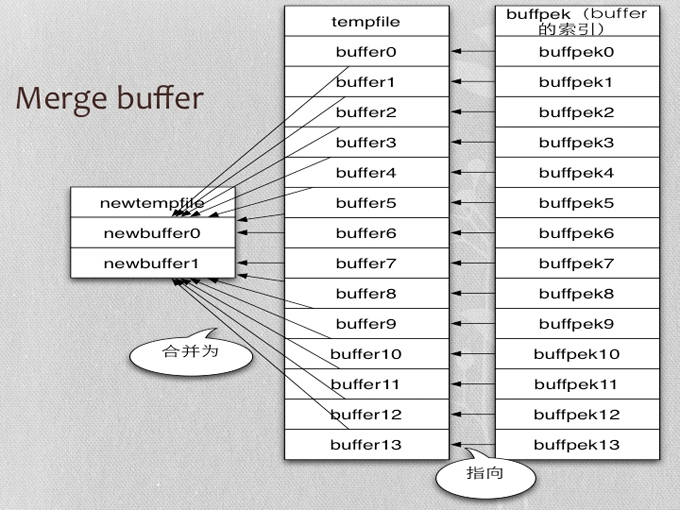
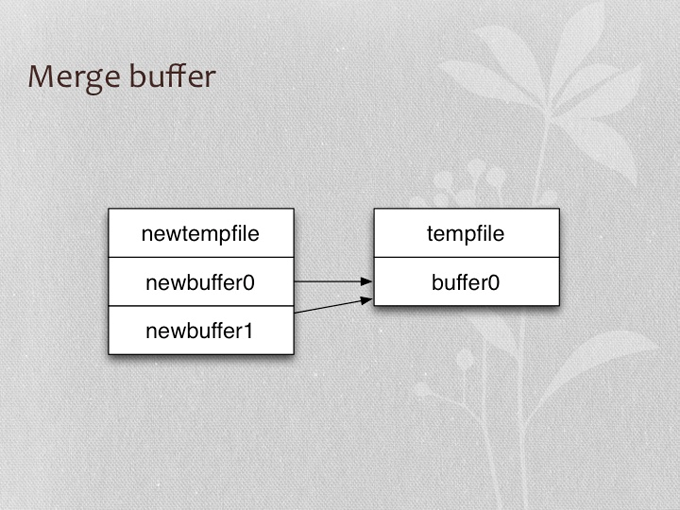
- Merge buffer
- 读取排序结果(算法2直接从临时文件读取结果;算法1从临时文件读取行指针,再从表中读取数据)
filesort algorithm选择
select bgid from bigt order by bgname;
Create Table: CREATE TABLE `bigt` (
`bgid` int(10) unsigned NOT NULL AUTO_INCREMENT,
`bgname` varchar(100) DEFAULT NULL,
`status` tinyint(4) DEFAULT ’0′,
PRIMARY KEY (`bgid`)
) ENGINE=InnoDB DEFAULT CHARSET=latin1
bgid(4字节)、bgname(102字节)、(null_fields+7)/8=1
其中null_fields是1,bgname是可以为空的字段
length=4+102+1=107
sort_length=101(bgname长度)
- 满足下两个条件之一时选择original算法
- 有text或者blob字段
- length+sortlength > max_length_for_sort_data
- 否则选择modified算法
- 本例选择了modified算法
- 没有text和blob字段
- length+sortlength=208
- max_length_for_sort_data=1024
Sort buffer内存使用
- keys= sort_buff_size/(rec_length+sizeof(char*))
- rec_length=length+sortlength
- 本例中
- rec_length=208
- sizeof(char*)=4
- sort_buff_size=2097116
- keys=9892
- 即能在内存中一次排序的key为9892个
倒序的实现
- 不是在比较KEY值大小时实现
- 发现正序、倒序,在比较KEY值大小的函数中没有区别对待
- 差点以为把整个排序过程看错了
- 是在向排序区写入KEY值时实现
- 在跟踪字符类型倒序倒序时
- make_sortkey中对每个字节取反
- 这样后续的正序排序就相当于倒序排序
正序排序Merge buffer示例
- 实际mysql源码中是每7个buffer进行合并
- 本例做了简化,只对5个buffer进行合并
- 所谓buffer是一次排序结果,保存在临时文件(IO_CACHE)中
- 5个buffer就是临时文件中的五个段,每段保存一次排序的结果
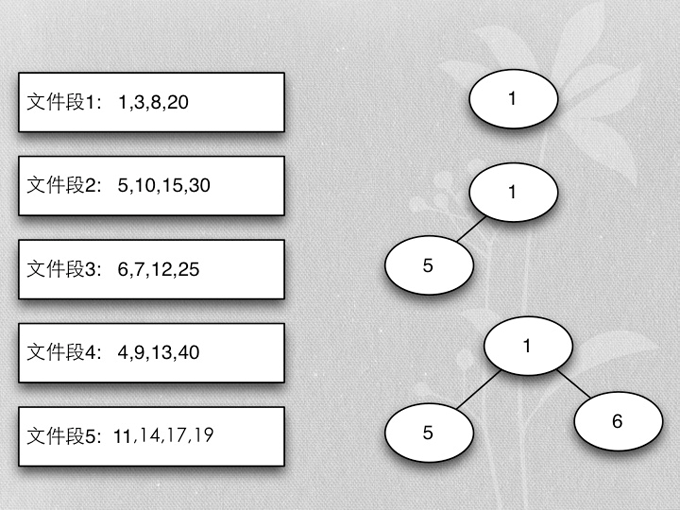
- Merge buffer的算法是heapsort实现的mergesort
- 首先每个段取第一个排序key,加入heap
- 加入时保证heap的排序
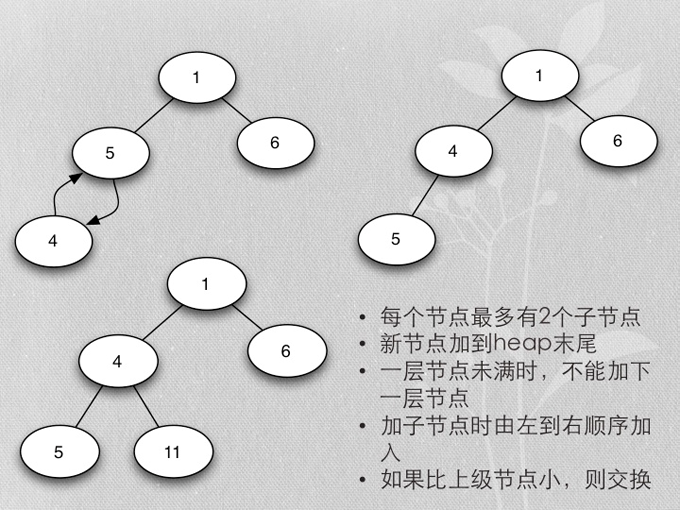
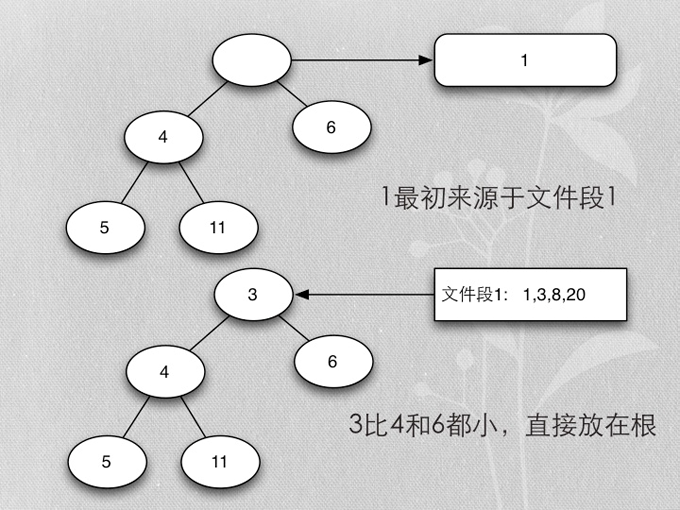
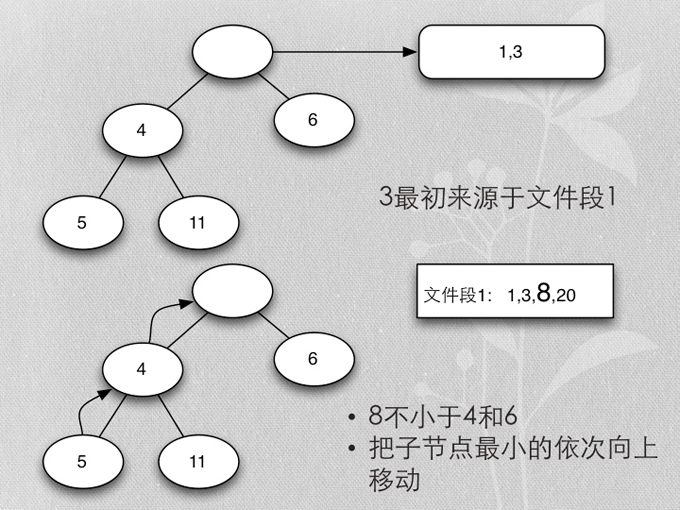
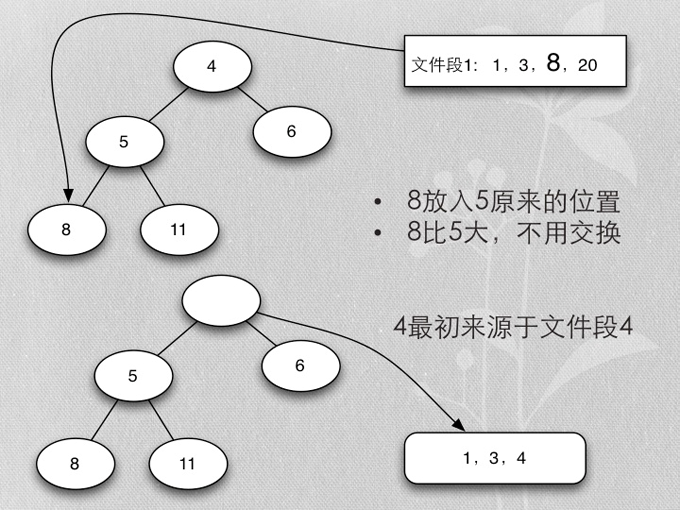
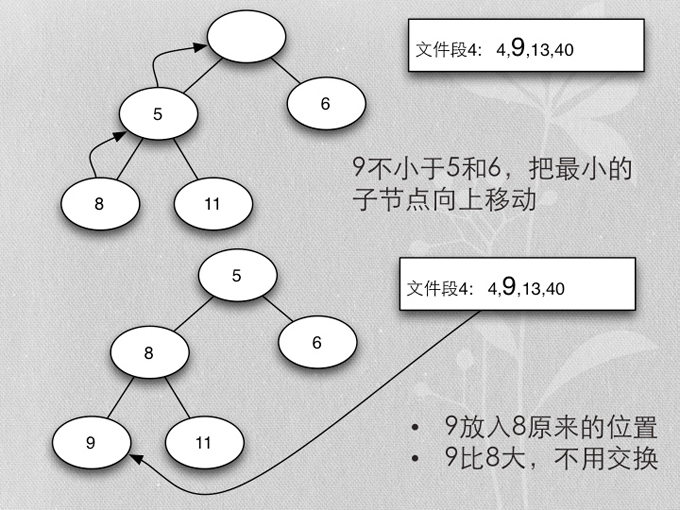
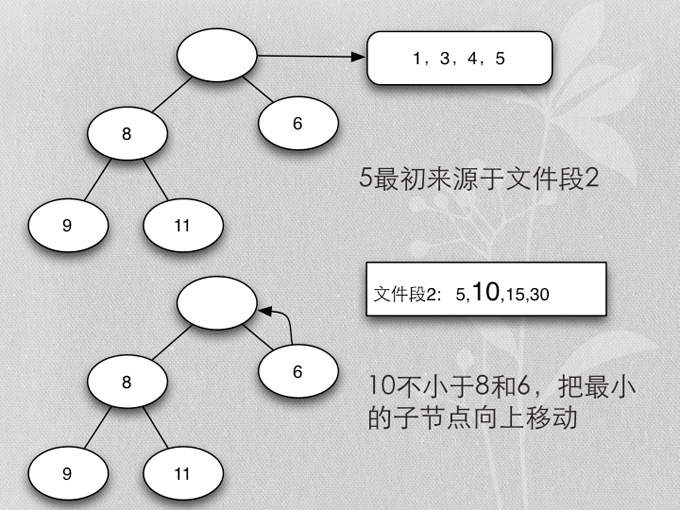
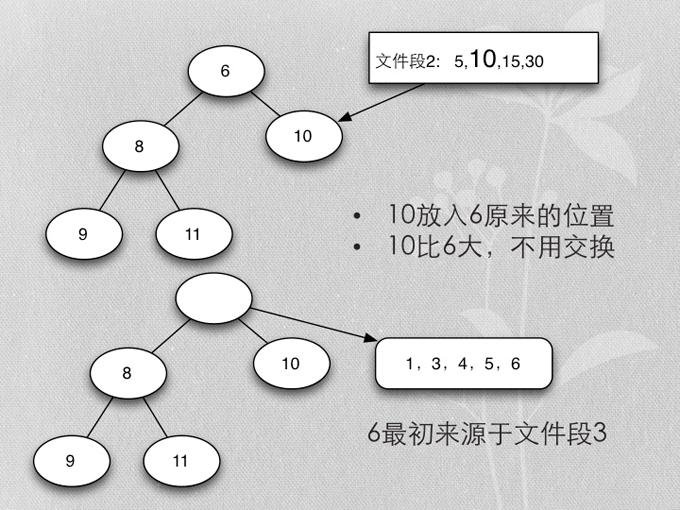
Merge buffer总结
- MySQL源码中,周而复始进行合并
- 每次合并7个buffer,直到全部合并
- 合并时仍然使用sort buffer内存
- 最后一次合并时不再向排序结果中写入排序KEY,只写需要的字段值
- 各buffer自己的最小值,在一起再取最小值,就是所有buffer数据的最小值
- 除去当前取得的最小值,再算当前buffer最小值的最小值,以此类推,得到排序的所有buffer数据
- 用heapsort实现的mergesort
为什么用heapsort?
- 每次合并若干buffer时,不能拿到所有buffer的全部数据
- 对能取到sort buffer内的所有数据完全排序是没意义的
- 以顺序排序举例,这些数据中,只有当前各buffer的最小值中的最小值能够保证是所有buffer中最小的值,依次得到这个最小值,则得到完全排序的所有数据
- heapsort也恰好是不完全排序,只保证root是最小的
运维上的思考
- 计算一个SQL是否能在内存中完成排序
- 计算一个SQL使用哪种filesort算法
- Merge buffer的代价?
- filesort旧算法与新算法资源消耗的评估?
|


