简介

在自动驾驶系统中，规划模块是实现智能行驶决策的核心环节。

Apollo自动驾驶系统通过融合高精度地图、精准定位以及对周围交通参与者的行为预测信息，综合生成安全、高效且舒适的车辆行驶轨迹。

规划过程通常分为两个关键阶段：路线规划与轨迹规划。

第一阶段是路线导航，即从全局视角确定从起点A到终点B的最优路径。这一过程以高精度地图数据为基础，结合道路拓扑结构和交通规则，输出一条宏观的可行驶路线，类似于我们日常使用的手机导航系统。在Apollo平台中，该任务由专门的路线规划模块完成。

在获得全局路线后，系统进入更精细的轨迹规划阶段。这一阶段关注局部环境下的动态决策，如避让障碍物、变道超车、路口通行等，旨在生成一条既安全又舒适的可执行轨迹。最终输出的轨迹由一系列空间点组成，每个点不仅包含位置信息，还关联有建议速度和到达时间戳，确保车辆能够平稳、准时地沿路径行驶。

可见，Apollo的规划模块通过“先全局、后局部”的分层设计，将导航指令转化为可落地的驾驶动作，为自动驾驶车辆提供从“去哪里”到“怎么去”的完整解决方案。

规划Routing

路线规划（Routing） 是规划模块的第一步，其核心目标是：在高精度地图上，为车辆找到从当前位置（A点）到目的地（B点）的最佳行驶路径。

Apollo的路线规划模块依赖三个关键输入信息：

高精度地图数据：这是路线规划的基础。Apollo地图不仅包含详细的公路网络结构（如车道、路口、交通标志等），还融合了实时交通信息（如拥堵、施工、限速变化等），为路径决策提供全面的环境支持。

车辆当前位置：通过定位模块获取的车辆在地图中的精确坐标，是路径规划的起点。

目的地（Destination）：用户设定的行车终点，是路径规划的目标。

当系统获取了以上三个输入后，路线规划模块即可启动，通过算法（如改进的Dijkstra或A*算法）在复杂的道路网络中搜索出一条最优路径。该路径通常综合考虑了距离、时间、交通状况和驾驶舒适性等因素。

最终，路线规划模块输出一条由一系列道路和车道组成的全局可行驶路径，为后续的轨迹规划（Trajectory Planning）提供宏观指导，实现从“导航到目的地”到“如何具体驾驶”的过渡。

世界转图与智能路径搜索

路线规划的核心任务之一是从地图上的起点A找到通往终点B的最优路径。人类在查看地图时通常会“沿着道路追踪”可能的路线，这一过程本质上是一种搜索（Search）。Apollo系统同样采用搜索策略，但其方法更加高效和智能化。

地图数据的图形化重构

为了实现高效搜索，Apollo在搜索开始前，会将原始的高精度地图数据重新格式化为一种称为“图”（Graph）的数据结构。这种结构是计算机科学中用于路径查找的经典模型，由两个基本元素构成：

节点（Nodes）：代表地图中的路段或关键位置，例如一条车道、一个路口区域等。

边（Edges）：代表节点之间的连接关系，即车辆可以从一个路段行驶到另一个路段的路径。例如，在一个十字路口，车辆可以从节点1分别转向节点2、3、4，这些连接关系都由边来表示。

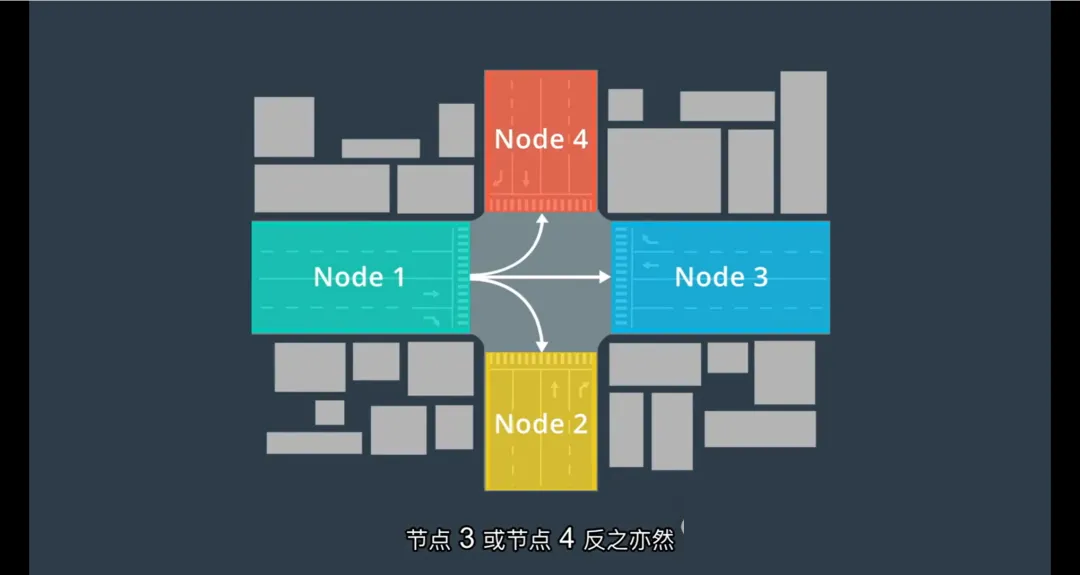
路径成本建模

在图结构中，每条边都可以被赋予一个成本（Cost），用于衡量从一个节点移动到另一个节点的“代价”。这个成本可以综合反映多种现实因素，例如：

行驶距离：距离越长，成本越高。

通行时间：考虑实时交通状况下的预计耗时。

驾驶难度：例如，转弯（尤其是左转）通常比直行更复杂、更耗时，因此转弯边的成本会高于直行边。

交通规则与信号：红灯等待、限速等也会影响成本。

通过这种方式，Apollo能够构建一个带权图（Weighted Graph），使得路径搜索不仅找到“连通”的路径，更能找到“最优”的路径。

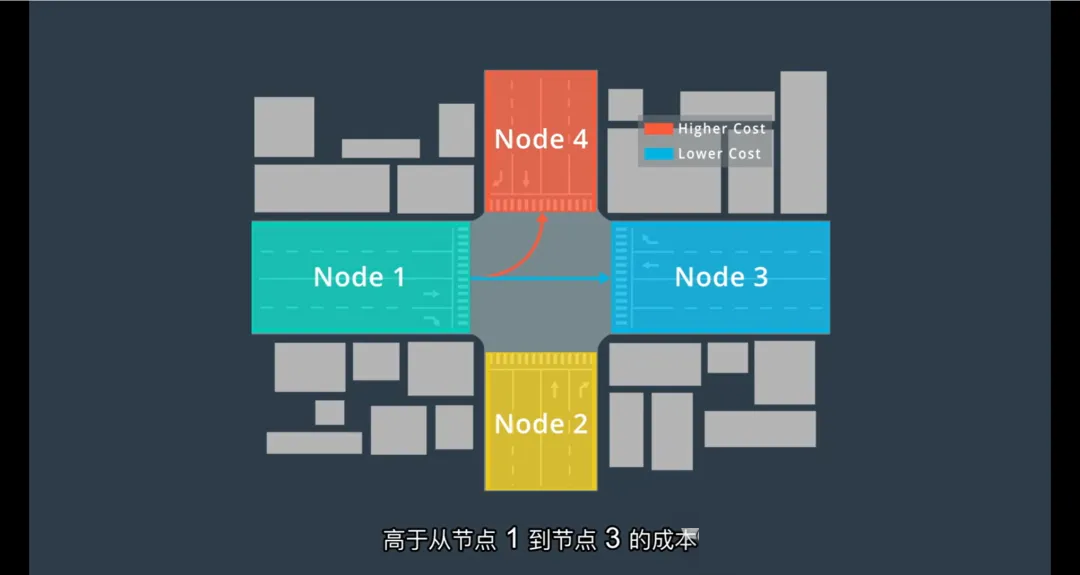
图搜索的优势

将地图转化为图结构的最大优势在于：计算机科学领域已经发展出大量高效、成熟的图搜索算法，例如：

Dijkstra算法：保证找到最短路径。

A*算法：结合启发式信息，大幅提升搜索效率，特别适合大规模地图。

Apollo利用这些算法在图中快速搜索出从起点到终点的最低成本路径。

路径的还原与应用

一旦在图结构中找到了最优路径（即一系列有序的节点和边），系统可以轻松地将这条图路径重新映射回原始的高精度地图，生成一条具体的、可行驶的路线，供后续的轨迹规划模块使用。

小结

Apollo通过将高精度地图转化为图（Graph）结构，将复杂的道路网络抽象为节点与边的连接，并引入成本模型来反映真实驾驶中的各种因素。这一设计使得系统能够利用高效的图搜索算法，快速、智能地找到从A到B的最优行驶路线，为自动驾驶的导航决策奠定了坚实基础。

网格世界

为了高效地在复杂环境中找到从起点到终点的最优行驶路线，Apollo采用了经典的A*（A-Star）路径查找算法，并将其应用于“网格世界”这一抽象模型中进行路径搜索。

什么是“网格世界”？

在Apollo的路径规划演示中，“网格世界”是一个将连续地图空间离散化的二维网格结构：

每个网格单元被视为一个节点（Node）

节点之间通过边（Edge）连接，表示可行驶的移动方向

支持最多 8个移动方向：上下左右（4方向） + 四个对角线方向

某些网格被标记为障碍物（如墙壁、禁行区），表示不可通行

这种建模方式将现实道路环境简化为一个图结构，便于计算机进行算法处理。

传统搜索的困境：指数级爆炸

如果让计算机盲目尝试所有可能路径：

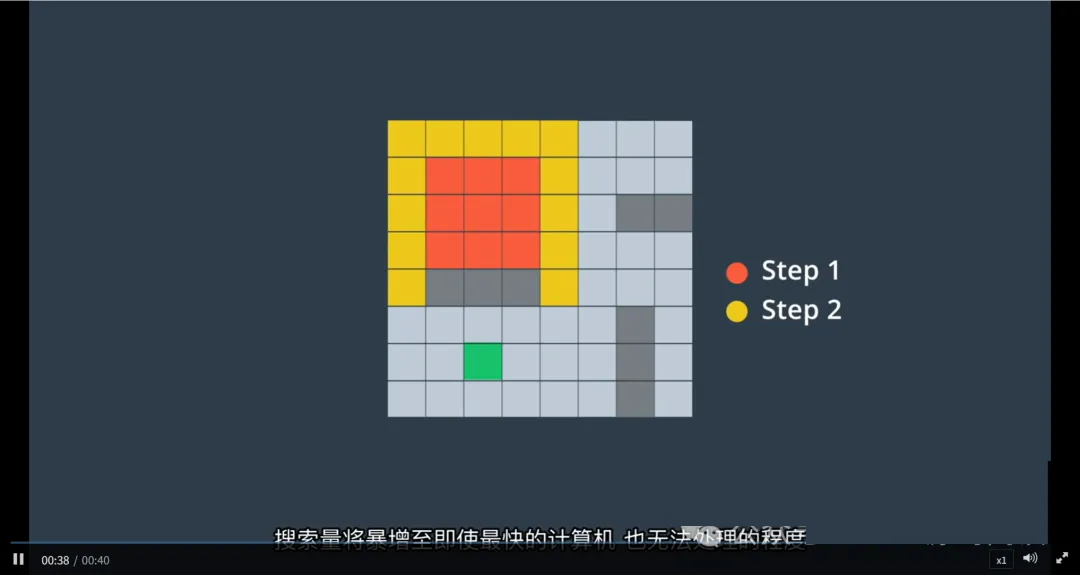
每个节点最多有8个邻居

每一步都可能产生8个新选择

随着搜索深度增加，待探索节点数量呈指数级增长

例如，在一个大型城市地图上进行全路径枚举，即使使用最快的计算机，也会因计算量过大而无法在合理时间内完成。因此，必须引入智能搜索策略。

A*算法的核心机制

A*是一种启发式搜索算法，它通过评估函数指导搜索方向，避免无效探索，显著提升效率。

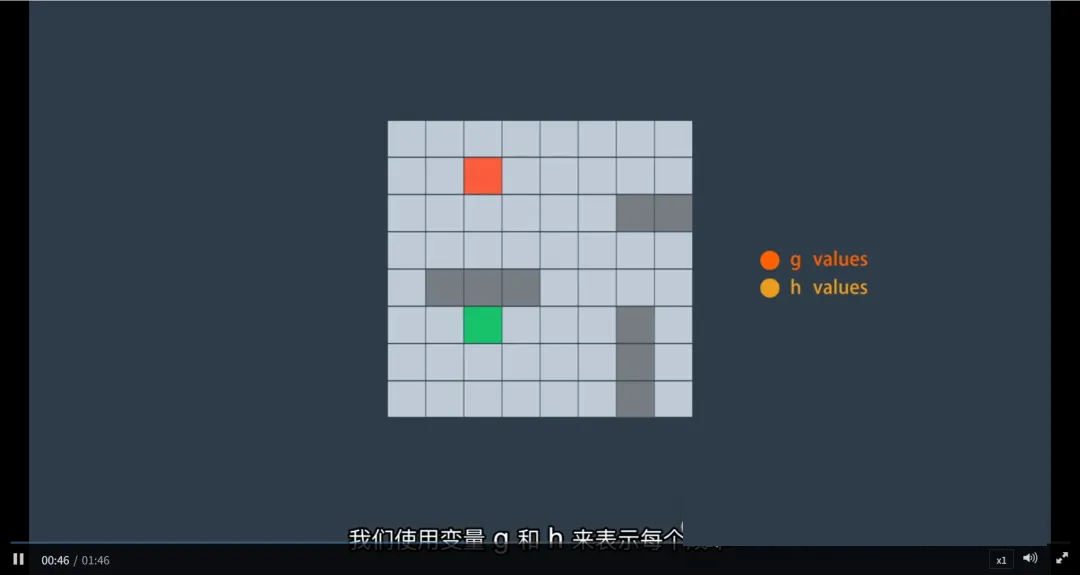
三个关键成本值

对于每一个候选节点 n ，A*计算以下三个值：

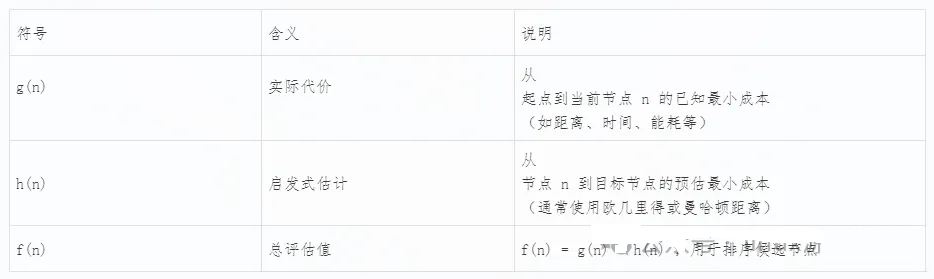
核心原则：优先扩展 f(n) 值最小的节点——即“当前成本最低 + 预计剩余成本最少”的路径。

A*的工作流程（在Apollo网格世界中）

初始化

将起点加入优先队列（按 f(n) 排序）

设置 g(起点) = 0，h(起点) = dist(起点, 目标)，计算 f(起点)

循环选择最优节点

取出 f(n) 最小且未访问过的节点作为当前节点

若当前节点是目标 → 成功，重构路径并结束

否则，将其标记为“已访问”

扩展邻居节点

遍历当前节点的8个相邻网格

跳过障碍物或越界节点

对每个合法邻居：

计算新的 g 值（考虑移动方向：直行=1，斜行=√2）

若新路径更优（g 更小），则更新其 g, h, f 值，并记录前驱节点

将其加入优先队列

重复步骤2-3

直到找到路径或队列为空（无解）

启发式函数 h(n) 的作用

h(n) 是A*的“指南针”，引导搜索朝向目标方向

在Apollo中，h(n) 不仅是几何距离，还可融合：

实时交通信息（拥堵路段 h 更高）

道路等级（高速优先）

信号灯等待时间

动态障碍物预测结果

正确设计的 h(n) 能大幅减少搜索范围，同时保证找到最优路径

Apollo中的现实扩展：超越简单网格

虽然演示中使用了简单的二维网格，但在真实Apollo系统中：

“节点”不再是网格单元，而是高精度地图中的车道段或路径点

“边”代表合法的驾驶动作（变道、转弯、直行）

成本函数 g(n) 综合考虑：

行驶时间

燃油/电耗

乘客舒适性（加速度、转向角）

安全裕度（与障碍物距离）

交通规则遵守程度

这使得A*不仅能找到“地理最短”路径，更能生成“综合最优”的驾驶策略。

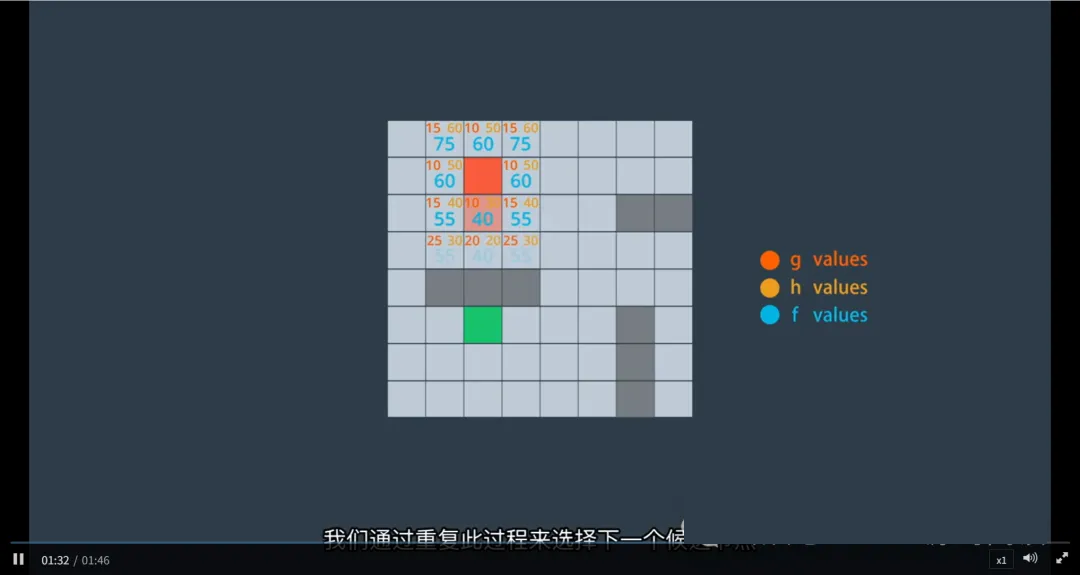
真实世界交叉路口决策

A*（A-Star）算法不仅用于简单的网格地图搜索，更被应用于真实道路网络的全局路径规划。通过将实际地图抽象为图结构，并结合成本评估模型，A*能够帮助无人车在复杂交通场景（如交叉路口）中做出最优行驶决策。

从真实地图到图结构：交叉路口的建模

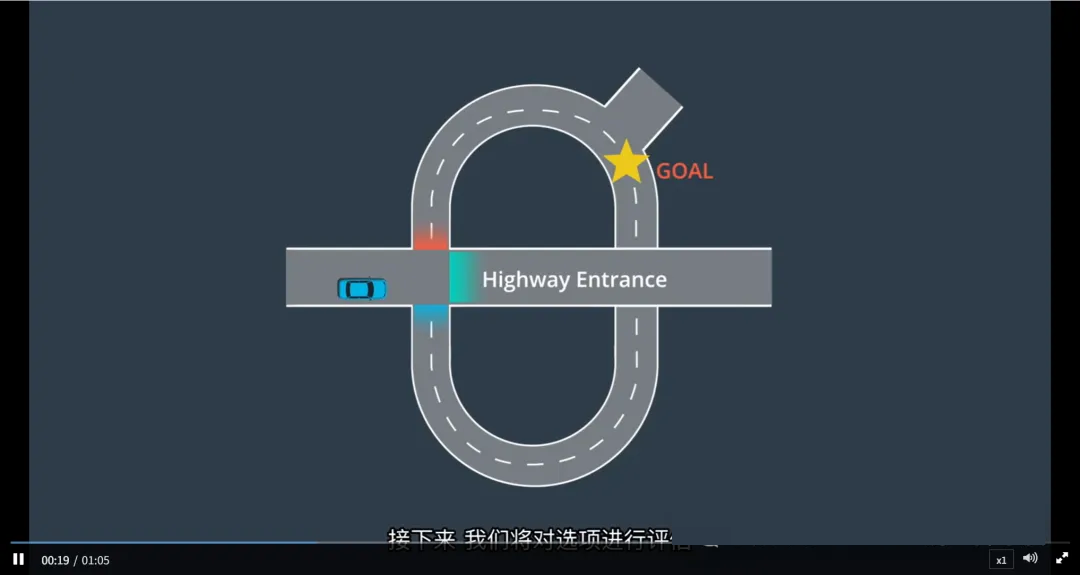
当无人车 approaching 一个交叉路口时，它面临多个行驶选择：

直行

左转

右转

Apollo首先将这个现实场景转换为图（Graph）数据结构：

节点（Nodes）：代表每条可行驶的道路或车道段

边（Edges）：表示车辆可以从当前道路转移到另一条道路的合法路径

在该交叉口处，系统生成三个候选节点，分别对应：

直行路线

左转路线

右转路线

这样，整个道路网络就被转化为一个带权图，供A*算法进行智能搜索。

成本评估：g值、h值与f值的综合判断

对于每一个候选路径（即每个候选节点），A*通过计算其 f值 = g值 + h值 来评估其“优劣”。

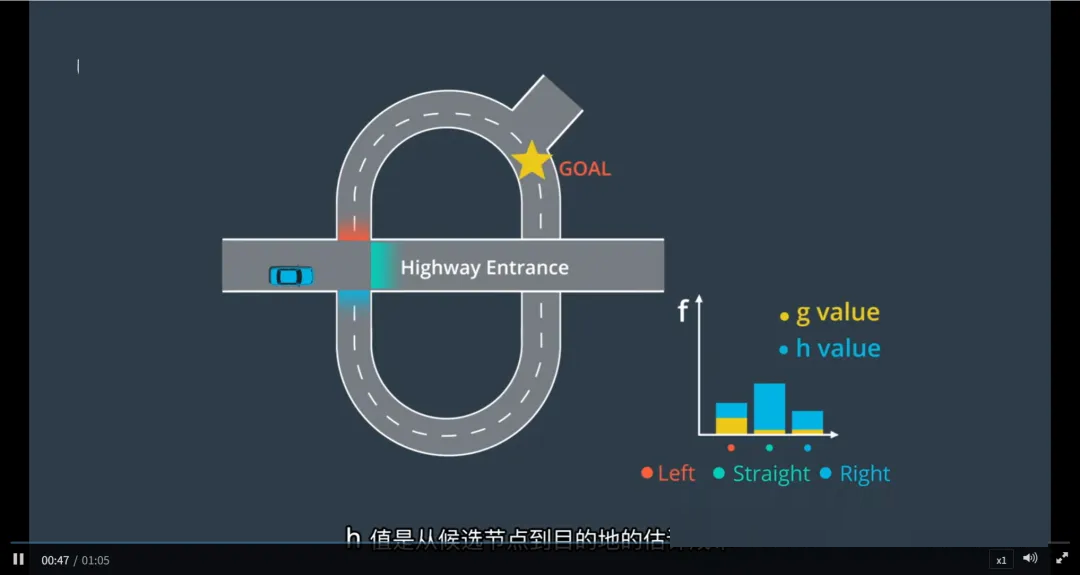
1. g(n)：从起点到候选节点的实际成本（已知代价）

表示从车辆当前位置到该候选路径终点所付出的代价

在交叉路口场景中：

直行：驾驶简单，时间短 → g 值较低

左转：需等待对向车流、信号灯，操作复杂 → 分配更高的 g 值

右转：相对容易，但仍比直行略复杂 → g 值适中

实践中，“拐过交叉路口很费劲”，因此转弯动作会被赋予更高的操作成本

2. h(n)：从候选节点到最终目的地的估计成本（启发式代价）

是一种启发式估算，通常基于距离、时间或通行难度

在评估各选项时发现：

某条路虽然当前可通过，但需要绕行很长距离才能返回目标方向

或者该道路通向高速公路出口后难以调头

因此，这类路径会被分配更高的 h 值

即使某条路目前畅通，若未来路径极不高效，也会被算法“提前淘汰”

3. f(n) = g(n) + h(n)：总评估值决定最优选择

Apollo对每个候选节点计算其 f 值：

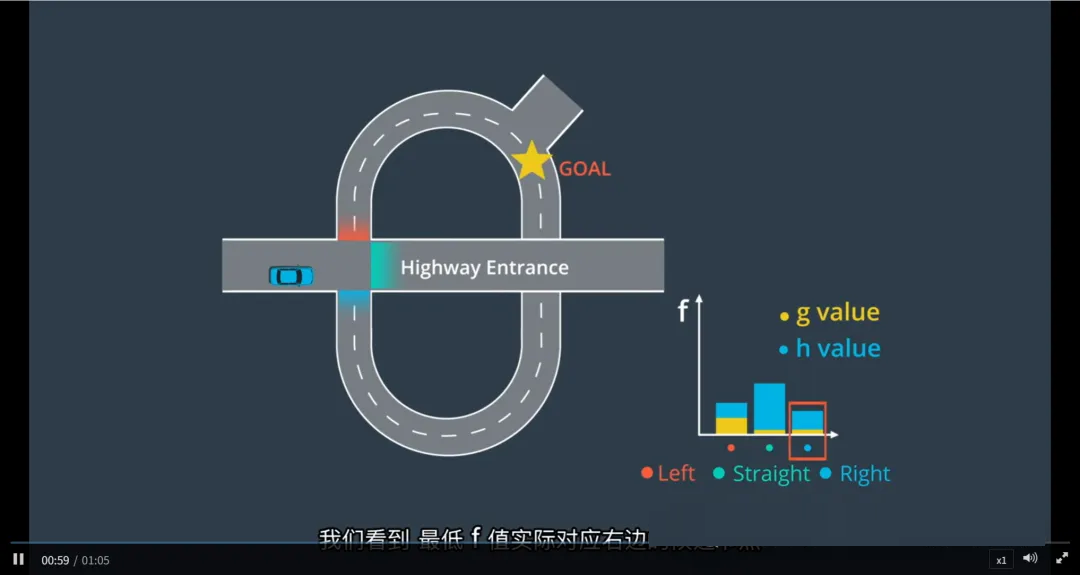
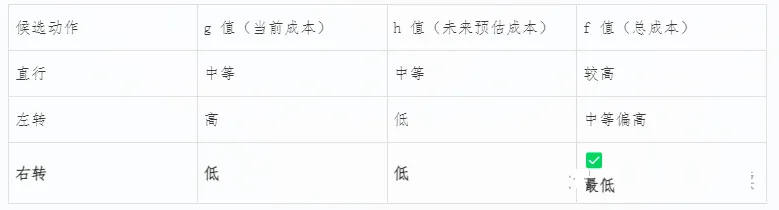
最终，系统选择 f 值最小的候选节点 —— 在本例中是右转路径，作为下一步的行驶方向。

决策背后的逻辑：平衡当下与未来

这一过程体现了A*算法的核心智慧：

不仅要考虑当前动作的难易程度（g值），还要预测该选择对未来路径的影响（h值）

例如：

虽然左转可能更接近直线方向（h值低），但因等待时间长（g值高），整体不划算

虽然某条路看似直达，但后续绕远严重（h值高），也不应选择

右转虽非最直接，但综合成本最低，是最优解

从规划到轨迹

高层级路线规划（宏观）

目标：从A点到B点，规划一条全局行驶路线

依赖：高精度地图、当前位置、目的地

输出：由道路和车道组成的路径（如导航所示）

特点：只考虑静态地图信息，不涉及实时障碍物

类似手机导航：“前方3公里右转进入主路”

低层级轨迹生成（微观）

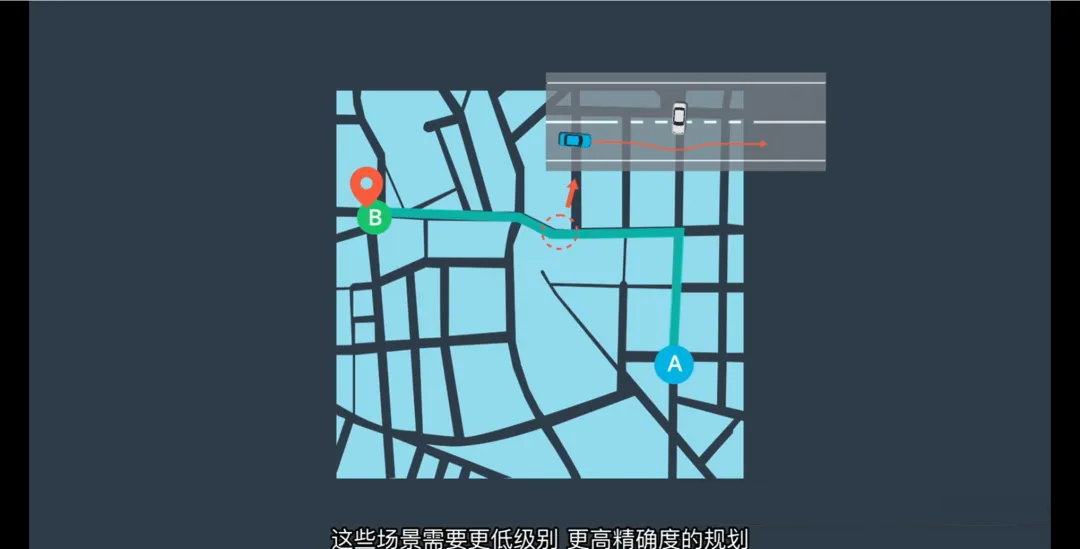
目标：在全局路线基础上，生成一条安全、舒适、可执行的行驶轨迹

挑战：处理地图中没有的动态物体，例如：

前方车辆掉头

慢速行驶的车辆

横穿的行人或自行车

输出：一系列带时间戳的轨迹点，包含位置、速度、加速度和到达时间

解决“如何安全通过具体场景”的问题

两者关系

路线规划告诉车“去哪”

轨迹生成告诉车“怎么去”

轨迹生成是在全局路线的指导下，结合实时感知与预测，进行精细化、高精度的动态调整

D轨迹

在自动驾驶中，轨迹生成不仅仅是规划一条空间路径，更是一个包含时间维度的动态过程。

轨迹生成的目标

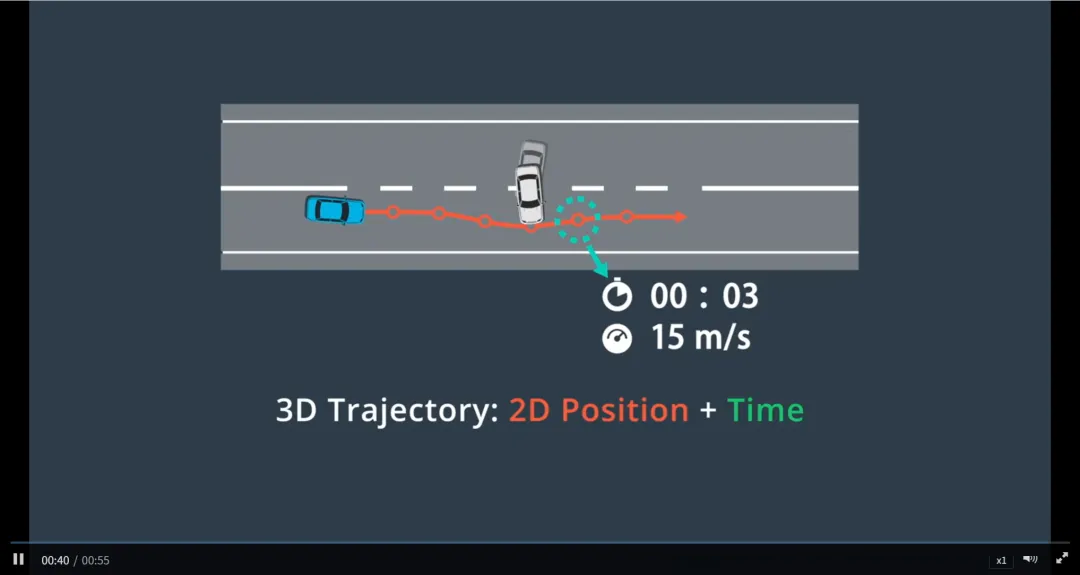
生成一条由一系列路径点（waypoints） 定义的平滑、安全、可执行的行驶轨迹。

每个路径点包含：

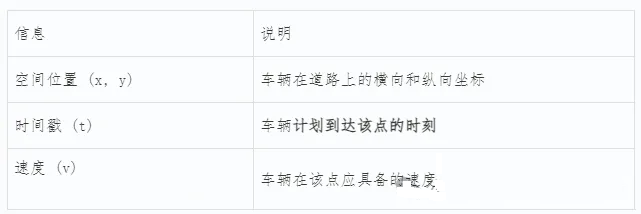
什么是“3D轨迹”？

这里的“3D”不是指三维空间（x, y, z），而是指：

两个空间维度 + 一个时间维度 = 3D轨迹

X 和 Y：车辆在地图中的平面位置

T（时间）：车辆到达该位置的精确时刻

这样，整条轨迹就不再是“从A到B的路线”，而是一条时空路径——它描述了“车辆在什么时间应该出现在什么位置”。

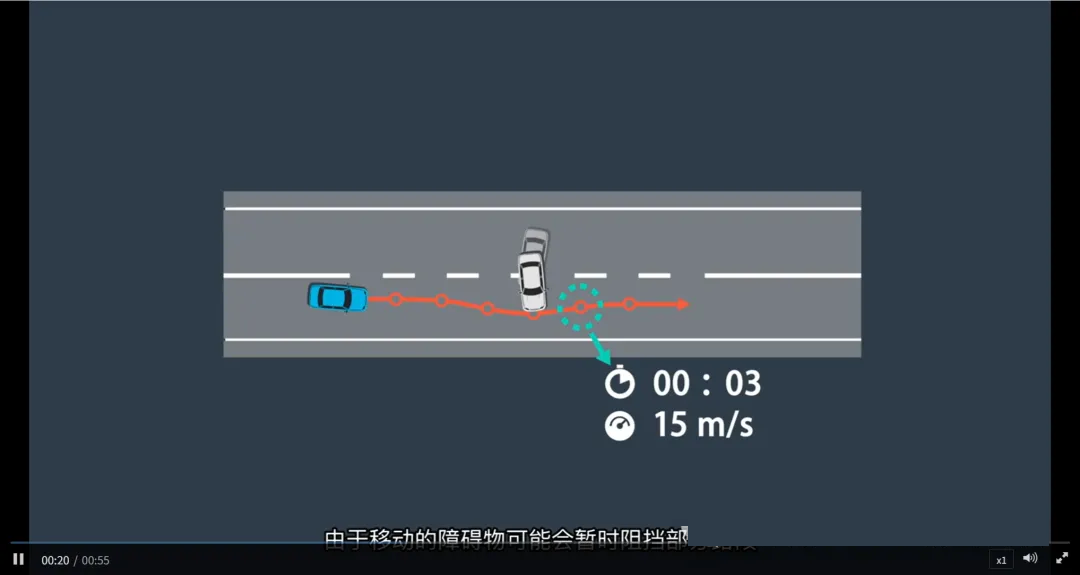
为何需要时间维度？

因为道路上存在动态障碍物（如其他车辆、行人），它们会随时间移动，可能暂时阻挡某些路段。

通过为每个路径点添加时间戳，我们可以：

结合预测模块的输出（知道其他物体未来何时出现在哪里）

确保：当我们的车辆计划通过某个点时，该点未被其他物体占用

实现真正的时空避障

举例：我们计划在 t=5s 时通过路口某点 → 检查预测结果发现一辆车将在 t=4.8~5.2s 占据该点 → 因此调整轨迹（提前或延后通过）

速度的作用

速度（v）用于控制车辆按时到达每个路径点

通过调节不同路段的速度（加速、减速、匀速），确保时间戳的准确性

速度也影响乘坐舒适性（避免急加减速）

评估一条轨迹

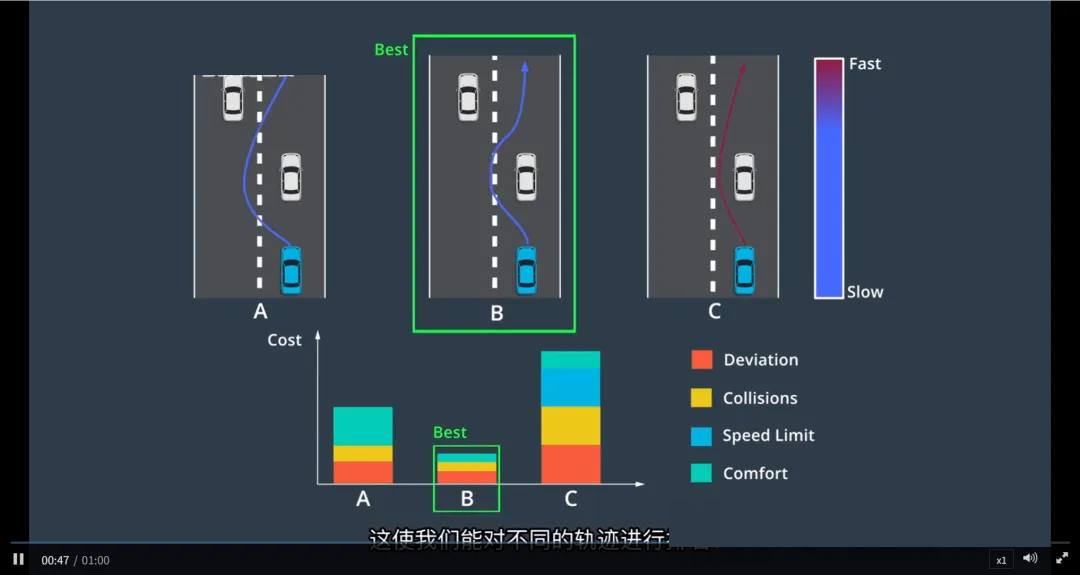
在自动驾驶中，生成一条轨迹只是第一步，如何评估并选择最优轨迹才是决策的关键。

Apollo系统通过综合考虑多重约束，并利用成本函数（Cost Function） 对候选轨迹进行评分和排序，最终选择最优行驶路径。

一条“好”轨迹的四大基本要求

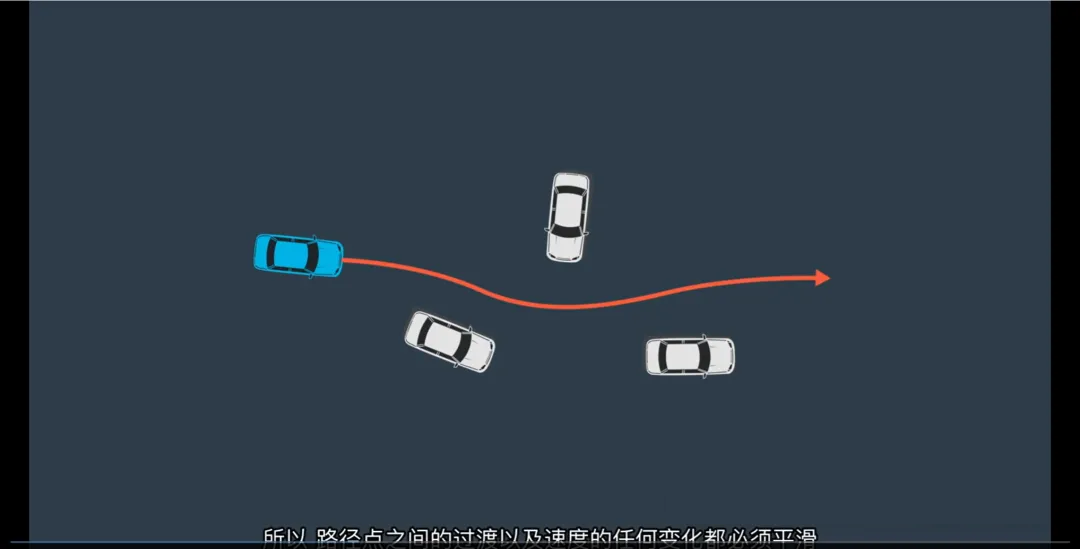
多条可行轨迹？如何选择最佳？

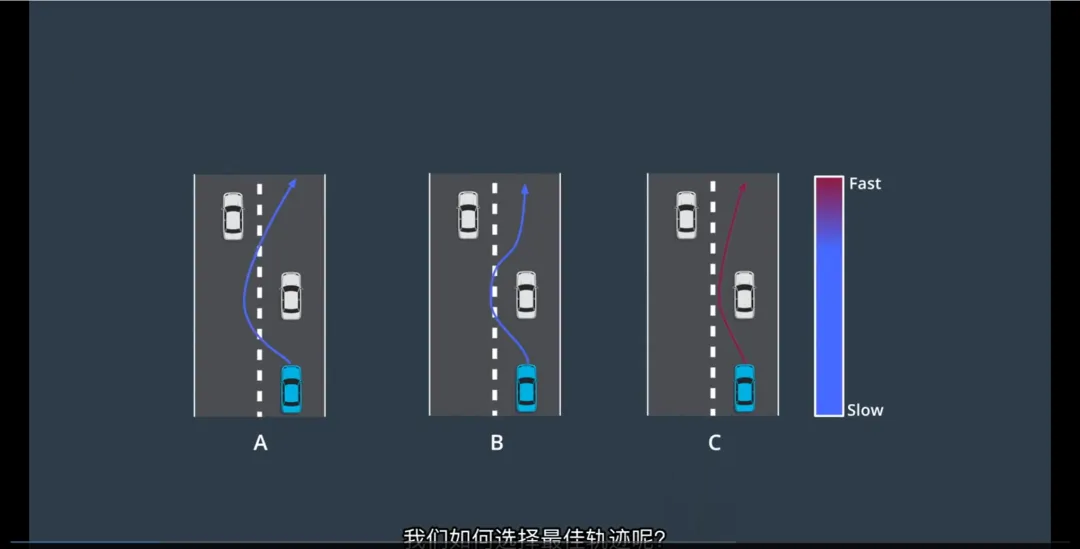
在实际驾驶中，两点之间可能存在多条满足上述条件的轨迹。例如：

沿车道中心线直行

稍微偏左以远离对向车流

提前减速准备变道

那么，哪一条最好？

答案是：使用 成本函数（Cost Function）

成本函数：给每条轨迹“打分”

成本函数是一种数学模型，它将轨迹的各种“缺陷”或“偏好”量化为数值惩罚（即“成本”），并汇总成一个总分。

常见的成本项包括：

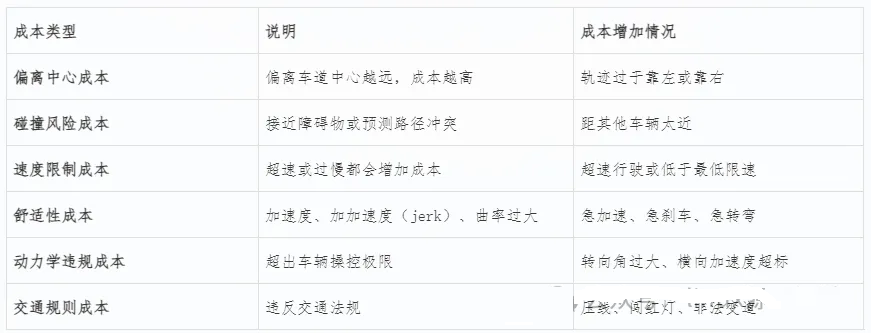
总成本 = 所有单项成本的加权和

轨迹选择流程

生成多条候选轨迹（如不同变道时机、不同速度曲线）

对每条轨迹计算总成本

选择成本最低的轨迹作为最终执行方案

类比：就像人类司机在多个安全选项中选择“最自然、最顺畅”的那一条。

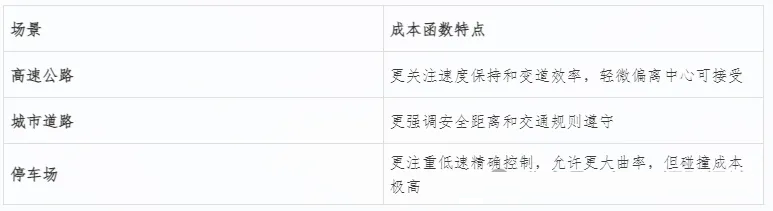
不同场景，不同“偏好”

Apollo会根据驾驶环境动态调整成本函数的权重：

Frenet坐标

在自动驾驶轨迹规划中，如何高效、直观地描述车辆与道路的关系至关重要。虽然我们常用笛卡尔坐标系（x, y） 来表示位置，但它在道路场景中存在明显局限。为此，百度Apollo等系统广泛采用 Frenet坐标系 作为更优的解决方案。

为什么笛卡尔坐标系不适合道路行驶？

在笛卡尔坐标系中，一个点的位置由 (x, y) 表示，但这对车辆来说不够直观：

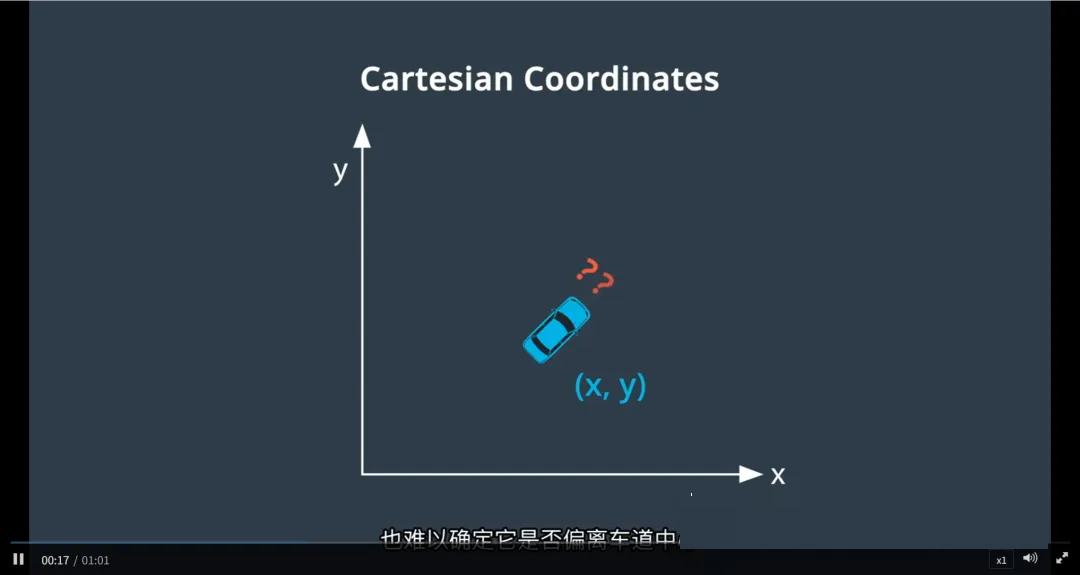
给出 (x=100, y=200)，无法直接判断：

车辆在道路上行驶了多远？

是否偏离车道中心？

是在直道还是弯道？

道路弯曲时，x 和 y 变化不均匀，难以衡量“沿道路前进”的距离

处理变道、跟车、超车等行为时，计算复杂且不直观

简言之：笛卡尔坐标是“地图视角”，而车辆需要“道路视角”

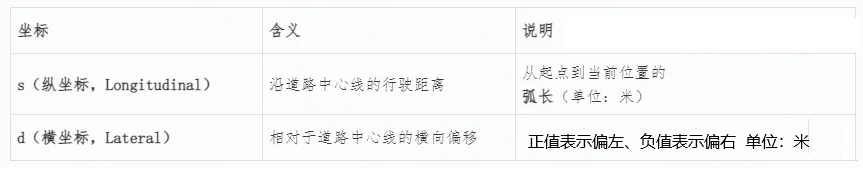
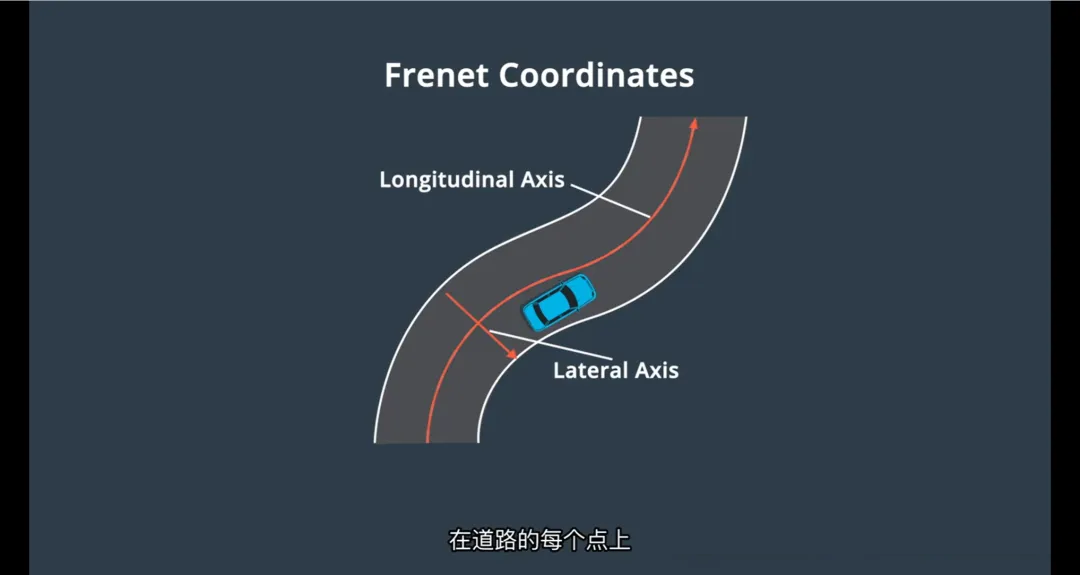
什么是Frenet坐标系？

Frenet坐标系是一种以道路为中心的局部坐标系，它将车辆的位置分解为两个关键维度：

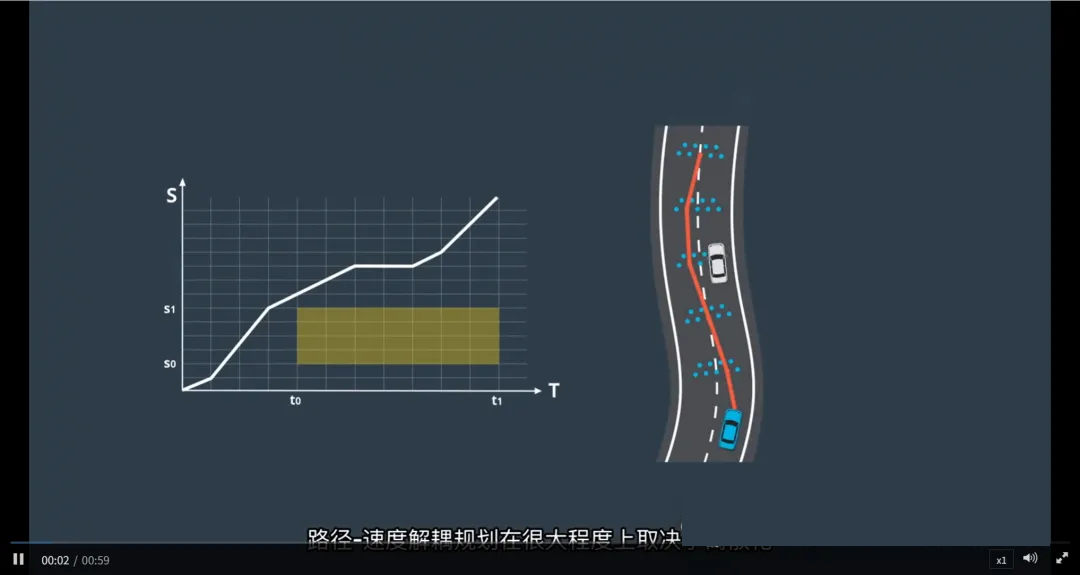
路径-速度解耦规划

在自动驾驶轨迹规划中，直接同时规划“走哪条路”和“以什么速度走”会带来极高的计算复杂度。为此，百度Apollo采用了一种高效且实用的策略：路径-速度解耦规划（Path-Speed Decoupling）。

该方法将复杂的三维轨迹规划问题分解为两个独立但有序的步骤：

第一步：路径规划（Path Planning）

目标：生成多条车辆可行驶的候选路径（空间曲线）

输入：起点、终点、障碍物信息、高精地图

过程：

在Frenet坐标系（s, d）或笛卡尔空间中生成多条平滑的候选路径

每条路径由一系列 (x, y) 或 (s, d) 点组成

评估与选择：

使用成本函数对每条路径打分，考虑因素包括：

路径平滑度（曲率是否过大）

安全性（是否靠近障碍物）

是否偏离车道中心

是否符合交通规则

按成本从低到高排序，选择成本最低的最优路径

第二步：速度规划（Speed Planning）

目标：为选定的路径生成一条最优的速度曲线

输入：最优路径、障碍物预测、交通信号、道路限速

过程：

将路径离散为一系列路径点

为每个点分配一个目标速度，形成速度序列（v₁, v₂, ..., vₙ）

这条序列称为速度曲线（Speed Profile）

优化与约束：

使用优化算法（如动态规划、二次规划）生成速度曲线

需满足多种限制：

不超速

加速度和加加速度（jerk）在舒适范围内

能安全避让动态障碍物（如前车减速）

遵守红绿灯（在红灯前停下）

路径生成与选择

在自动驾驶的路径-速度解耦规划框架中，路径规划阶段的核心任务是生成一组安全、平滑且可行的候选路径，并从中选出最优的一条。

路径规划的目标不是只生成一条路径，而是：

生成多条可能的行驶路径

评估每条路径的“好坏”

选择综合成本最低的最优路径

这一过程通常采用基于采样的路径生成方法。

路径生成步骤：

1. 路段分割：将道路划分为单元格

将待规划的前方道路在 Frenet坐标系（s, d） 或笛卡尔空间中划分为多个纵向段（s方向）

每个纵向段称为一个单元格（Cell），代表车辆在某一前进距离范围内的横向可行驶区域

2. 随机采样：在每个单元格中选取点

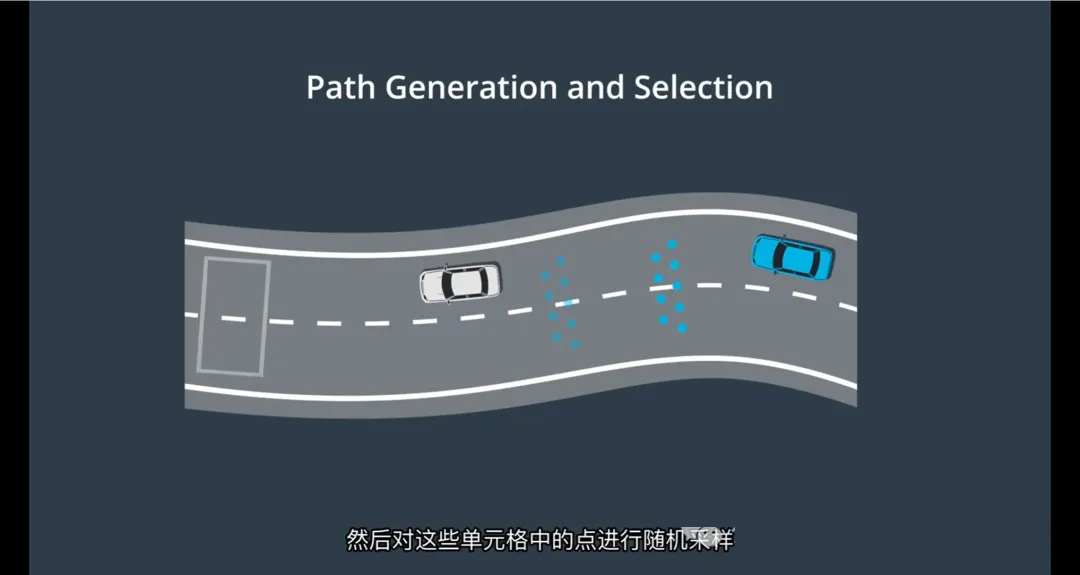
在每个单元格内随机采样一个或多个横向位置点（d值）

这些点代表车辆在该纵向位置可能经过的横向坐标

3. 连接成路径

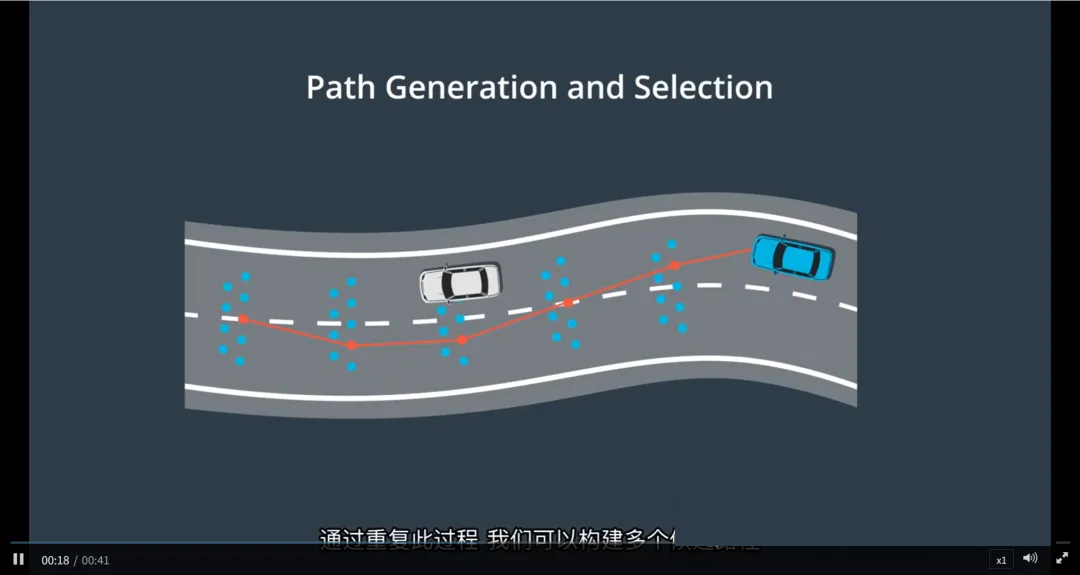
将从每个单元格中选出的一个点依次连接

形成一条从起点到终点的候选路径

通过重复采样和连接，生成多条不同的候选路径

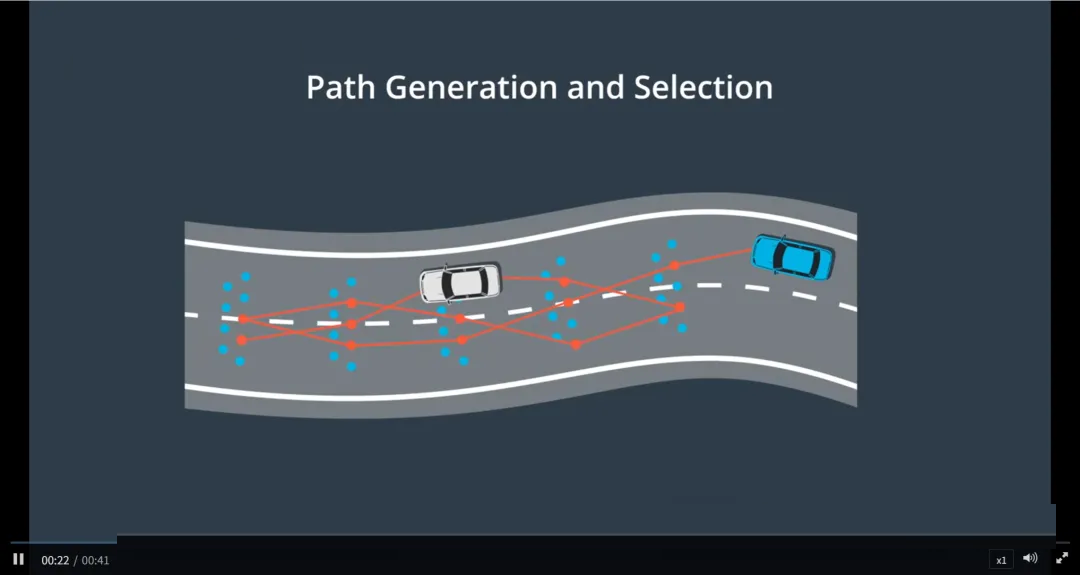
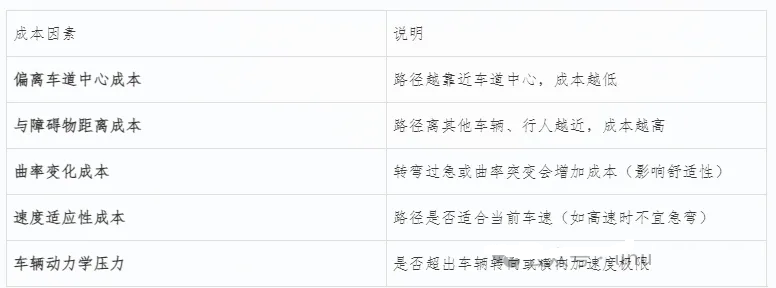
路径评估：使用成本函数打分

每条候选路径都会通过成本函数（Cost Function） 进行评分，成本越低，路径越优。

常见的成本项包括：

路径选择：选成本最低的路径

将所有候选路径按总成本从低到高排序

选择成本最低的路径作为最终的“最优路径”

这条路径将进入下一阶段：速度规划

ST图

在自动驾驶的路径-速度解耦规划中，完成路径规划后，下一步是为选定路径设计一条最优的速度曲线。为此，百度Apollo等系统使用一种直观而强大的工具——ST图。

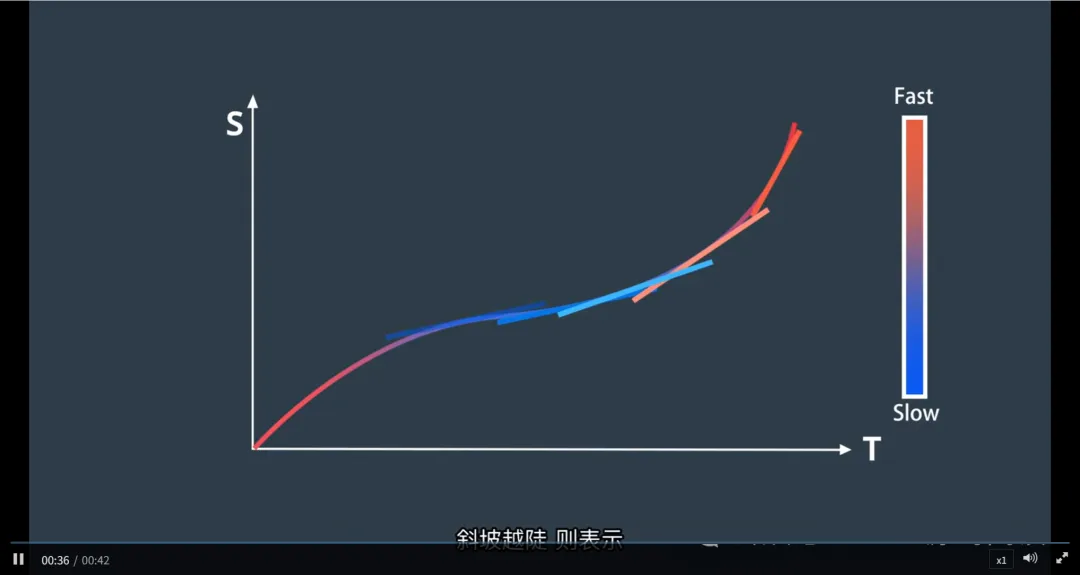
什么是ST图？

S：表示车辆沿道路中心线的纵向位移（单位：米）

来自Frenet坐标系中的 s 坐标

反映车辆在道路上“走了多远”

T：表示时间（单位：秒）

从规划起点开始计时

那么， ST图 是一个以 时间（T）为横轴、纵向位移（S）为纵轴 的二维坐标图。

ST曲线：车辆纵向运动的“时间线”

在ST图中，一条从原点出发的曲线称为 ST曲线，它完整描述了车辆的纵向运动：

曲线上每一个点 (t, s) 表示：“在时间 t，车辆应行驶到路径上的 s 位置”

通过斜率理解速度

速度（v） 是位移对时间的变化率：v = ds/dt

在ST图中，曲线的斜率 = 当前速度

斜率越大 → 单位时间内移动距离越长 → 速度越快

斜率越小 → 单位时间内移动距离越短 → 速度越慢

斜率为零（水平） → 位移不变 → 车辆静止（停车）

举例：

一条陡峭上升的直线 → 匀速高速行驶

一条平缓上升的直线 → 匀速低速行驶

一条水平线段 → 车辆在该时间段内停车（如等红灯）

ST图的核心作用：设计与评估速度曲线

1. 可视化车辆行为

直观展示车辆何时加速、减速、匀速、停车

便于分析是否满足交通信号、前车距离等约束

2. 避障规划

在ST图中，动态障碍物（如前车）也可表示为一条“障碍物轨迹”

规划的速度曲线必须避开这些障碍区域

例如：不能与前车的ST曲线相交，确保不追尾

3. 优化速度 profile

通过调整ST曲线的形状，优化：

行驶时间（尽快到达）

能耗（避免频繁加减速）

乘坐舒适性（控制加加速度）

速度规划

为了设计一条最优的速度曲线，我们需要将连续的ST图进行离散化处理，并在考虑各种限制条件的情况下，使用优化算法来寻找最佳路径。以下是该过程的关键步骤和概念：

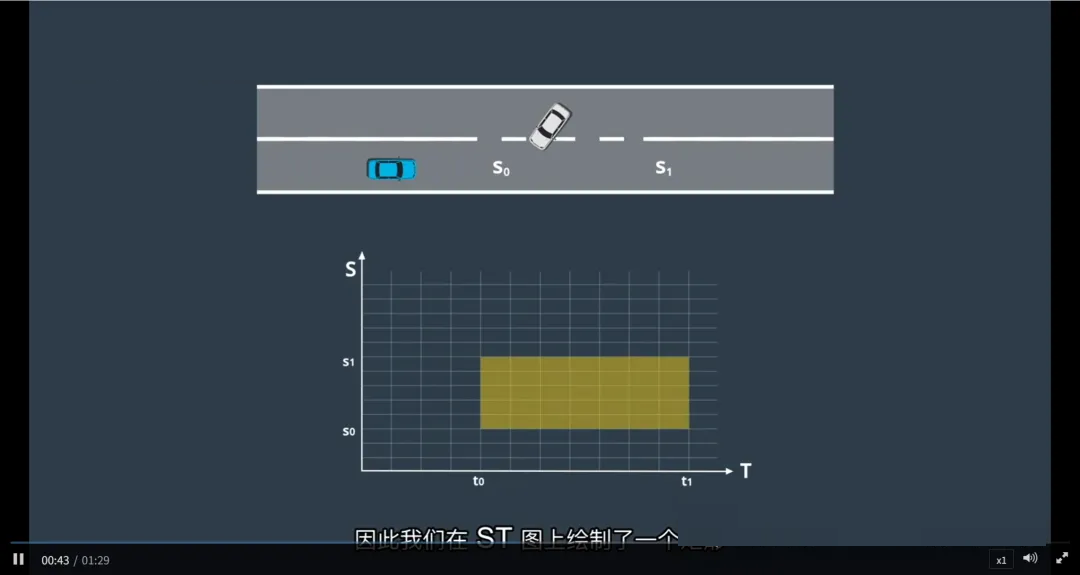
离散化ST图

单元格划分：

将ST图划分为多个小单元格，每个单元格代表一个时间间隔内的固定位移段。

在每个单元格内，假设车辆的速度保持不变，尽管相邻单元格之间的速度可能不同。

这种方法简化了速度曲线的构建过程，同时仍能保持对理想曲线的良好近似。

障碍物表示：

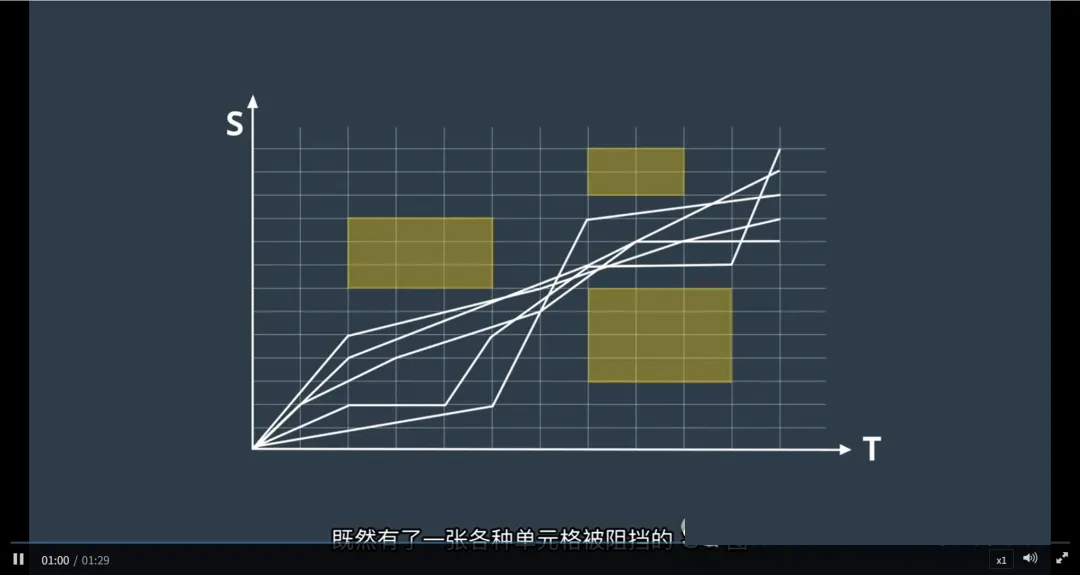
障碍物（如其他车辆、行人等）可以被绘制为ST图上的矩形区域。

如果预测到某个障碍物将在时间段 (t_0) 至 (t_1) 内占据位置 (s_0) 到 (s_1)，则在对应的ST图上绘制一个矩形，它会阻挡这段时间内的这部分道路。

速度曲线的设计必须避免与这些障碍物矩形相交，以防止碰撞。

优化引擎选择最佳速度曲线

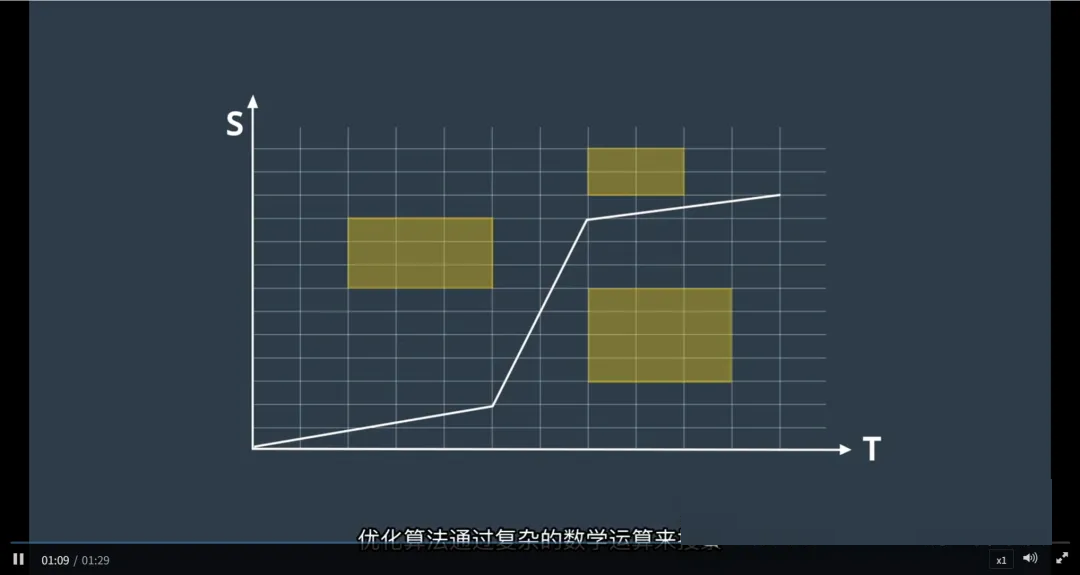
限制条件：

法律限制：例如速度上限，确保不超速。

距离限制：比如与前方障碍物保持安全距离。

物理限制：包括加速度、减速度的最大值，以及车辆的机械性能极限。

优化算法：

使用复杂的数学运算搜索满足上述所有限制条件下的低成本解决方案。

目标是找到既能保证行驶效率又能确保安全的最佳速度曲线。

这个过程涉及到平衡多种因素，如减少行程时间、提高乘客舒适度、遵守交通规则和保护车辆免受损害。

优化

路径-速度解耦规划是一种将复杂的轨迹规划问题简化为路径选择和速度曲线构建两个相对独立的子问题的方法。这种方法极大地依赖于离散化技术，下面是对这一过程及其优化方法的总结：

路径选择

离散化道路：首先需要将行驶的道路划分为多个单元格，每个单元格代表了一段特定的空间区域。

这种划分方式使得路径选择变得更加直观且易于处理。

速度曲线构建

ST图离散化：速度曲线的构建涉及到将时空（S-T）图进行离散化处理，即把时间间隔和空间位置一同考虑并划分成多个单元格。

在这些单元格中，假设速度保持不变，尽管相邻单元格间的速度可能不同。

尽管这种方法简化了原本复杂的问题，但其生成的轨迹并不平滑，因此需要进一步优化以适应实际应用的需求。

轨迹平滑化

为了改善由离散化导致的不平滑轨迹，可以采用二次规划技术：

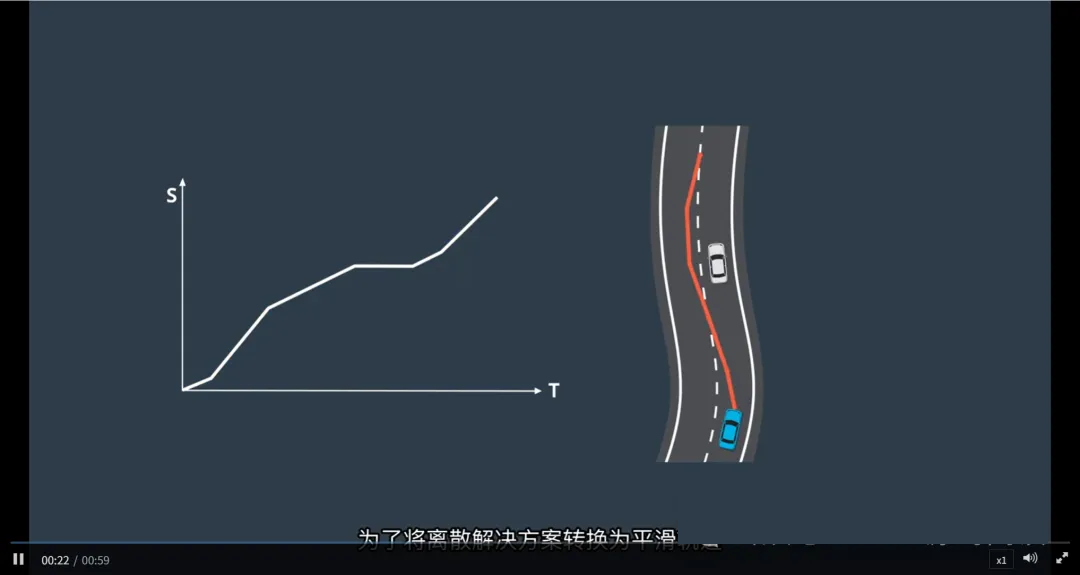
二次规划：通过使用二次规划技术，能够将一个平滑的非线性曲线拟合到那些分段式线性的轨迹上，从而产生更加自然和平滑的行驶路线。

尽管二次规划背后的数学原理较为复杂，但对于实际应用而言，我们不需要深入了解其细节，而是可以直接利用现有的优化工具包来实现这一目标。

实现工具

Apollo等优化方案：例如，由Apollo提供的优化方案就是一个很好的例子，它可以帮助我们将离散化的路径和速度曲线转换为一条连续、平滑的三维轨迹。

构建三维轨迹

一旦路径和速度曲线被确定下来，接下来就可以结合二者来构建一个完整的三维轨迹，该轨迹不仅考虑到了车辆在空间上的移动，还兼顾了其随时间变化的速度调整，确保了行车的安全性和效率。

综上所述，路径-速度解耦规划通过离散化简化了轨迹规划问题，并借助二次规划等优化手段实现了从离散到平滑轨迹的转化，最终支持生成既安全又高效的行车路径。

路径-速度规划的轨迹生成

在自动驾驶系统中，路径-速度解耦规划是一种高效且实用的轨迹生成方法。以下是该流程的完整端到端回顾，基于上述的笔记再次进行了梳理。

场景描述

车辆正在道路上行驶，感知系统检测到前方有一辆慢速行驶的车辆，且距离正在逐渐缩小。为安全超车或避让，系统需生成一条新的行驶轨迹。

路径-速度解耦规划四步流程

生成候选路径（Path Generation）

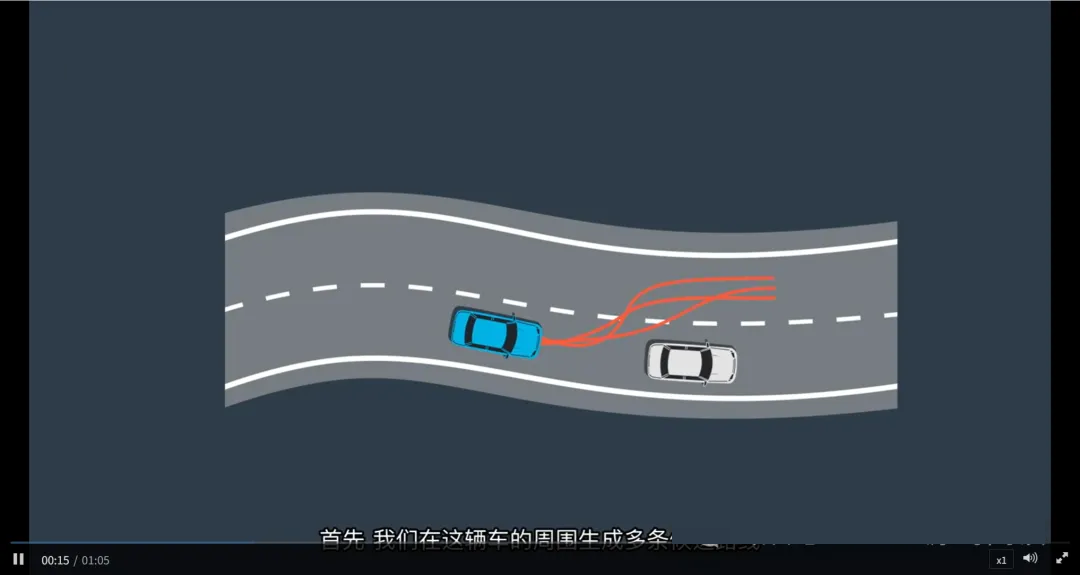
在当前车辆周围（如左侧变道区域）生成多条候选行驶路径

每条路径代表一种可能的行驶行为（如保持直行、向左偏移、完全变道）

路径通过在Frenet坐标系中对道路进行单元格划分并采样连接点生成

路径评估与选择（Path Selection）

使用成本函数对每条候选路径打分，考虑因素包括：

是否偏离车道中心

与障碍物的安全距离

路径曲率和平滑度

车辆动力学压力

选择成本最低的路径作为最优路径

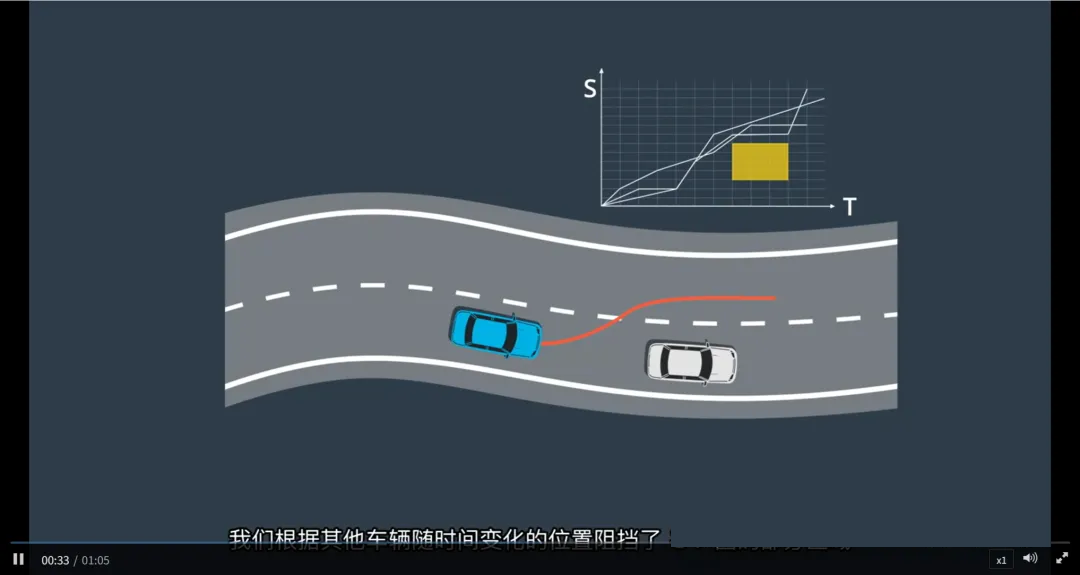
基于ST图的速度规划（Speed Planning）

在选定路径的基础上，构建ST图（S：纵向位移，T：时间）

将动态障碍物（如前车）投影为ST图中的阻挡矩形区域

例如：前车在时间 t₀ 到 t₁ 占据 s₀ 到 s₁ → 绘制一个矩形

使用优化引擎（如动态规划或二次规划）搜索一条不与障碍物相交的速度曲线

速度曲线受多种约束限制：

速度上限（交通法规）

加减速能力（车辆物理限制）

乘客舒适性（加加速度限制）

轨迹平滑与合成（Trajectory Smoothing & Merging）

由于离散化处理，初始路径和速度曲线可能不够平滑

使用二次规划（Quadratic Programming, QP） 对路径和速度曲线进行平滑优化

将平滑后的路径与优化后的速度曲线合并，生成最终的3D时空轨迹

轨迹可视化：颜色表示速度

在可视化中，轨迹常通过颜色编码速度：

红色：高速段（如超车加速）

蓝色：低速段（如减速避让或等待）

这种颜色映射帮助工程师直观判断车辆行为是否合理

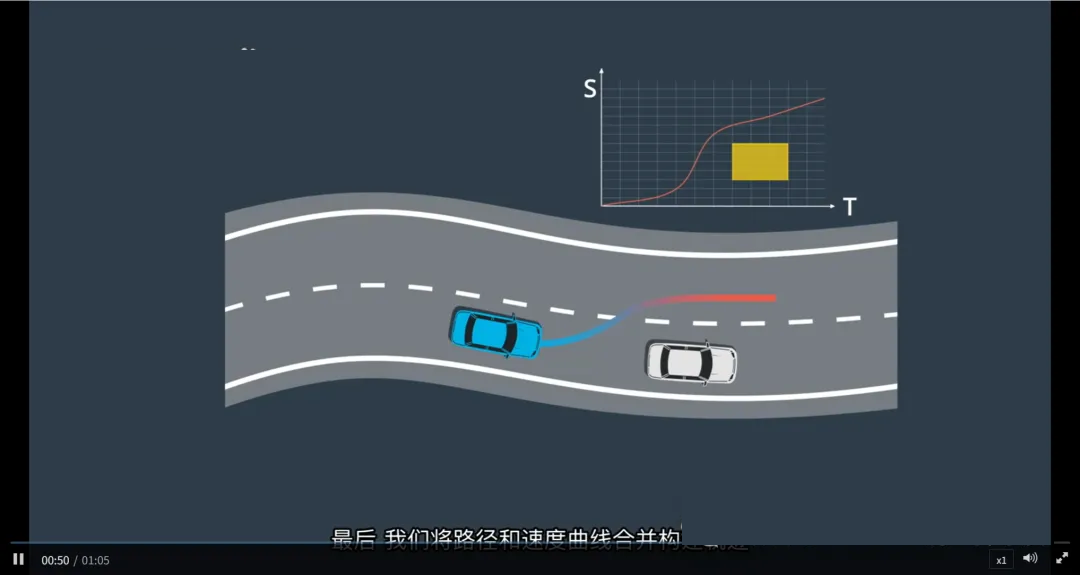
最终目标：安全、智能驾驶

通过上述流程，系统生成了一条：

免碰撞（避开前车ST障碍区）

舒适平滑（QP优化后无突变）

合法可行（符合交通规则和车辆能力）

动态响应（实时适应前方车辆）

的完整轨迹，车辆据此安全绕行慢车，继续行驶。

Lattice规划

Lattice规划（Lattice Planner）是百度Apollo等自动驾驶系统中一种高效、模块化的轨迹生成方法。它利用Frenet坐标系将复杂的三维轨迹规划问题解耦为两个独立的二维子问题，从而实现快速、安全、平滑的路径与速度规划。

核心思想：分而治之

在三维时空（纵向、横向、时间）中直接规划完整轨迹计算复杂。Lattice规划通过路径-速度解耦 + 空间分解，将问题拆解为：

一个纵向问题（ST） + 一个横向问题（SL）

然后分别求解，最后合并成最终轨迹。

坐标基础：Frenet坐标系

Lattice规划依赖于Frenet坐标系来描述车辆相对于道路的位置：

s（纵坐标）：沿道路中心线的行驶距离

d（横坐标）：相对于车道中心线的横向偏移

t（时间）：规划的时间维度

在此基础上，轨迹被分解为：

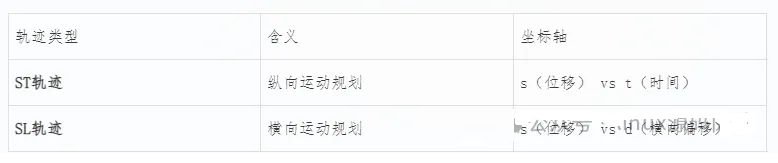
注意：这里的“L”其实是“d”，即横向位置，SL轨迹也可理解为 s-d 轨迹

Lattice规划两大步骤

第一步：分别生成 ST 和 SL 轨迹

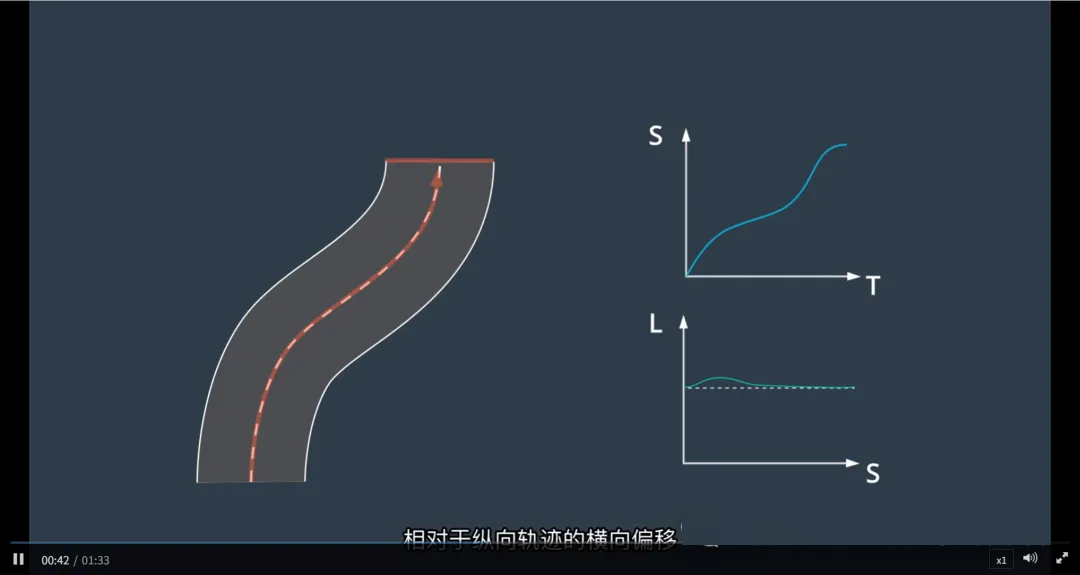
1. 纵向规划（ST 轨迹）

目标：决定“何时走多远”

方法：

将车辆初始状态（s₀, v₀, a₀, t₀）投影到 ST图

在不同时间点（如 t₁, t₂）上，对多个候选终点状态（s_end, v_end）进行采样

为每组初始→终点状态生成一条纵向轨迹（如多项式曲线）

使用成本函数评估每条轨迹，选择成本最低者

考虑因素：

速度限制

前车ST障碍区（避免相交）

加减速舒适性

2. 横向规划（SL 轨迹）

目标：决定“如何横向移动”（如保持居中、变道）

方法：

将车辆初始横向状态（d₀, d'₀, d''₀）投影到 SL图（即 s-d 图）

对多个候选横向终点状态（如 d_end = 0 表示居中，d_end = 3.5 表示左变道）

为每组状态生成横向轨迹（如五次多项式）

使用成本函数评估，选择最优

考虑因素：

与车道线的距离

与障碍物的横向安全距离

横向加速度和曲率舒适性

第二步：合并 ST 与 SL 轨迹

将最优的 ST轨迹（s-t） 和最优的 SL轨迹（s-d） 进行时间对齐与插值

通过查找每个时间点 t 对应的 s，再查找该 s 对应的 d

最终生成一条完整的 3D时空轨迹：包含 (t, s, d) 或转换为笛卡尔坐标 (t, x, y)

总结：Lattice规划流程图

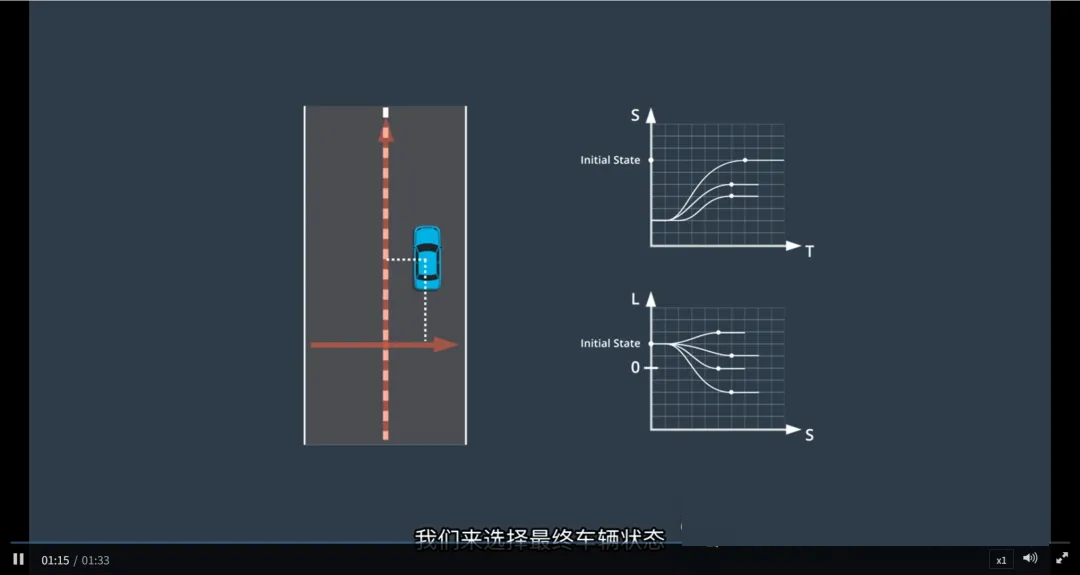
ST轨迹的终止状态

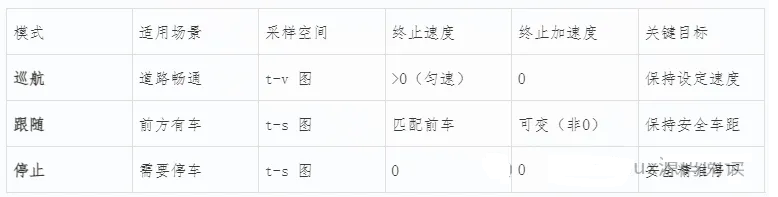
在Lattice规划中，生成纵向（ST）轨迹的关键一步是确定车辆在规划周期结束时的“终止状态”。根据不同的驾驶场景，这些终止状态被分为三类典型模式：巡航（Cruise）、跟随（Follow）和停止（Stop）。每种模式对应不同的采样策略和物理约束。

为什么需要定义终止状态？

Lattice规划通过状态采样生成候选轨迹。为了减少计算量并保证行为合理性，系统不会穷举所有可能，而是从预定义的行为模式中采样终点状态，再反向生成从当前状态到目标状态的平滑轨迹。

三种ST轨迹终止状态详解

1. 巡航模式（Cruise）

场景：前方无车，道路畅通，车辆可按期望速度行驶

目标：规划结束后，车辆进入匀速直线行驶状态

采样方式：

在 时间-速度图（t-v图） 上对点进行采样

每个采样点代表：在时间 t 达到速度 v

终止状态参数：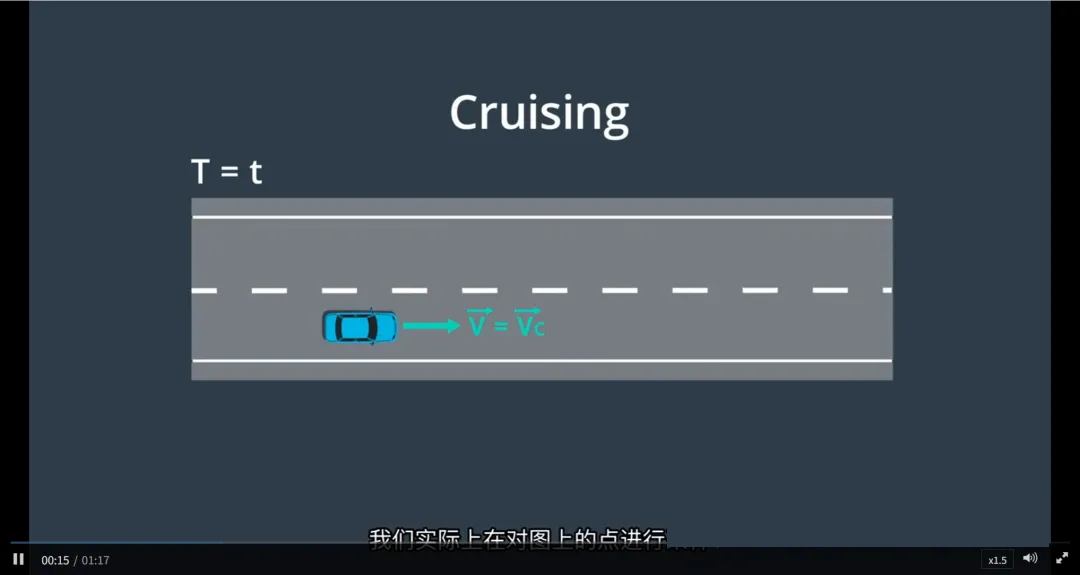

速度：v > 0（通常为道路限速或设定巡航速度）

加速度：a = 0（匀速行驶）

位置：由 s(t) 决定

特点：

轨迹终点加速度为0，确保平稳进入巡航

适用于自由流交通场景

2. 跟随模式（Follow）

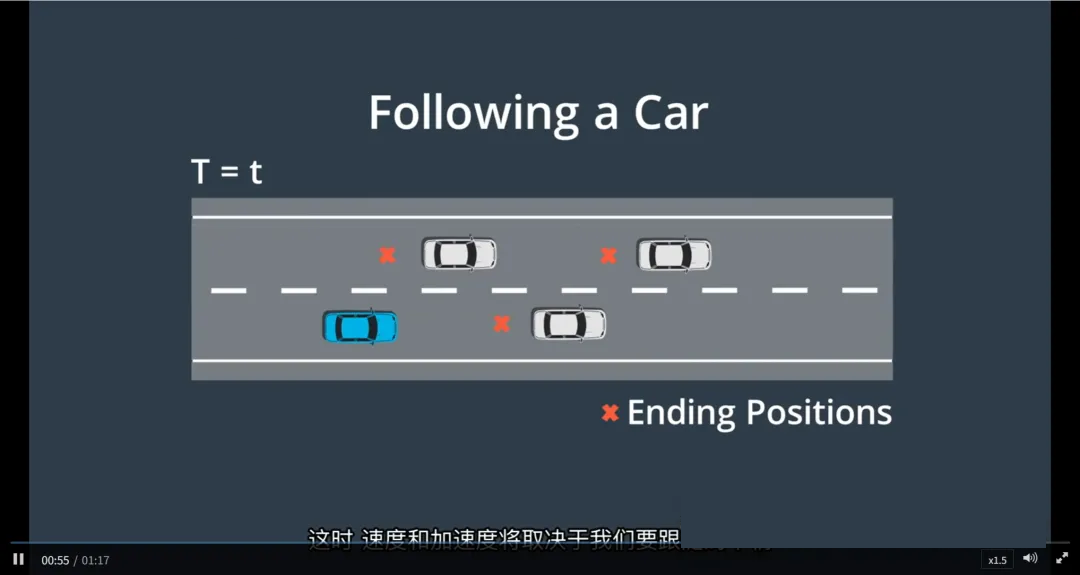
场景：前方有车，需保持安全距离跟行

目标：在指定时间到达前车后方的安全距离处

采样方式：

在 时间-位置图（t-s图） 上对点进行采样

每个采样点代表：在时间 t 到达位置 s

位置 s 设置为：前车位置 - 安全距离

终止状态参数：

速度：与前车当前速度一致（或略低）

加速度：动态调整，以维持车距

加速度不为0，可能正在减速或加速以匹配前车

特点：

速度和加速度由前车行为决定

需结合预测模块获取前车未来轨迹

安全距离通常基于相对速度动态计算（如 车距 = 1.5秒法则）

3. 停止模式（Stop）

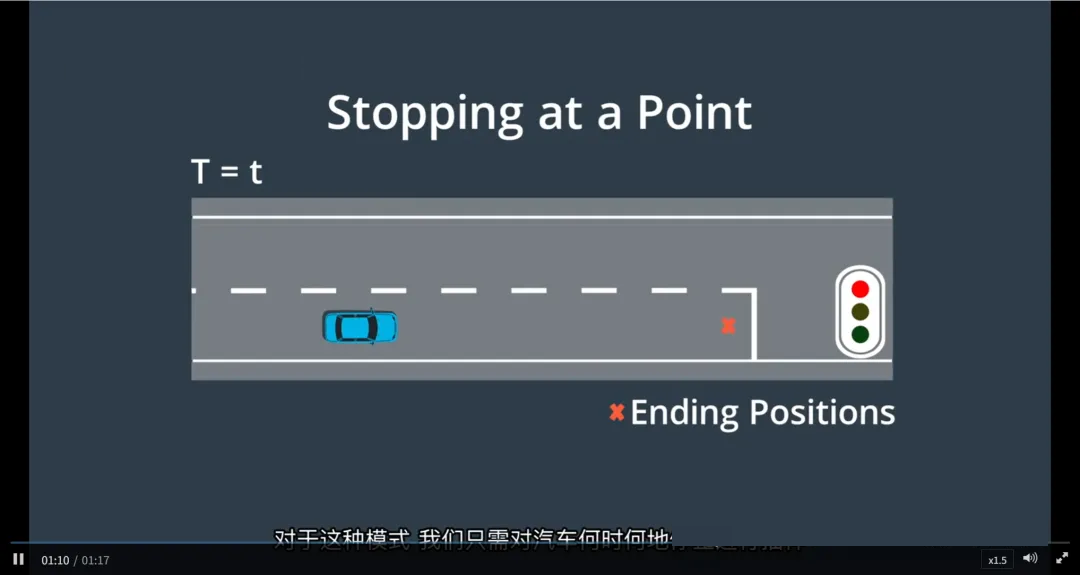
场景：前方有障碍、红灯、停车标志或交通拥堵

目标：在指定位置和时间安全停车

采样方式：

对“何时停、在哪停”进行采样

例如：在红灯前 s=50m 处，于 t=4s 时完全停下

终止状态参数：

速度：v = 0

加速度：a = 0（完全静止，非减速中）

位置：精确采样至停车线或障碍物前

特点：

轨迹终点速度和加速度均为0

需保证减速过程平滑，避免急刹

常用于交叉路口、收费站等场景

总结：三种模式对比

SL轨迹的终止状态

在Lattice规划中，SL轨迹（s-d 轨迹）负责规划车辆在横向（d方向）上的运动行为，例如：保持车道、变道、避障等。为了确保驾驶行为的安全与平稳，SL轨迹的终止状态遵循一个核心原则：

无论车辆经历何种横向操作，最终都应稳定地与车道中心线对齐，沿车道直行。

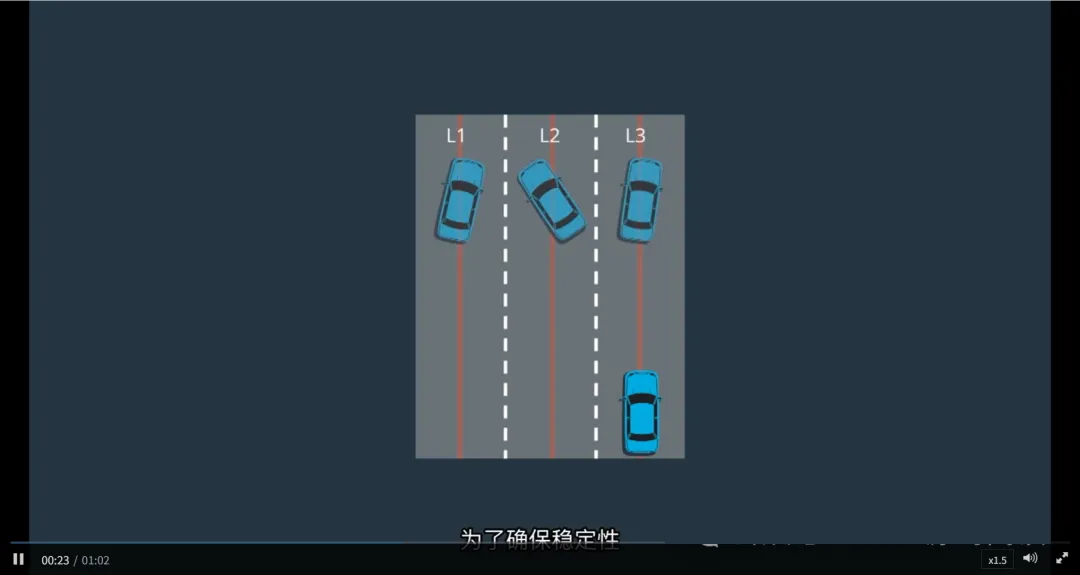
SL轨迹的目标：平稳回归车道

与纵向（ST）轨迹关注“何时走多远”不同，SL轨迹关注的是：

车辆如何从当前横向位置（如车道中央、偏左、偏右）移动到目标位置

如何在完成变道、避让等操作后，平滑、稳定地回归并保持在车道中心

为此，系统在规划SL轨迹时，对终止状态施加了严格的约束。

SL轨迹终止状态的关键条件

为了实现“稳定对齐车道中心”，车辆在轨迹终点必须满足以下条件：

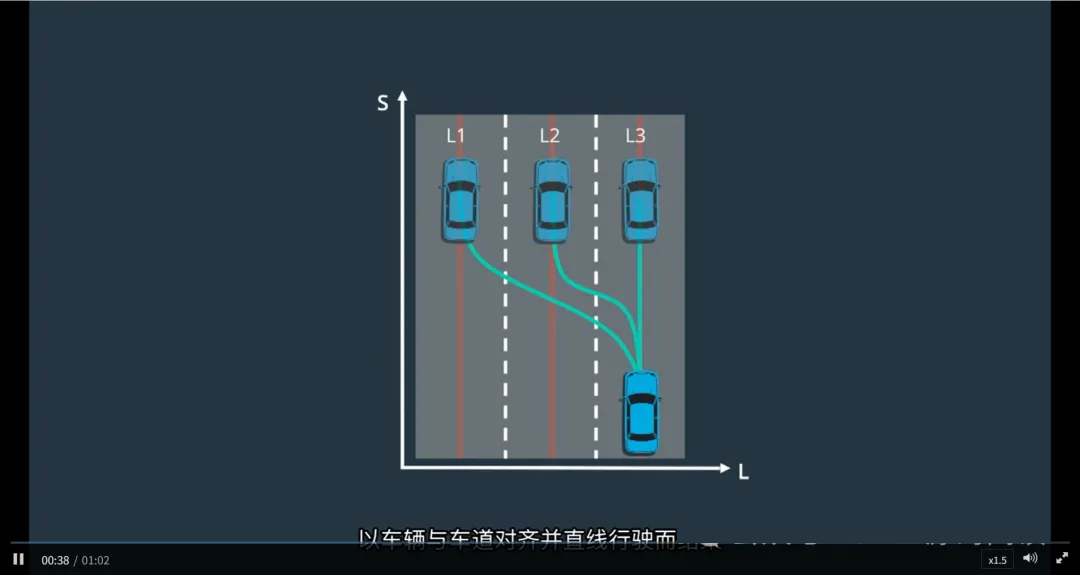
这意味着：车辆已完全完成变道或避让动作，正沿车道直线行驶，无任何侧向运动趋势。

终止状态的采样策略

采样范围小：只在相邻车道中心线附近进行横向位置采样

例如：当前车道 d=0，左邻道 d≈+3.5m，右邻道 d≈-3.5m

不采样任意d值：避免生成“停在车道边缘”或“斜着行驶”等不稳定状态

目标明确：所有候选轨迹的终点都指向“居中 + 直行”的理想状态

Lattice规划的轨迹生成

在Lattice规划中，轨迹生成的核心思想是将复杂的三维轨迹规划问题解耦为两个二维子问题：纵向规划（ST）和横向规划（SL）。当这两个独立的轨迹生成完成后，下一步是将它们重新融合，构建出一条完整的、可执行的3D时空轨迹。

轨迹生成流程回顾

路径-速度解耦：将轨迹规划分解为纵向（s-t）和横向（s-d）两个维度

分别生成：

ST轨迹：描述车辆在不同时间 t 应行驶的纵向位移 s

SL轨迹：描述在不同纵向位置 s 时，车辆应具备的横向偏移 d

最终目标：将ST和SL轨迹合并，生成最终的 3D轨迹（包含时间、x、y、速度等）

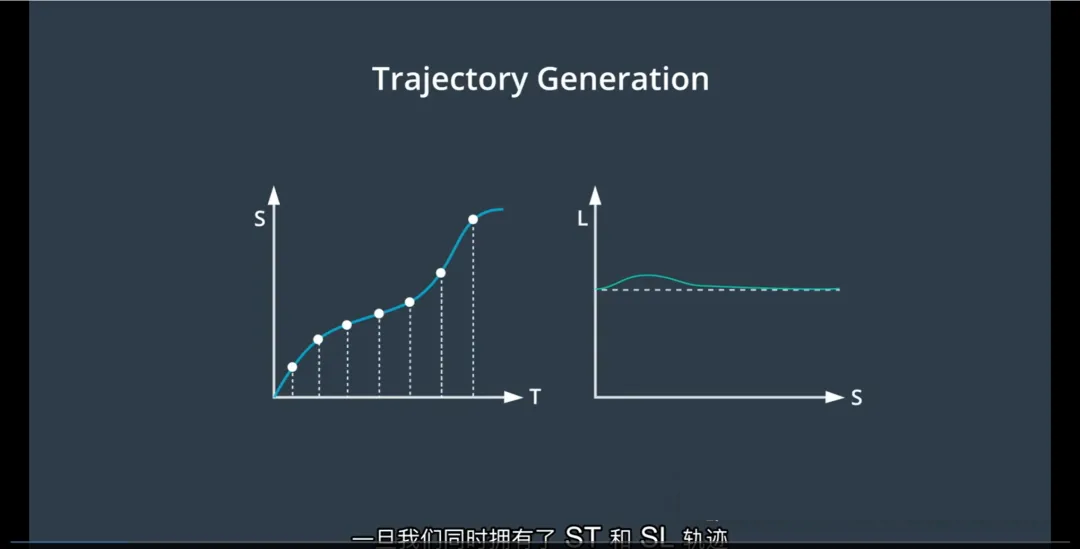
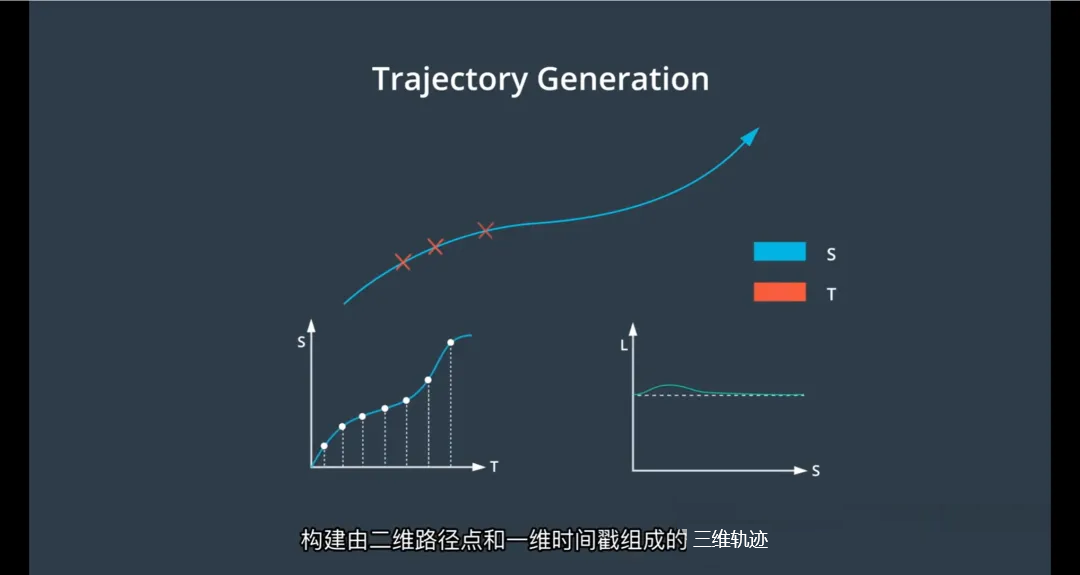
如何合并ST与SL轨迹？

合并的关键在于：两个轨迹共享同一个纵向坐标 s

合并步骤：

对齐纵向坐标 s

ST轨迹提供一组 (t, s) 点对：表示“在时间 t，车辆应到达位置 s”

SL轨迹提供一组 (s, d) 点对：表示“在位置 s，车辆应横向偏移 d”

按 s 值进行匹配

遍历ST轨迹中的每个 (t, s) 点

在SL轨迹中查找对应 s 值的横向偏移 d

如果没有精确匹配，使用插值（如线性或样条插值）计算 d

生成 (t, s, d) 三元组

每个点现在包含：

时间 t

纵向位移 s

横向偏移 d

这就构成了完整的Frenet坐标系下的3D轨迹

转换为笛卡尔坐标系 (x, y)

利用高精地图中的参考线（Reference Line）

将每个 (s, d) 点通过几何变换映射为全局 (x, y) 坐标

参考线提供了从道路弧长 s 到笛卡尔坐标的映射关系

输出最终轨迹

每个轨迹点包含：

时间戳 t

位置 (x, y)

速度 v

加速度 a

航向角 θ

这条轨迹可直接交由控制模块执行

通过这种“分而治之 + 精准融合”的策略，Lattice规划实现了高效、安全、平滑的自动驾驶轨迹生成。