| 编辑推荐: |
本文首先介绍Keras基础、Keras的模块结构、使用Keras搭建一个神经网络、主要概念等相关内容。
本文来自于博客园,由火龙果软件Anna编辑、推荐。 |
|
1.卷积与神经元
1.1 什么是卷积?
简单来说,卷积(或内积)就是一种先把对应位置相乘然后再把结果相加的运算。(具体含义或者数学公式可以查阅相关资料)
如下图就表示卷积的运算过程:
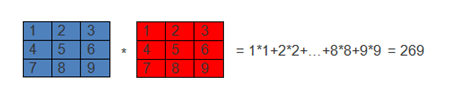
(图1)
卷积运算一个重要的特点就是,通过卷积运算,可以使原信号特征增强,并且降低噪音.
1.2 激活函数
这里以常用的激活函数sigmoid为例:
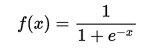
把上述的计算结果269带入此公式,得出f(x)=1
1.3 神经元
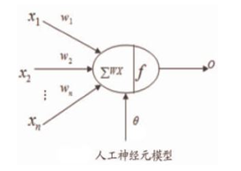
如图是一个人工神经元的模型:
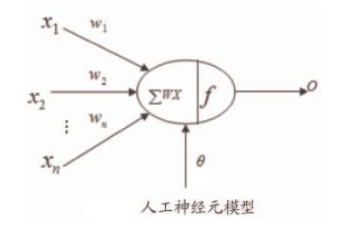
(图2)
对于每一个神经元,都包含以下几部分:
x:表示输入
w:表示权重
θ:表示偏置
∑wx:表示卷积(内积)
f :表示激活函数
o:表示输出
1.4 图像的滤波操作
对于一个灰度图片(图3) 用sobel算子(图4)进行过滤,将得到如图5所示的图片。
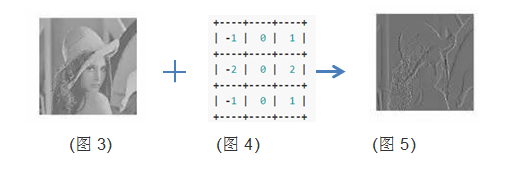
1.5小结
上面的内容主要是为了统一一下概念上的认识:
图1的蓝色部分、图2中的xn、图3的图像都是神经元的输入部分;图1的红色部分数值值、图2的wn值、图4的矩阵值都可以叫做权重(或者滤波器或者卷积核,下文统称权重)。而权重(或卷积核)的大小(如图4的3×3)叫做接受域(也叫感知野或者数据窗口,下文统称接受域)
2.卷积神经网络
在介绍卷积神经网络定义之前,先说几种比较流行的卷积神经网络的结构图。
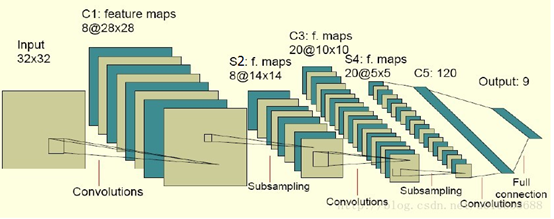
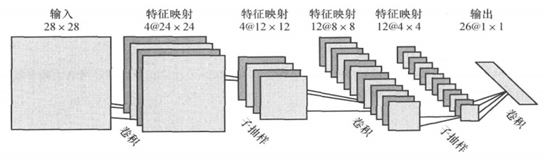
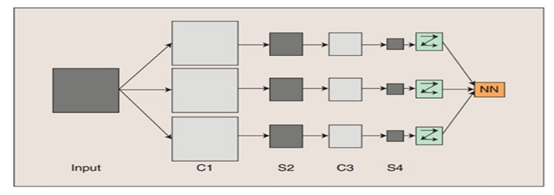
2.1 常见的几种卷积神经网络结构图
(图6)
(图7)
(图8)
(图9)
图8中的C-层、S-层是6中的Convolutions层和subsampling层的简写,C-层是卷积层,S-层是子抽样和局部平均层。在图6和图7中C-层、S-层不是指具体的某
一个层,而是指输入层和特征映射层、特征映射层和特征映射层之间的计算过程,而特征映射层则保持的是卷积、子抽样(或下采样)和局部平均的输出结果。而图
6和图7的区别在于最终结果输出之前是否有全连接层,而有没有全连接层会影响到是否还需要一个扁平层(扁平层在卷积层和全连接层之间,作用是多维数据一维化)。
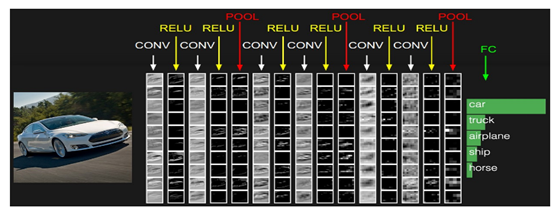
图9中CONV层是卷积层(即C-层),但是新出现的RELU层和POOL层是什么呢?RELU层其实是激活层(relu只是激活函数的一种,sigmoid/tanh比较常见于全连接层,relu常见于卷积层),为什么会多出来一个激活层呢?请看下图:
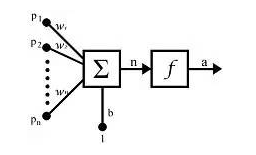
(图10)
(图2,方便对比复制了过来)
神经元的完整的数学建模应该是图10所示,与图2相比,把原来在一起的操作拆成了两个独立的操作:∑wx(卷积)和f(激活),因此多出了一个激活层。所以,在Keras中组建卷积神经网络的话,即可以采用如图2的方式(激活函数作为卷积函数的一个参数)也可采用图10所示的方式(卷积层和激活层分开)。激活层不需要参数。
Pool层,即池化层,其作用和S-层一样:进行子抽样然后再进行局部平均。它没有参数,起到降维的作用。将输入切分成不重叠的一些
n×n 区域。每一个区域就包含个值。从这个值计算出一个值。计算方法可以是求平均、取最大 max 等等。假设
n=2,那么4个输入变成一个输出。输出图像就是输入图像的1/4大小。若把2维的层展平成一维向量,后面可再连接一个全连接前向神经网络。
从图7可以看出,无论是卷积层还是池化层都可以叫做特征映射层,而两层之间的计算过程叫做卷积或者池化,但是这么表述容易在概念上产生混淆,所以本文不采用这种表述方式,只是拿来作为对比理解使用。
下面对上面的内容做一下总结:
卷积层(C-层或Convolutions层或CONV层或特征提取层,下文统称卷积层):主要作用就是进行特征提取。
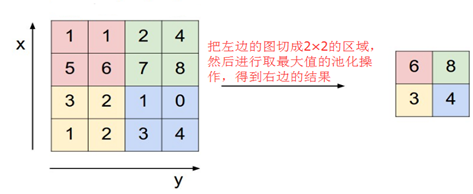
池化层(S-层或子抽样局部平均层或下采样局部平均层或POOL层,下文统称池化层):主要作用是减小特征图,起到降维的作用。常用的方法是选取局部区域的最大值或者平均值。如下图所示:
(图11)
对于第一个卷积层来说(图6的C1-层),一个特征对应一个通道(或叫feature map或特征映射或者叫滤波器,下文统称特征映射),例如三原色(RGB)的图像就需要三个特征映射层。但是经过第一个池化层(图6的S2-层,PS:图中错标成了S1-层)之后,下一个特征提取层
(图6的C3-层)的特征映射 (feature map)个数并不一定与开始的相同了(图6中从8特征变成了20特征),一般情况下会比初始的特征映射个数多,因为根据视觉系统原理----底层的结构构成上层更抽象的结构,所以当前层的特征映射是上一层的特征映射的组合,也就是一个特征映射会对应上一层的一个或多个特征映射。
2.2 接受域和步长
2.2.1 接受域
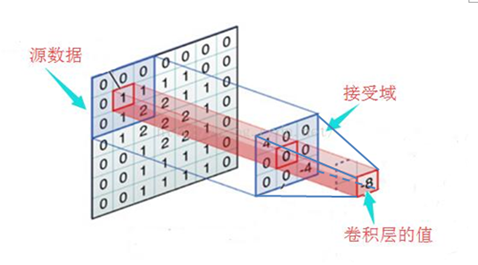
(图12)
如图所示,中间的正方形都表示接受域,其大小为5*5。这里再重复一下:权重(卷积核)指的是数字,接受域指的是权重(卷积核)的大小。
2.2.2 步长
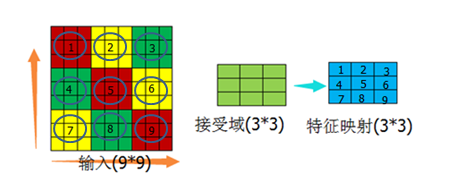
(图13)
接受域的对应范围从输入的区域1移到区域2的过程,或者从区域3移动到区域4都涉及到一个参数:步长,即每次移动的幅度。在此例中的步长可以表示成3或
者(3,3),单个3表示横纵坐标方向都移动3个坐标点,如果(3,2)则表示横向移动3个坐标点,纵向移动2个坐标点。每次移动是按一个方向移动,不是两个方向都移
动(图13中,从区域1移动到区域2、区域3,然后才移动到区域4,如果两个方向都移动三个坐标点则从区域1到了区域5,是不对的)。
2.3卷积神经网络
2.3.1卷积神经网络定义
卷积神经网络是一个多层的神经网络,每层由多个二维平面(特征映射)组成,而每个平面由多个独立神经元组成。
2.3.2卷积神经网络特点
卷积神经网络是为识别二维形状而特殊设计的一个多层感知器,这种网络结构对二维形状的平移、比例缩放、倾斜或者共他形式的变形具有高度不变性。
卷积神经网络是前馈型网络。
2.3.3 卷积神经网络的形式的约束
2.3.3.1 特征提取
每一个神经元从上一层的局部接受域得到突触输人,因而迫使它提取局部特征。一旦一个特征被提取出来,只要它相对于其他特征的位置被近似地保留下来,它的精确位置就变得没有那么重要了。
下图两个X虽然有点稍微变形,但是还是可以识别出来都是X。
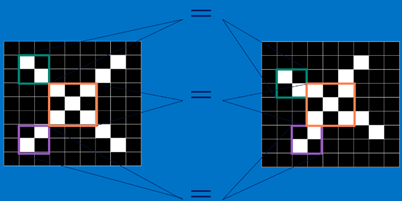
(图14)
2.3.3.2 特征映射
网络的每一个计算层都是由多个特征映射组成的,每个特征映射都是平面形式的。平面中单独的神经元在约束下共享相同的突触权值集(权重),这种结构形式具有如下的有益效果:
a.平移不变性(图14的两个X)
b.自由参数数量的缩减(通过权值共享实现)
这里重点说下共享权值,以及卷积层神经单元个数的确定问题。
以图12的结构为基础,做以下假设:
假设一:输入范围在横纵方向与接受域正好是倍数关系
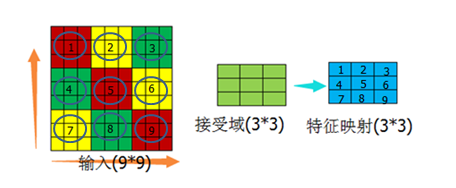
(图15)
先说没有接受域的情况,如果特征映射有9个神经元,这9个神经元与9*9的输入做全连接,那么需要的权重个数为9*9*9=729个。添加了接受域后,9个神经元
分别与接受域做链接,这种情况下如果一个神经元对应一组权重,则有9*9=81个权重值,再假如这一组权重的值是固定的(可参考图12的接受域值,这组值不变,而不是每个值相等),那么就只剩下了9个权重值。从729个权重值减少到9个权重值,这个过程就是权值共享的过程。也许从729减少到9个,差别不是特别大,如果输入是1000*1000,神经元个数是1000万呢?这样的话由权值共享导致的减少的计算量就很客观了。
假设二:输入范围在横纵方向与接受域不是是倍数关系
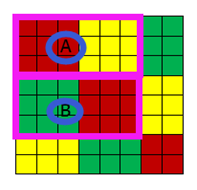
(图16 )
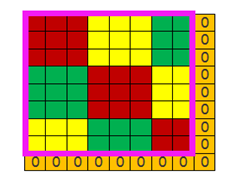
(图17)
以图15为参考,只是把输入域变成图16所示的8*8的情况,若步长还是(3,3),那么横纵向各移动一次后就无法移动了,即接受域的可视范围为粉色边框内的6*6的区域(图16的粉红框A区域和B区域),外侧的2行2列的数据是读不到的。这种情况有两种处理方式,一是直接放弃,但是这种方式几乎不用,另外一种方式在周围补0(图17所示),使输入域变成(3,3)的倍数。
通过上述内容,可以知道每个特征映射的神经元的个数是由输入域大小、接受域、步长共同决定的。如图15,9*9的输入域、3*3的接受域、(3,3)的步长,可
以计算出特征映射的神经元个数为9个。
2.3.3.3 子抽样
每个卷积层后面跟着一个实现局部平均和子抽样的计算层(池化层),由此特征映射的分辨率降低。这种操作具有使特征映射的输出对平移和其他形式的变形
的敏感度下降的作用。
3.用Keras构建一个卷积神经网络
3.1 卷积神经网络结构图
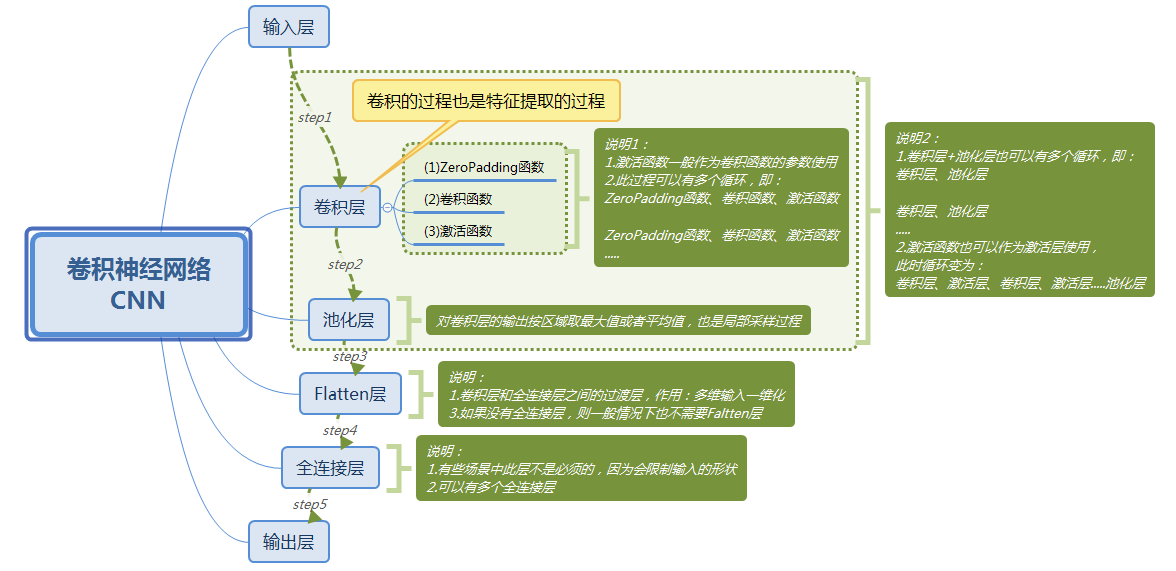
(图18)
3.2 Keras中的输入及权重
3.2.1 示例代码(小数字方便打印验证)
PS:Convolution2D 前最好加ZeroPadding2D,否则需要自己计算输入、kernel_size、strides三者之间的关系,如果不是倍数关系,会直接报错。
| model = Sequential()
model.add(ZeroPadding2D((1, 1), batch_input_shape=(1,
4, 4, 1)))
model.add(Convolution2D (filters=1,kernel_size=(3,3),
strides=(3,3), activation='relu', name='conv1_1'))
model.layers[1].get_weights()
model.add(ZeroPadding2D((1, 1)))
model.add(Convolution2D(filters=1, kernel_size=(2,3),strides=(2,3),
activation='relu', name='conv1_2'))
model.layers[3].get_weights() |
3.2.2 代码解释
1) batch_input_shape=(1, 4, 4, 1)
表示:输入1张1通道(或特征映射)的4*4的数据.因为我采用的是用Tensorflow做后端,所以采用“channels_last”数据格式。
2) filters = 1
表示:有1个通道(或特征映射)
3) kernel_size = (2,3)
表示:权重是2*3的矩阵
4) striders = (2,3)
表示:步长是(2,3)
3.2.3 权重(默认会初始化权重)
3.2.3.1 第一个model.layers[1].get_weights()输出(格式整理后)

(图19)
3.2.3.2 第二个model.layers[1].get_weights()输出
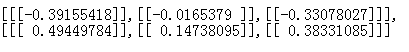
(图20)
3.2.3.3 另外两个输出(没有写的参数值同上)
1)batch_input_shape=(1, 4, 4, 3),filters = 1, kernel_size
= (3,3)

(图21)
2) batch_input_shape=(1, 4, 4, 3),filters = 3, kernel_size
= (2,3)

(图22)
3.2.4 小结
图19到图22的内容是为了说明在Keras中权重的表示方式,为下面的实验做准备。
通过以上参数得出的权重对比,当权重是二维矩阵(n*n)时:
1) [[[…]]]:表示横轴数目
2) [[…]]:表示纵轴数目
3) […]:表示通道的个数。图21和图22的区别:因为图22是3通道3filter,所以每个通道对应一个filter(图20),而图22相当于把3个图20合一起了。
4) […]内逗号隔开的数:filter的个数
5) [[[[…]]]]:这个可能代表层数(前面几个参数是平面的,这个参数是立体的。在下面的实验中没有得到具体验证,只是根据最外层是5个方括号推测的)
3.3 sobel算子转化成权重
由3.2.4的结论,可以把图4的sobel算子转换成Keras中的权重:
weights = [[[[[-1]],[[0]],[[1]]],
[[[-2]],[[0]],[[2]]],[[[-1]],[[0]],[[1]]]]]
weights =np.array(weights)
PS:注意最外围是5个方括号
3.4 实验代码
from PIL import
Image
import numpy as np
from keras.models import Sequential
from keras.layers import Convolution2D, ZeroPadding2D,
MaxPooling2D
from keras.optimizers import SGD
'''
第一步:读取图片数据
说明:这个过程需要安装pillow模块:pip install pillow
'''
##1张1通道的256*256的灰度图片
##data[0,0,0,0]:表示第一张图片的第一个通道的坐标为(0,0)的像素值
img_width, img_height = 256, 256
data = np.empty((1,1,img_width,img_height),dtype="float32")
##打开图片
img = Image.open("D:\\keras\\lena.jpg")
##把图片转换成数组形式
arr = np.asarray(img,dtype="float32")
data[0,:,:,:] = arr
'''
第二步:设置权重
说明:注意最外围是5个方括号
'''
weights = [[[[[-1]],[[0]],[[1]]],[[[-2]],[[0]],[[2]]],[[[-1]],[[0]],[[1]]]]]
weights =np.array(weights)
'''
第三步:组织卷积神经网络
说明:
1.因为实验采用的是默认的tensorflow后端,而输入图像是channels_first模式,所以注意data_format参数的设置
2.为了实验的效果,所以strides、pool_size等参数设置成了1
'''
##第一次卷积
model = Sequential()
model.add(ZeroPadding2D(padding=(2, 2), data_format='channels_first',
batch_input_shape=(1, 1,img_width, img_height)))
model.add(Convolution2D(filters=1,kernel_size=(3,3),strides=(1,1),
activation='relu', name='conv1_1', data_format='channels_first'))
model.set_weights(weights)
##第二次卷积
model.add(ZeroPadding2D((1, 1)))
model.add(Convolution2D (filters=1,kernel_size=(3,3),strides=(1,1),
activation='relu', name='conv1_2',data_format='channels_first'))
model.set_weights(weights)
##池化操作
model.add(ZeroPadding2D((0, 0)))
model.add(MaxPooling2D(pool_size=1, strides=None,data_format='channels_first'))
'''
第四步: 设置优化参数并编译网络
'''
# 优化函数,设定学习率(lr)等参数
sgd = SGD(lr=0.01, decay=1e-6, momentum=0.9,
nesterov=True)
# 使用mse作为loss函数
model.compile(loss='mse', optimizer=sgd, class_mode='categorical')
'''
第五步:预测结果
'''
result = model.predict(data,batch_size=1,verbose=0)
'''
第六步:保存结果到图片
'''
img_new=Image.fromarray(result[0][0]).convert('L')
img_new.save("D:\\keras\\tt123.jpg") |
3.5 实验效果

(图23)

(图24)
图24是池化层参数改为pool_size=2时的效果。
|