| 编辑推荐: |
本文首先介绍这两种方法的区别和联系,然后对分类方法中的逻辑回归进行较详细的说明(包括其基本原理及评估指标),最后结合案例介绍如何利用Python进行逻辑回归分析。
本文来自于csdn,由火龙果软件Anna编辑、推荐。 |
|
前言
回归和分类方法是机器学习中经常用到的方法
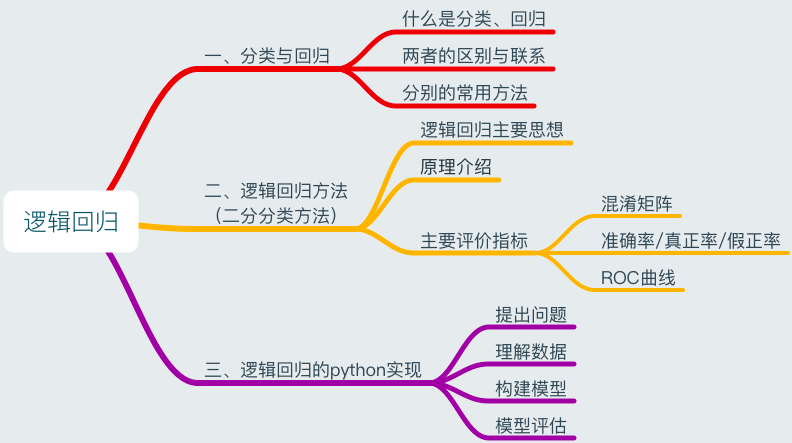
一、分类与回归
1.1什么是分类和回归
区分回归问题和分类问题:
回归问题:输入变量和输出变量均为连续变量的问题;
分类问题:输出变量为有限个离散变量的问题。
因此分类及回归分别为研究这两类问题的方法。
1.2两者区别与联系
区别:从三个维度来对比分类和回归方法:

联系:从prediction角度来看,分类模型和回归模型本质相同,分类模型是将回归模型的输出离散化,比如:
1、Logistic Regression 和 Linear Regression
Linear Regression:输出一个标量wx+b,是连续值,用以处理回归问题;
Logistic Regression:将标量wx+b通过sigmoid函数映射到(0,1)上,并划分一个阈值,大于阈值的分为一类,其他归为另一类,可处理二分分类问题;
对于N分类问题,先得到N组w值不同的wx+b,然后归一化,比如用softmax函数,最后变成N个类上的概率,可处理多分类问题。
2、Support Vector Regression 和 Support Vector Machine
SVR:输出wx+b,即某个样本点到分类面的距离,是连续值,用以处理回归问题;
SVM:将该距离通过sign(·)函数映射,距离为正的样本点为一类,为负的是另一类,故为分类问题。
1.3相应有哪些常用方法
常见的分类方法:
逻辑回归、决策树分类、KNN(K-近邻)分类、贝叶斯分类、人工神经网络、支持向量机(SVM)等
常见的回归方法:
线性回归、多项式回归、逐步回归等
(常见的聚类方法:K-Means(K均值)聚类等)
二、逻辑回归分析
2.1逻辑回归
Logistic回归主要思想是,根据现有数据对决策边界建立回归方程,然后将回归方程映射到分类函数上实现分类。
2.2原理介绍
Logistic回归的原理可以理解为以下四步:
1、利用回归方程表示决策边界
分类问题的目的是找到决策边界,因此我们需要找到一个回归方程来表示这个决策边界: g(W,X)=W^X
,其中 W 代表权重向量。
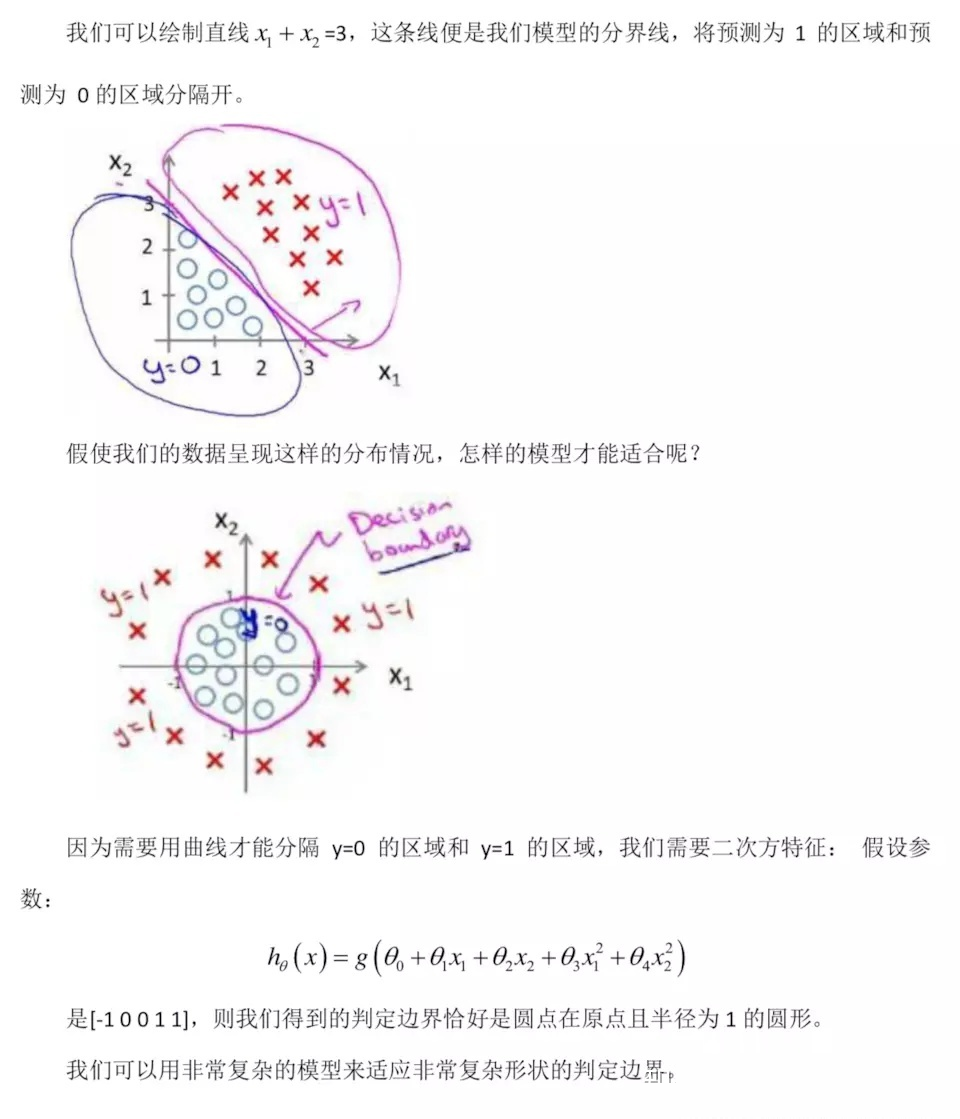
2、利用 Sigmoid 函数对回归关系进行映射
在面对二分分类问题时,可以用1和0分别代表一种情况,此时利用 Sigmoid
函数:
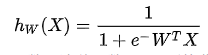
将回归方程的结果映射到分类函数上,即用 Sigmoid 函数表示拟合函数,这种函数是 S 型的非线性函数。
3、在得到拟合函数后,利用损失函数来评价模型与实际值之间的差异大小
损失函数:
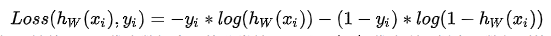
其中 x{i} 代表数据属性值, y{i} 代表数据实际的分类结果, h{W}(x{i}) 代表利用拟合函数得到的预测值,可以用下图表示:
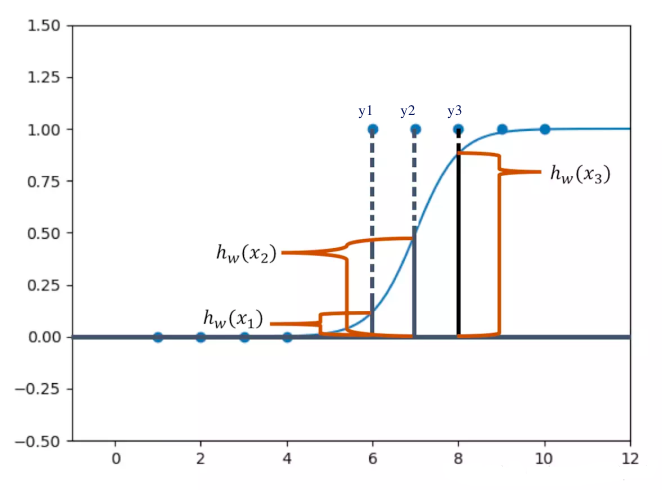
损失函数应满足三个特点,以y{i}=1 时为例:
递减: h{W}(x{i}) 越小,则惩罚力度应越大;
导数绝对值递减:h{W}(x{i}) 越趋近于零,该递减函数的递减幅度也应该越小;
定义域在[0,1]内时,变化幅度应较大。
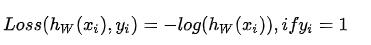
因此利用满足此条件的逻辑函数作为拟合函数。
4、求出损失函数取得极小值时对应的W ,从而得到拟合函数
损失函数求极值利用梯度下降法,本文不做介绍。
2.3评价指标
常见的分类模型性能指标有准确率(precision)、召回率(recall)、ROC曲线等。
1、混淆矩阵(confusion matrix)
包括分类器预测结果:真正TP(true positive)、真负TN(true negative)、假正FP(false
positive)、假负FN(false negative)的数量,其中真正和假负均为正确分类的结果。
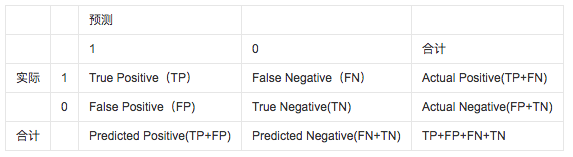
2、准确率、真正率及假正率
预测误差(error,ERR)和准确率(accuracy,ACC)都可以表示误分类样本数量的相关信息,
ACC=1-ERR=TN+TP}/{TN+TP+FN+FP} 。
真正率(TPR)和假正率(FPR)也是很有参考价值的性能指标, TPR={TP}/{AP} 表示预测与实际均为正类别样本数量
与 实际正样本数量的比值, FPR={FP}/{AN} 表示预测为正类别实际为负类别样本数量 与 实际负样本数量的比值。
3、ROC曲线(receiver operator characteristic)
ROC曲线由变量1-Specificity和Sensitivity绘制,其中横轴1-Specificity=假正率(FPR)、纵轴Sensitivity=真正率(TPR),ROC曲线的对角线表示随机猜测,若ROC曲线在对角线下表示分类器性能比随机猜测还差,ROC曲线下的区域面积(area
under the curve,AUC)表示分类模型的性能,反映了模型将正例排在反例前的比例(当AUC=1时,说明将所有正例均排在反例之前)。
原理:
给定 m^{+} 个正例和 n^{-} 个反例,根据学习器预测结果对样例进行排序,然后将分类阈值设置为最大,即所有样例均预测为反例,此时真正例率和假正例率均为0,即在坐标(0,0)处标记一个点。
然后,将分类阈值依次设为每个样例的预测值,即依次将每个样例划分为正例。
设前一个标记点坐标为 (x,y) ,当前若为真正例,则对应标记点坐标为 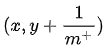
若当前为假正例,则对应标记点坐标为 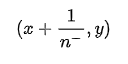
然后用线段连接相邻点即得。
意义:
有助于选择最佳阈值:ROC曲线越靠近左上角,模型查全率越高,最靠近左上角的ROC曲线上的点是分类错误最少的最好阈值,其假正例和假反例总数最少。
可以比较不同学习器的性能:将各个学习器的ROC曲线绘制在同一坐标中,直观比较,越靠近左上角的ROC曲线代表的学习器准确性越高。
AUC同时考虑了学习器对于正例和负例的分类能力,在样本不平衡的情况下,依然能对分类器做出合理评价(如癌症预测)。 
三、逻辑回归的Python实现
利用Python中sklearn包进行逻辑回归分析。
3.1提出问题
根据已有数据探究“学习时长”与“是否通过考试”之间关系,并建立预测模型。
3.2理解数据
1、导入包和数据
#1.导入包
import warnings
import pandas as pd
import numpy as np
from collections import OrderedDict
import matplotlib.pyplot as plt
warnings.filterwarnings('ignore')
#2.创建数据(学习时间与是否通过考试)
dataDict={'学习时间':list(np.arange(0.50,5.50,0.25)),
'考试成绩':[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1,
1, 1, 1, 1, 1, 1, 1]}
dataOrDict=OrderedDict(dataDict)
dataDf=pd.DataFrame(dataOrDict)
dataDf.head()
>>>
学习时间 考试成绩
0 0.50 0
1 0.75 0
2 1.00 0
3 1.25 0
4 1.50 0 |
2、查看数据
#查看数据具体形式
dataDf.head()
#查看数据类型及缺失情况
dataDf.info()
>>>
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20 entries, 0 to 19
Data columns (total 2 columns):
学习时间 20 non-null float64
考试成绩 20 non-null int64
dtypes: float64(1), int64(1)
memory usage: 400.0 bytes
#查看描述性统计信息
dataDf.describe()
>>>
学习时间 考试成绩
count 20.00000 20.000000
mean 2.87500 0.500000
std 1.47902 0.512989
min 0.50000 0.000000
25% 1.68750 0.000000
50% 2.87500 0.500000
75% 4.06250 1.000000
max 5.25000 1.000000
|
3、绘制散点图查看数据分布情况
#提取特征和标签
exam_X=dataDf['学习时间']
exam_y=dataDf['考试成绩']
#绘制散点图
plt.scatter(exam_X,exam_y,color='b',label='考试数据')
plt.legend(loc=2)
plt.xlabel('学习时间')
plt.ylabel('考试成绩')
plt.show() |
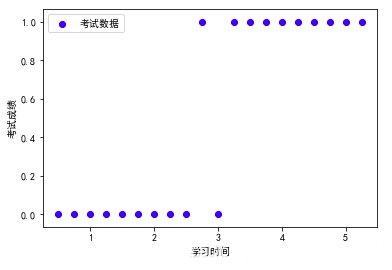
从图中可以看出当学习时间高于某一阈值时,一般都能够通过考试,因此我们利用逻辑回归方法建立模型。
3.3构建模型
1、拆分训练集并利用散点图观察
#1.拆分训练集和测试集
from sklearn.cross_validation import train_test_split
exam_X =exam_X.values.reshape(-1,1)
exam_y =exam_y.values.reshape(-1,1)
train_X,test_X,train_y,test_y =train_test_split (exam_X,exam_y,train_size=0.8)
print ('训练集数据大小为', train_X.size,train_y.size)
print ('测试集数据大小为', test_X.size,test_y.size)
>>>
训练集数据大小为 16 16
测试集数据大小为 4 4
#2.散点图观察
plt.scatter (train_X,train_y, color='b', label='train
data')
plt.scatter (test_X,test_y, color='r', label='test
data')
#plt.plot (test_X,pred_y,color='r')
plt.legend(loc=2)
plt.xlabel('Hours')
plt.ylabel('Scores')
plt.show() |
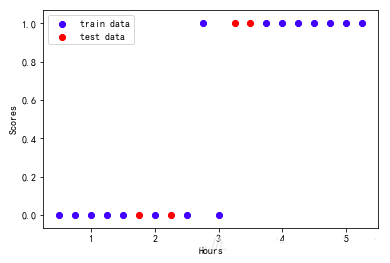
2、导入模型
#3.导入模型
from sklearn.linear_model import LogisticRegression
modelLR=LogisticRegression()
|
3、训练模型
#4.训练模型
modelLR.fit(train_X,train_y) |
3.4模型评估
1、模型评分(即准确率)
| modelLR.score(test_X,test_y)
>>>
0.75 |
2、指定某个点的预测情况
#学习时间确定时,预测为0和1的概率分别为多少?
| #学习时间确定时,预测为0和1的概率分别为多少?
modelLR.predict_proba(3)
>>>
array([[0.36720478, 0.63279522]])
#学习时间确定时,预测能否通过考试?
modelLR.predict(3)
>>>
array([1]) |
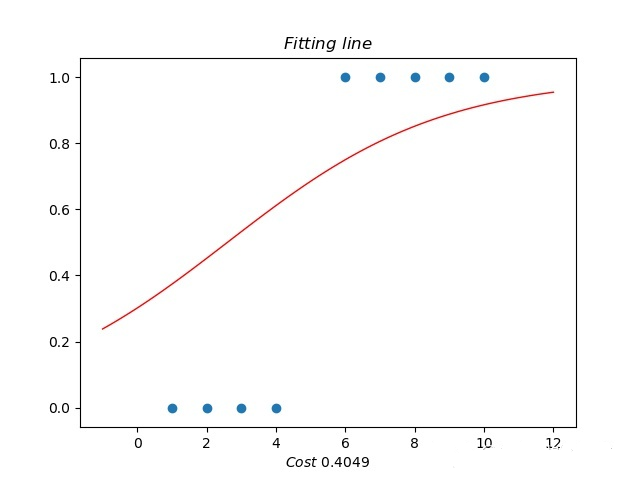
3、求出逻辑回归函数并绘制曲线
逻辑回归函数
| #先求出回归函数y=a+bx,再代入逻辑函数中pred_y=1/(1+np.exp(-y))
b=modelLR.coef_
a=modelLR.intercept_
print('该模型对应的回归函数为:1/(1+exp-(%f+%f*x))'%(a,b))
>>>
该模型对应的回归函数为:1/(1+exp-(-1.527106+0.690444*x))
|
逻辑回归曲线
| #画出相应的逻辑回归曲线
plt.scatter (train_X,train_y,color='b', label='train
data')
plt.scatter (test_X,test_y,color='r', label='test
data')
plt.plot (test_X,1/ (1+np.exp(-(a+b*test_X))),color='r')
plt.plot (exam_X,1/ (1+np.exp(-(a+b*exam_X))),color='y')
plt.legend(loc=2)
plt.xlabel('Hours')
plt.ylabel('Scores')
plt.show() |
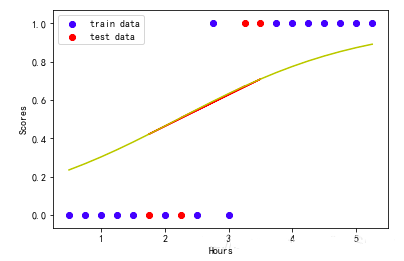
4、得到模型混淆矩阵
| from sklearn.metrics
import confusion_matrix
#数值处理
pred_y=1/(1+np.exp(-(a+b*test_X)))
pred_y=pd.DataFrame(pred_y)
pred_y=round(pred_y,0).astype(int)
#混淆矩阵
confusion_matrix(test_y.astype(str),pred_y.astype(str))
>>>
array([[1, 1],
[0, 2]]) |
从混淆矩阵可以看出:
该模型的准确率ACC为0.75;
真正率TPR和假正率FPR分别为0.50和0.00,说明该模型对负例的甄别能力更强(如果数据量更多,该指标更有说服性,而本案例中数据较少,因此受随机影响较大)。
5、绘制模型ROC曲线
| from sklearn.metrics
import roc_curve, auc ###计算roc和auc
# Compute ROC curve and ROC area for each class
fpr,tpr,threshold = roc_curve(test_y, pred_y)
###计算真正率和假正率
roc_auc = auc(fpr,tpr) ###计算auc的值
plt.figure()
lw = 2
plt.figure(figsize=(10,10))
plt.plot(fpr, tpr, color='r',
lw=lw, label='ROC curve (area = %0.2f)' % roc_auc)
###假正率为横坐标,真正率为纵坐标做曲线
plt.plot([0, 1], [0, 1], color='navy', lw=lw,
linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel ('False Positive Rate')
plt.ylabel ('True Positive Rate')
plt.title('Receiver operating characteristic
example')
plt.legend (loc="lower right")
plt.show() |
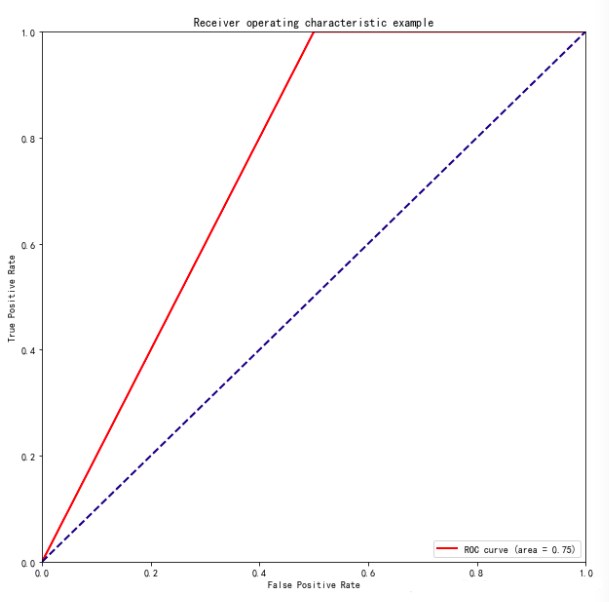
红线以下部分面积等于0.75,与模型准确率一致
红线以下部分面积等于0.75,即误将一个反例划分为正例。
四、总结
理解回归与分类的关系:两者既有区别(三个维度理解),又有联系(将回归方程映射到分类函数);
逻辑回归的参数及其含义:准确率(ACC:模型预测准确度)、真正率(TPR:模型将正例分类正确的能力)、假正率(FPR:模型将负例分类正确的能力)、ROC曲线(可以反映模型正确识别正/负例的能力,也可利用AUC反映模型准确度) |