| 编辑推荐: |
本文主要讲解了人工智能和深度学习概论、图像基础、深度学习基础、深度学习的基本数学、理解的人工神经网络。
本文来自于云+社区,由火龙果软件Anna编辑、推荐。 |
|
人工智能和深度学习概论
AI与ML与DL
Artificial intelligence(人工智能)
使人类通常执行的智力任务自动化的努力
Machine Learning(机器学习)
使系统无需进行显式编程即可自动从数据进行改进
Deep Learning(深度学习)
机器学习的特定子领域
侧重于学习越来越有意义的表示形式的连续层
人工神经网络
最初于1950年代进行调查,始于1980年代
不是真正的大脑模型
受到神经生物学研究的宽松启发
深度学习的深度如何?
深度学习是人工神经网络的重塑,具有两层以上
“深入”并不是指通过这种方法获得的更深刻的理解
它代表连续表示层的想法
深度学习框架
我们的深度学习技术堆栈

GPU和CUDA
GPU(Graphics Processing Unit):
数百个更简单的内核
数千个并发的硬件线程
最大化浮点吞吐量
CUDA(Compute Unified Device Architecture)
并行编程模型,可通过利用GPU显着提高计算性能
cuDNN(CUDA深度神经网络库)
GPU加速的神经网络原语库
它为以下方面提供了高度优化的实现:卷积,池化,规范化和激活层
设置深度学习环境
安装Anaconda3-5.2.0
安装DL框架
$ conda install -c conda-forge tensorflow
$ conda install -c conda-forge keras
启动Jupyter Server
$ jupyter notebook
图像处理基础
像素
像素是图像的原始构建块。 每个图像都包含一组像素
像素被认为是在图像中给定位置出现的光的“颜色”或“强度”
图片的分辨率为1024x768,即1024像素
宽768像素高
灰度与颜色
在灰度图像中,每个像素的标量值为0到255之间,其中零对应于黑色,而255为白色。 0到255之间的值是变化的灰色阴影
RGB颜色空间中的像素由三个值的列表表示:红色代表一个值,绿色代表一个值,蓝色代表另一个值
通过执行均值减法或缩放对输入图像进行预处理,这是将图像转换为浮点数据类型所必需的
图像表示
我们可以将RGB图像概念化,该图像由宽度W和高度H的三个独立矩阵组成,每个RGB分量一个
RGB图像中的给定像素是[0; 255]范围内的三个整数的列表:红色代表一个值,绿色代表第二个值,蓝色代表最终值
RGB图像可以以形状(高度,宽度,深度)存储在3D NumPy多维数组中。
图像分类
图像分类是从一组预定义的类别中为图像分配标签的任务
假设计算机看到的只是一个很大的像素矩阵,那么如何以计算机可以理解的过程来表示图像
应用特征提取以获取输入图像,应用算法并获得量化内容的特征向量
我们的目标是应用深度学习算法来发现图像集合中的潜在模式,从而使我们能够正确分类算法尚未遇到的图像
深度学习基础
数据处理
向量化
将原始数据转换为张量
正常化
所有特征值均在同一范围内,标准偏差为1,平均值为0
特征工程
通过在建模之前将人类知识应用于数据来使算法更好地工作
什么是模型
在训练数据集上训练ML算法时生成的函数
例如。 找出w和b的值,因此f(x)= wx + b紧密匹配数据点。
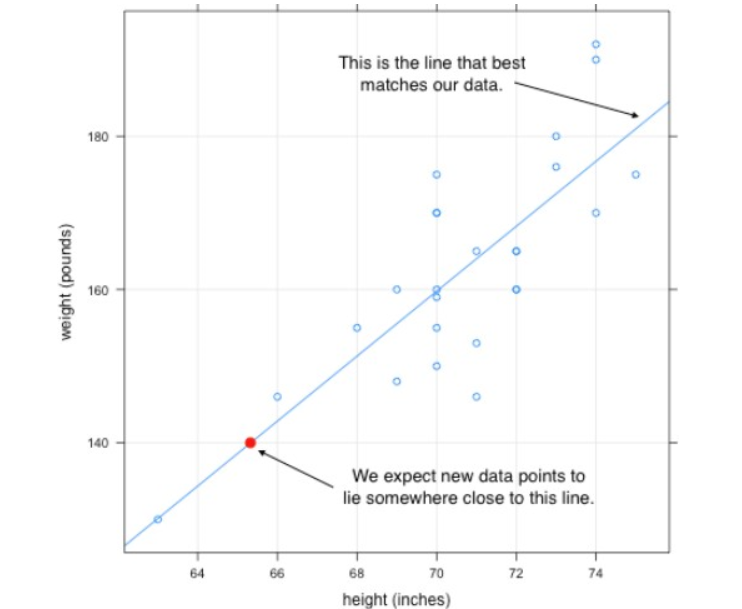
模型重量
模型权重=参数=内核
从训练数据中学到的模型的可学习部分
学习开始之前,这些参数的值会随机初始化
然后调整为具有最佳输出的值
模型超参数:
在实际优化模型参数之前手动设置变量
例如 学习率,批量大小,时代等
Optimizer(优化器)
通过动态调整学习率来确定如何更新网络权重
热门优化器:
SGD(随机梯度下降)
RMSProp(均方根传播)
动量Adam(自适应矩估计)
Loss Function(损失函数)
也称为误差函数或成本函数
通过汇总整个数据集的误差并求平均值来量化模型预测与地面真实程度的接近程度
查找权重组合以最小化损失函数
广泛使用的损失函数
交叉熵(对数损失)
均方误差(MSE)
均值绝对误差(MAE)
Weight Updates

学习率
控制我们在损耗梯度方面调整网络权重的程度
系数,用于衡量模型在损失函数中权重的大小
它确定算法的下一步要使用多少梯度。
指标
研究人员使用度量标准来在每个时期后根据验证集判断模型的性能
分类指标
准确性
精确
召回
回归指标:
平均绝对误差
均方误差
深度学习的基本数学
线性代数:矩阵运算
微积分:微分,梯度下降
统计: 概率
Tensors(张量)
张量:
数值数据的容器
多维数组
机器学习的基本数据结构
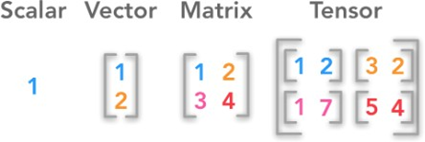
Tensor Operations(张量运算)
Element-wise product
将一个元素的每个元素与另一个元素的每个元素相乘
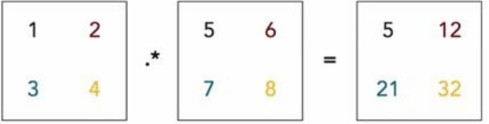
Broadcasting(广播)
广播较小的张量以匹配较大的张量的形状
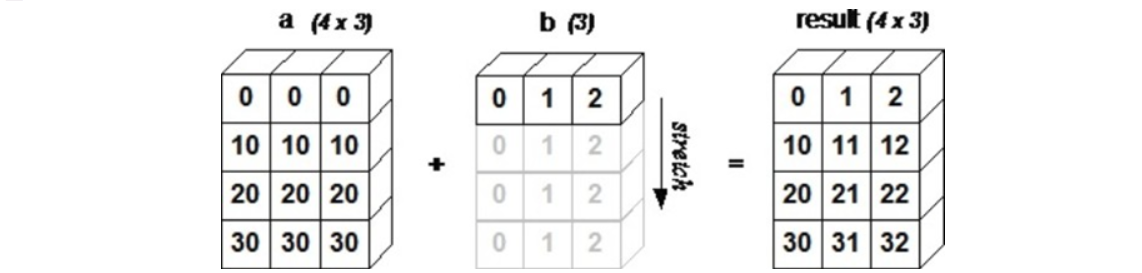
Dot Product Example(点积的例子)
第一个矩阵的列数必须等于第二个矩阵的行数
A(m, n) x B(n, k) = C(m, k)
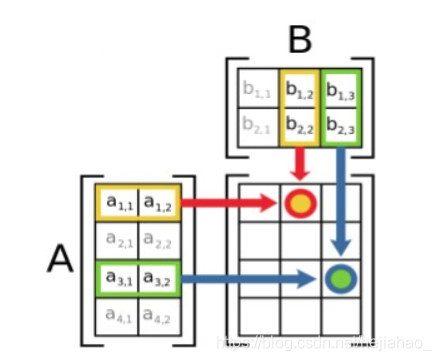
Derivative vs. Gradient (导数与梯度)
导数测量标量值的函数的“变化率”
梯度是张量的导数,导数的多维泛化
在一个变量的函数上定义了导数,而梯度为 用于几个变量的函数。
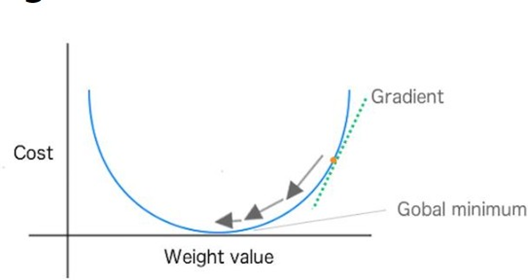
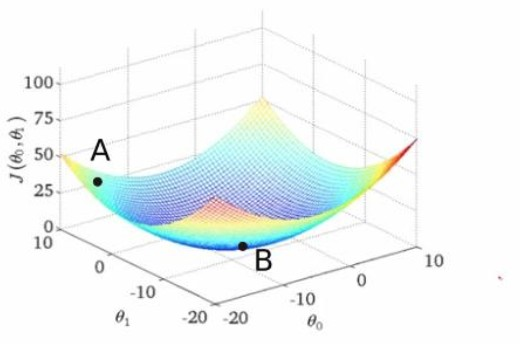
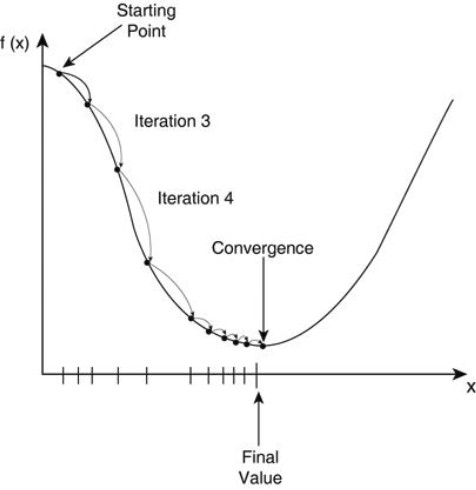
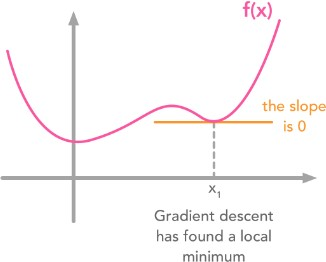
梯度下降
梯度下降法是找到一个函数的局部最小值
成本函数告诉我们离全局最小值有多远
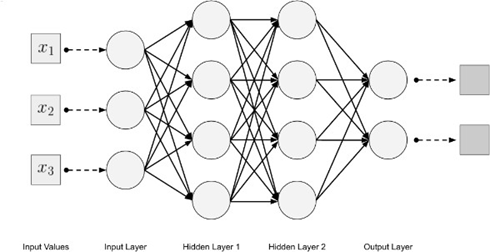
人工神经网络
许多简单的单元在没有集中控制单元的情况下并行工作
ANN由输入/输出层和隐藏层组成
每层中的单元都完全连接到前馈神经网络中相邻层中的所有单元。
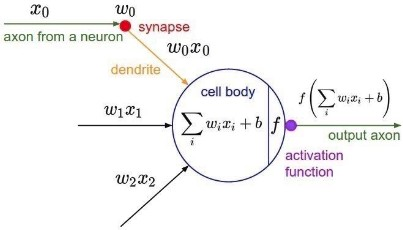
神经元
神经元是人工神经网络的数学功能和基本处理元素
人工神经网络中的每个神经元都会对其所有输入进行加权求和,添加一个恒定的偏差,然后通过非线性激活函数提供结果
层数
一层是一个数据处理模块,使用张量作为输入和输出张量。
隐藏层是网络外部无法观察到的层
大多数层具有权重,而有些则没有权重
每个层具有不同数量的单位
连接权重和偏差
放大输入信号并抑制网络单元噪声的系数。
通过减小某些权重,另一些权重较大,可以使某些功能有意义,并最小化其他功能,从而了解哪些结果有用。
偏差为标量值 输入,以确保无论信号强度如何,每层至少激活几个单位
本质上,ANN旨在优化权重和偏差以最小化误差
Activation Functions(激活函数)
当一个非零值从一个单元传递到另一个单元时,该值被激活
激活功能将输入,权重和偏差的组合从一层转换到下一层
将非线性引入网络的建模功能
流行的Activation Functions
Sigmoid
Tanh
ReLU
Leaky ReLU
Softmax
SoftPlus
案例研究:手写数字分类
LeCun等在1980年代组装的MNIST数据集
70,000个具有28 x 28像素正方形的样本图像
多类分类问题
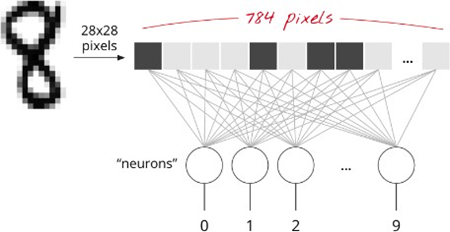
输入层
使用28 x 28 = 784像素作为前馈网络输入层中的输入向量
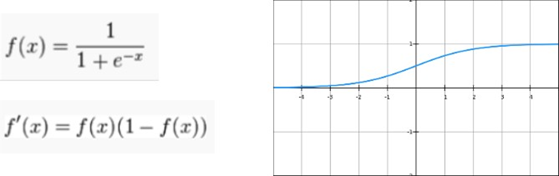
Sigmoid Functions
逻辑函数,可通过将任意值转换为[0,1]来预测输出的可能性
每次梯度信号流过S型门时,其幅值始终最多减少0.25
Softmax Functions
Softmax返回互斥输出类上的概率分布
结果向量清楚地显示了max元素,该元素接近1,并保持顺序
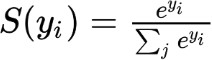
输出层
在输出层上使用Softmax将输出转换为类似概率的值

Classification Loss Function(分类损失函数)
分类交叉熵衡量了多分类模型的性能

在以上示例中,Y’是真实目标,而Y是模型的预测输出。 输出层由Sigmoid激活
SGD, Batch and Epoch
随机梯度下降(SGD),用于计算梯度并更新每个单个训练样本上的权重矩阵
SGD使计算速度更快,而使用整个数据集会使矢量化效率降低。
而不是对整个数据集或单个样本计算梯度, 我们通常在mini-batch(16,32,64)上评估梯度,然后更新权重矩阵
Epoch是所有训练样本的一个前向通过加一个向后通过 |