| 编辑推荐: |
本文主要介绍了一种叫做“感知器”的神经元的组成部分,感知器实现逻辑运算和训练,希望能给大家带来一些帮助。
本文来自于博客园,由火龙果软件Alice编辑、推荐。
|
|
未来将是人工智能和大数据的时代,是各行各业使用人工智能在云上处理大数据的时代,深度学习将是新时代的一大利器,在此我将从零开始记录深度学习的学习历程。
我希望在学习过程中做到以下几点:
了解各种神经网络设计原理。
掌握各种深度学习算法的python编程实现。
运用深度学习解决实际问题。
让我们开始踏上深度度学习的征程。
一、感知器原型
想要了解“神经网络”,我们需要了解一种叫做“感知器”的神经元。感知器在 20 世纪五、六年代由科学家
Frank Rosenblatt 发明,个感知器接受个输,并产个输出。
下图是一个感知器:
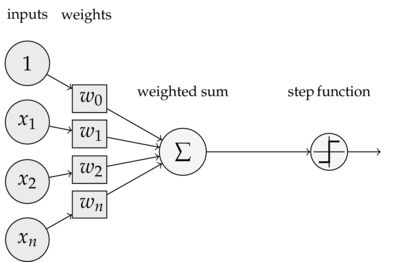
例中的感知器有三个输x1、x2、x3(1*w0作为偏置,后面会讲到)。通常可以有更多或更少输。
Rosenblatt 提议个简单的规则来计算输出。他引权重w1、w2、w3..表相应输对于输出重要性的实数(权重)。神经元的输出为0
或者 1,则由计算权重后的总和 ∑jwjxj 于或者于些阈值决定。和权重样,
阈值是个实数,个神经元的参数。更精确的代数形式:
这就是个感知器所要做的所有事情!
而我们把阖值移动到不等式左边,并用感知器的偏置b=-threshold代替,用偏置而不用阖值。其中实现偏置的一种方法就是如前图所示在输入中引入一个偏置神经元x0=1,则b=x0*w0,那么感知器的规则可以重写.
此时就可以使用阶跃函数来作为感知器的激励函数。
到此我们可以发现,一个感知器由以下几部分组成
输入权值 一个感知器可以接收多个输入
(x1,x2,...,xn∣xi∈R),每个输入上有一个权值wi∈R,此外还有一个偏置项b∈R,就是上图中的w0。
激活函数 感知器的激活函数可以有很多选择在此我们选择下面这个阶跃函数来作为激活函数f:
f(z)={1z>00otherwise
输出 感知器的输出由下面这个公式来计算
y=f(wx+b)公式(1)
接下去我们将会用一个例子来理解感知器的模型。
模型的建立是运用深度学习方法解决问题的基础。
二、感知器的运用
1、感知器实现逻辑运算
我们设计一个感知器,让它来实现and运算。程序员都知道,and是一个二元函数(带有两个参数和),下面是它的真值表:
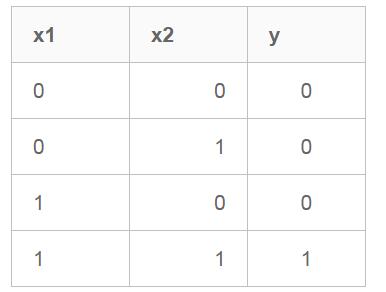
为了计算方便,我们用0表示false,用1表示true。
我们令w1=0.5;w2=0.5;b=0.8,而激活函数f就是前面写出来的阶跃函数,这时,感知器就相当于and函数。我们验算一下:
输入上面真值表的第一行,即,那么根据公式(1),计算输出:
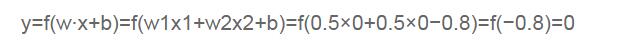
也就是当x1x2都为0的时候,y为0,这就是真值表的第一行。读者可以自行验证上述真值表的第二、三、四行。
可以看到感知器本身是一个线性分类器,它通过求考虑了权重的各输入之和与阖值的大小关系,对事物进行分类。
所以任何线性分类或线性回归问题都可以用感知器来解决。前面的布尔运算可以看作是二分类问题,即给定一个输入,输出0(属于分类0)或1(属于分类1)。
如下面所示,and运算是一个线性分类问题,即可以用一条直线把分类0(false,红叉表示)和分类1(true,绿点表示)分开。
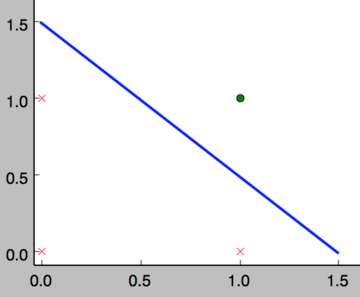
然而,感知器却不能实现异或运算,如下图所示,异或运算不是线性的,你无法用一条直线把分类0和分类1分开。
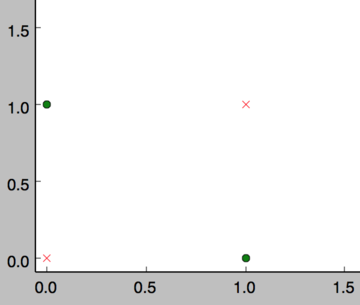
2、感知器的训练
现在,你可能困惑前面的权重项和偏置项的值是如何获得的呢?这就要用到感知器训练算法:将权重项和偏置项初始化为0,然后,利用下面的感知器规则迭代的修改wi和b,直到训练完成。
wib←wi+Δwi←b+Δb
其中:
ΔwiΔb=η(ty)xi=η(ty)
wi是与输入xi对应的权重项,b是偏置项。事实上,可以把b看作是值永远为1的输入所对应的权重w0。t是训练样本的实际值,一般称之为label。而y是感知器的输出值,它是根据公式(1)计算得出。η是一个称为学习速率的常数,其作用是控制每一步调整权的幅度。
每次从训练数据中取出一个样本的输入向量x,使用感知器计算其输出y,再根据上面的规则来调整权重。每处理一个样本就调整一次权重。经过多轮迭代后(即全部的训练数据被反复处理多轮),就可以训练出感知器的权重,使之实现目标函数。
三、python实现感知器
class Perceptron(object):
def __init__(self, input_num, activator):
'''
初始化感知器,设置输入参数的个数,以及激活函数。
激活函数的类型为double -> double
'''
self.activator = activator
# 权重向量初始化为0
self.weights = [0.0 for _ in range(input_num)]
# 偏置项初始化为0
self.bias = 0.0
def __str__(self):
'''
打印学习到的权重、偏置项
'''
return 'weights\t:%s\nbias\t:%f\n' % (self.weights,
self.bias)
def predict(self, input_vec):
'''
输入向量,输出感知器的计算结果
'''
# 把input_vec[x1,x2,x3...]和weights[w1,w2,w3,...]打包在一起
# 变成[(x1,w1),(x2,w2),(x3,w3),...]
# 然后利用map函数计算[x1*w1, x2*w2, x3*w3]
# 最后利用reduce求和
return self.activator(
reduce(lambda a, b: a + b,
map(lambda (x, w): x * w,
zip(input_vec, self.weights))
, 0.0) + self.bias)
def train(self, input_vecs, labels, iteration,
rate):
'''
输入训练数据:一组向量、与每个向量对应的label;以及训练轮数、学习率
'''
for i in range(iteration):
self._one_iteration(input_vecs, labels, rate)
def _one_iteration(self, input_vecs, labels, rate):
'''
一次迭代,把所有的训练数据过一遍
'''
# 把输入和输出打包在一起,成为样本的列表[(input_vec, label), ...]
# 而每个训练样本是(input_vec, label)
samples = zip(input_vecs, labels)
# 对每个样本,按照感知器规则更新权重
for (input_vec, label) in samples:
# 计算感知器在当前权重下的输出
output = self.predict(input_vec)
# 更新权重
self._update_weights(input_vec, output, label,
rate)
def _update_weights(self, input_vec, output, label,
rate):
'''
按照感知器规则更新权重
'''
# 把input_vec[x1,x2,x3,...]和weights[w1,w2,w3,...]打包在一起
# 变成[(x1,w1),(x2,w2),(x3,w3),...]
# 然后利用感知器规则更新权重
delta = label - output
self.weights = map(
lambda (x, w): w + rate * delta * x,
zip(input_vec, self.weights))
# 更新bias
self.bias += rate * delta
def f(x):
'''
定义激活函数f
'''
return 1 if x > 0 else 0
def get_training_dataset():
'''
基于and真值表构建训练数据
'''
# 构建训练数据
# 输入向量列表
input_vecs = [[1,1], [0,0], [1,0], [0,1]]
# 期望的输出列表,注意要与输入一一对应
# [1,1] -> 1, [0,0] -> 0, [1,0] -> 0,
[0,1] -> 0
labels = [1, 0, 0, 0]
return input_vecs, labels
def train_and_perceptron():
'''
使用and真值表训练感知器
'''
# 创建感知器,输入参数个数为2(因为and是二元函数),激活函数为f
p = Perceptron(2, f)
# 训练,迭代10轮, 学习速率为0.1
input_vecs, labels = get_training_dataset()
p.train(input_vecs, labels, 10, 0.1)
#返回训练好的感知器
return p
if __name__ == '__main__':
# 训练and感知器
and_perception = train_and_perceptron()
# 打印训练获得的权重
print and_perception
# 测试
print '1 and 1 = %d' % and_perception.predict([1,
1])
print '0 and 0 = %d' % and_perception.predict([0,
0])
print '1 and 0 = %d' % and_perception.predict([1,
0])
print '0 and 1 = %d' % and_perception.predict([0,
1]) |
|