| 在计算机科学中,树是一种很重要的数据结构,比如我们最为熟悉的二叉查找树(Binary
Search Tree),红黑树(Red-Black Tree)等,通过引入树这种数据结构,我们可以很快地缩小问题规模,实现高效的查找。
在监督学习中,面对样本中复杂多样的特征,选取什么样的策略可以实现较高的学习效率和较好的分类效果一直是科学家们探索的目标。那么,树这种结构到底可以如何用于机器学习中呢?我们先从一个游戏开始。
我们应该都玩过或者听过这么一种游戏:游戏中,出题者写下一个明星的名字,其他人需要猜出这个人是谁。当然,如果游戏规则仅此而已的话,几乎是无法猜出来的,因为问题的规模太大了。为了降低游戏的难度,答题者可以向出题者问问题,而出题者必须准确回答是或者否,答题者依据回答提出下一个问题,如果能够在指定次数内确定谜底,即为胜出。加入了问答规则之后,我们是否有可能猜出谜底呢?我们先实验一下,现在我已经写下了一个影视明星的名字,而你和我的问答记录如下:
是男的吗?Y
是亚洲人吗?Y
是中国人吗?N
是印度人吗?Y
……
虽然只有短短四个问题,但是我们已经把答案的范围大大缩小了,那么接下,第5个问题你应该如何问呢?我相信你应该基本可以锁定答案了,因为我看过的印度电影就那么几部。我们将上面的信息结构化如下图所示:
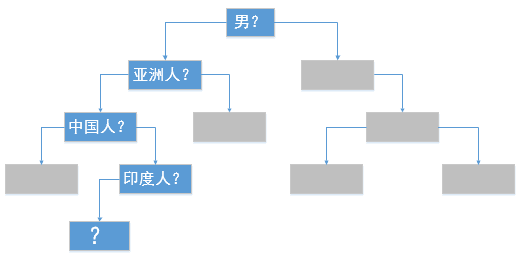
在上面的游戏中,我们针对性的提出问题,每一个问题都可以将我们的答案范围缩小,在提问中和回答者有相同知识背景的前提下,得出答案的难度比我们想象的要小很多。
回到我们最初的问题中,如何将树结构用于机器学习中?结合上面的图,我们可以看出,在每一个节点,依据问题答案,可以将答案划分为左右两个分支,左分支代表的是Yes,右分支代表的是No,虽然为了简化,我们只画出了其中的一条路径,但是也可以明显看出这是一个树形结构,这便是决策树的原型。
1. 决策树算法简介
我们面对的样本通常具有很多个特征,正所谓对事物的判断不能只从一个角度,那如何结合不同的特征呢?决策树算法的思想是,先从一个特征入手,就如同我们上面的游戏中一样,既然无法直接分类,那就先根据一个特征进行分类,虽然分类结果达不到理想效果,但是通过这次分类,我们的问题规模变小了,同时分类后的子集相比原来的样本集更加易于分类了。然后针对上一次分类后的样本子集,重复这个过程。在理想的情况下,经过多层的决策分类,我们将得到完全纯净的子集,也就是每一个子集中的样本都属于同一个分类。
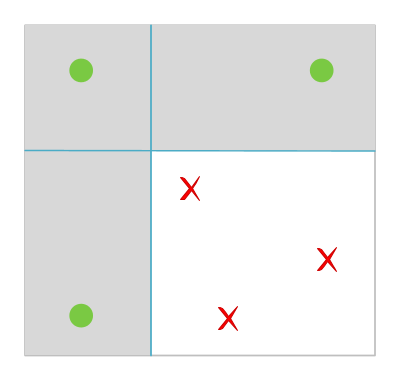
比如上图中,平面坐标中的六个点,我们无法通过其x坐标或者y坐标直接就将两类点分开。采用决策树算法思想:我们先依据y坐标将六个点划分为两个子类(如水平线所示),水平线上面的两个点是同一个分类,但是水平线之下的四个点是不纯净的。但是没关系,我们对这四个点进行再次分类,这次我们以x左边分类(见图中的竖线),通过两层分类,我们实现了对样本点的完全分类。这样,我们的决策树的伪代码实现如下:
| if
y > a:
output dot
else:
if x < b:
output cross
else:
output dot |
由这个分类的过程形成一个树形的判决模型,树的每一个非叶子节点都是一个特征分割点,叶子节点是最终的决策分类。如下图所示
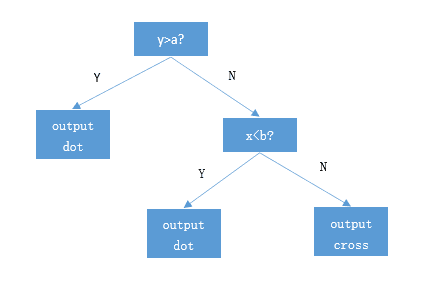
将新样本输入决策树进行判决时,就是将样本在决策树上自顶向下,依据决策树的节点规则进行遍历,最终落入的叶子节点就是该样本所属的分类。
2 决策树算法流程
上面我们介绍决策树算法的思想,可以简单归纳为如下两点:
1.每次选择其中一个特征对样本集进行分类
2.对分类后的子集递归进行步骤1
看起来是不是也太简单了呢?实际上每一个步骤我们还有很多考虑的。在第一个步骤中,我们需要考虑的一个最重要的策略是,选取什么样的特征可以实现最好的分类效果,而所谓的分类效果好坏,必然也需要一个评价的指标。在上文中,我们都用纯净来说明分类效果好,那何为纯净呢?直观来说就是集合中样本所属类别比较集中,最理想的是样本都属于同一个分类。样本集的纯度可以用熵来进行衡量。
在信息论中,熵代表了一个系统的混乱程度,熵越大,说明我们的数据集纯度越低,当我们的数据集都是同一个类别的时候,熵为0,熵的计算公式如下:

其中,P(xi)表示概率,b在此处取2。比如抛硬币的时候,正面的概率就是1/2,反面的概率也是1/2,那么这个过程的熵为:
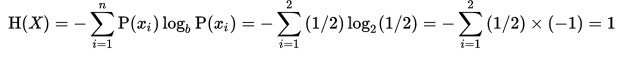
可见,由于抛硬币是一个完全随机事件,其结果正面和反面是等概率的,所以具有很高的熵。假如我们观察的是硬币最终飞行的方向,那么硬币最后往下落的概率是1,往天上飞的概率是0,带入上面的公式中,可以得到这个过程的熵为0,所以,熵越小,结果的可预测性就越强。在决策树的生成过程中,我们的目标就是要划分后的子集中其熵最小,这样后续的的迭代中,就更容易对其进行分类。
既然是递归过程,那么就需要制定递归的停止规则。在两种情况下我们停止进一步对子集进行划分,其一是划分已经达到可以理想效果了,另外一种就是进一步划分收效甚微,不值得再继续了。用专业术语总结终止条件有以下几个:
1.子集的熵达到阈值
2.子集规模够小
3.进一步划分的增益小于阈值
其中,条件3中的增益代表的是一次划分对数据纯度的提升效果,也就是划分以后,熵减少越多,说明增益越大,那么这次划分也就越有价值,增益的计算公式如下:
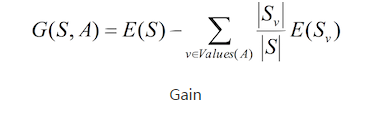
上述公式可以理解为:计算这次划分之后两个子集的熵之和相对划分之前的熵减少了多少,需要注意的是,计算子集的熵之和需要乘上各个子集的权重,权重的计算方法是子集的规模占分割前父集的比重,比如划分前熵为e,划分为子集A和B,大小分别为m和n,熵分别为e1和e2,那么增益就是e
- m/(m + n) * e1 - n/(m + n) * e2。
3. 决策树算法实现
有了上述概念,我们就可以开始开始决策树的训练了,训练过程分为:
1.选取特征,分割样本集
2.计算增益,如果增益够大,将分割后的样本集作为决策树的子节点,否则停止分割
3.递归执行上两步
上述步骤是依照ID3的算法思想(依据信息增益进行特征选取和分裂),除此之外还有C4.5以及CART等决策树算法。
算法框架如下:
|
class DecisionTree(object):
def fit(self, X, y):
# 依据输入样本生成决策树
self.root = self._build_tree(X, y)
def _build_tree(self, X, y, current_depth=0):
#1. 选取最佳分割特征,生成左右节点
#2. 针对左右节点递归生成子树
def predict_value(self, x, tree=None):
# 将输入样本传入决策树中,自顶向下进行判定
# 到达叶子节点即为预测值
|
在上述代码中,实现决策树的关键是递归构造子树的过程,为了实现这个过程,我们需要做好三件事:分别是节点的定义,最佳分割特征的选择,递归生成子树。
3.1 节点定义
决策树的目的是用于分类预测,即各个节点需要选取输入样本的特征,进行规则判定,最终决定样本归属到哪一棵子树,基于这个目的,决策树的每一个节点需要包含以下几个关键信息:
1.判决特征:当前节点针对哪一个特征进行判决
2.判决规则:对于二类问题,这个规则一般是一个布尔表达式
3.左子树:判决为TRUE的样本
4.右子树:判决为FALSE的样本
决策树节点的定义代码如下所示:
|
class DecisionNode():
def __init__(self, feature_i=None, threshold=None,
value=None, true_branch=None, false_branch=None):
self.feature_i = feature_i # 用于测试的特征对应的索引
self.threshold = threshold # 判断规则:>=threshold为true
self.value = value # 如果是叶子节点,用于保存预测结果
self.true_branch = true_branch # 左子树
self.false_branch = false_branch # 右子树
|
3.2 特征选取
特征选取是构造决策树最关键的步骤,其目的是选出能够实现分割结果最纯净的那个特征,其操作流程的代码如下:
| #
遍历样本集中的所有特征,针对每一个特征计算最佳分割点
# 再选取最佳的分割特征
for feature_i in range(n_features):
# 遍历集合中某个特征的所有取值
for threshold in unique_values:
# 以当前特征值作为阈值进行分割
Xy1, Xy2 = divide_on_feature(X_y, feature_i,
threshold)
# 计算分割后的增益
gain = gain(y, y1, y2)
# 记录最佳分割特征,最佳分割阈值
if gain > largest_gain:
largest_gain = gain
best_criteria = {
"feature_i": feature_i,
"threshold": threshold
} |
3.3 节点分裂
节点分裂的时候有两条处理分支,如果增益够大,就分裂为左右子树,如果增益很小,就停止分裂,将这个节点直接作为叶子节点。节点分裂和Gain(分割后增益)的计算可以做一个优化,在上一个步骤中,我们寻找最优分割点的时候其实就可以将最佳分裂子集和Gain计算并保存下来,将上一步中的for循环改写为:
| #
以当前特征值作为阈值进行分割
Xy1, Xy2 = divide_on_feature(X_y, feature_i,
threshold)
# 计算分割后的熵
gain = gain(y, y1, y2)
# 记录最佳分割特征,最佳分割阈值
if gain > largest_gain:
largest_gain = gain
best_criteria = {
"feature_i": feature_i,
"threshold": threshold ,
}
best_sets = {
"left": Xy1,
"right": Xy2,
"gain": gain
} |
为了防止过拟合,需要设置合适的停止条件,比如设置Gain的阈值,如果Gain比较小,就没有必要继续进行分割,所以接下来,我们就可以依据gain来决定分割策略:
| if
best_sets["gain"] > MIN_GAIN:
# 对best_sets["left"]进一步构造子树,并作为父节点的左子树
# 对best_sets["right"]进一步构造子树,并作为父节点的右子树
...
else:
# 直接将父节点作为叶子节点
... |
下面,我们结合一组实验数据来学习决策树的训练方法。实验数据来源于这里,下表中的数据是一组消费调查结果,我们训练决策树的目的,就是构造一个分类算法,使得有新的用户数据时,我们依据训练结果去推断一个用户是否购买这个商品:
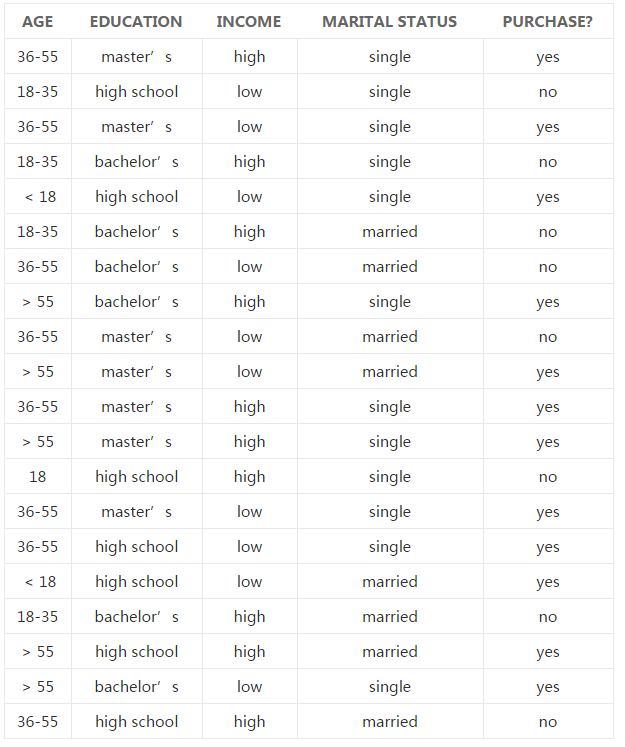
从表中可以看出,我们一共有20组调查样本,每一组样本包含四个特征,分别是年龄段,学历,收入,婚姻状况,而最后一列是所属分类,在这个问题中就代表是否购买了该产品。
监督学习就是在每一个样本都有正确答案的前提下,用算法预测结果,然后根据预测情况的好坏,调整算法参数。在决策树中,预测的过程就是依据各个特征划分样本集,评价预测结果的好坏标准是划分结果的纯度。
为了方便处理,我们对样本数据进行了简化,将年龄特征按照样本的特点,转化为离散的数据,比如小于18对应0,18对应1,18-35对应2,36-55对应3,大于55对应4,以此类推,同样其他的特征也一样最数字化处理,教育水平分别映射为0(hight
school),1(bachelor’s),2(master’s),收入映射为0(low)和1(hight),
婚姻状况同样映射为0(single), 1(married),最终处理后的样本,放到一个numpy矩阵中,如下所示:
| X_y
= np.array(
[[3, 2, 1, 0, 1],
[2, 0, 0, 0, 0],
[3, 2, 0, 0, 1],
[2, 1, 1, 0, 0],
[0, 0, 0, 0, 1],
[2, 1, 1, 1, 0],
[3, 1, 0, 1, 0],
[4, 1, 1, 0, 1],
[3, 2, 0, 1, 0],
[4, 2, 0, 1, 1],
[3, 2, 1, 0, 1],
[4, 2, 1, 0, 1],
[1, 0, 1, 0, 0],
[3, 2, 0, 0, 1],
[3, 0, 0, 0, 1],
[0, 0, 0, 1, 1],
[2, 1, 1, 1, 0],
[4, 0, 1, 1, 1],
[4, 1, 0, 0, 1],
[3, 0, 1, 1, 0]]
) |
4. 新样本预测
依照上面的算法构造决策树,我们将决策树打印出来,如下所示:
| --
Classification Tree --
0 : 4?
T -> 1
F -> 3 : 1?
T -> 0 : 2?
T -> 0
F -> 1
F -> 0 : 3?
T -> 1
F -> 0 : 1?
T -> 0
F -> 1 |
其中,冒号前代表选择的分割特征,冒号后面代表判别规则,二者组合起来就是一个决策树的非叶子节点,每个非叶子节点进一步分割为分为True和False分支,对于叶子节点箭头后面表示最终分类,0表示不购买,1表示购买。由于我们的数据做过简化,所以上述结果不太直观,我们将对应的特征以及判断规则翻译一下:
| 年龄
: 大于55?
是 -> 购买
否 -> 收入 : 高?
是 -> 年龄 : 大于18?
是 -> 不购买
否 -> 购买
否 -> 年龄 : 大于36?
是 -> 购买
否 -> 年龄 : 大于等于18?
是 -> 不购买
否 -> 购买 |
决策树构造完之后,我们就可以用来进行新样本的分类了。决策树的预测过程十分容易理解,只需要将从根节点开始,按照节点定义的规则进行判决,选择对应的子树,并重复这个过程,直到叶子节点即可。决策树的预测功能实现代码如下:
| def
predict_value(self, x, tree=None):
# 如果当前节点是叶子节点,直接输出其值
if tree.value is not None:
return tree.value
# 否则将x按照当前节点的规则进行判决
# 如果判决为true选择左子树,否则选择右子树,
feature_value = x[tree.feature_i]
if feature_value >= tree.threshold:
branch = tree.true_branch
else:
branch = tree.false_branch
# 在选中的子树上递归进行判断
return self.predict_value(x, branch) |
5. 总结
决策树是一种简单常用的分类器,通过训练好的决策树可以实现对未知的数据进行高效分类。从我们的例子中也可以看出,决策树模型具有较好的可读性和描述性,有助于辅助人工分析;此外,决策树的分类效率高,一次构建后可以反复使用,而且每一次预测的计算次数不超过决策树的深度。
当然,决策树也有其缺点。对于连续的特征,比较难以处理,对于多分类问题,计算量和准确率都不理想。此外,在实际应用中,由于其最底层叶子节点是通过父节点中的单一规则生成的,所以通过手动修改样本特征比较容易欺骗分类器,比如在拦击邮件识别系统中,用户可能通过修改某一个关键特征,就可以骗过垃圾邮件识别系统。从实现上来讲,由于树的生成采用的是递归,随着样本规模的增大,计算量以及内存消耗会变得越来越大。
此外,过拟合也是决策树面临的一个问题,完全训练的决策树(未进行剪纸,未限制Gain的阈值)能够100%准确地预测训练样本,因为其是对训练样本的完全拟合,但是,对与训练样本以外的样本,其预测效果可能会不理想,这就是过拟合。解决决策树的过拟合,除了上文说到的通过设置Gain的阈值作为停止条件之外,通常还需要对决策树进行剪枝,常用的剪枝策略有:
Pessimistic Error Pruning:悲观错误剪枝
Minimum Error Pruning:最小误差剪枝
Cost-Complexity Pruning:代价复杂剪枝
Error-Based Pruning:基于错误的剪枝,即对每一个节点,都用一组测试数据集进行测试,如果分裂之后,能够降低错误率,再继续分裂为两棵子树,否则直接作为叶子节点。
Critical Value Pruning:关键值剪枝,这就是上文中提到的设置Gain的阈值作为停止条件。
|