| 编辑推荐: |
| 本文来自于cnblogs,文章主要对CUDA方案下的高并行的计算的详细阐述,同时对其他几种方案进行了描述。 |
|
这个月6号开始,着手解决一个具有实际意义的计算任务。任务数据有9879896条,每条包含30个整数,任务是计算每两条数据之间的斯皮尔相关系数及其P值。原始数据只有500+MB,因此我并不认为这是个多么大的计算任务。随后稍加计算,我还是很惊呆的,要计算(9879896×9879895)÷2≈4.88亿亿组数据,但此时这还只是个数字概念,我也没意识到时间复杂度和空间复杂度的问题。
1. 计算规模初体验
数据格式:9879896行,30列,每列之间以空格符隔开,例如:
0 2 0 2 0 0
0 0 0 0 0 40 0 0 35 0 0 53 0 44 0 0 0 0 0 0 0
0 0 0
0 0 1 148 0 0 0 0 0 0 0 0 0 0 1133 0 1 0 0 1820
0 0 0 2 0 0 0 1 0 0
0 0 0 33 1 0 0 0 0 0 0 0 0 0 231 0 0 0 0 402 0
0 0 0 0 0 0 0 0 0
0 0 6 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 6
0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0
... ...
... ... |
空间复杂度:单纯计算下结果大概有多大吧,每组计算结果包含相关系数和P值,若都以float(占4字节)精度存储,需要占用内存:4.88亿亿×8B≈400TB,当然,我们不具备这么大内存,因此无论以何种方式计算,都需要一批批地重复将数据载入内存、计算、存入硬盘这个过程,直到运算完成。那么,存入硬盘的结果会有400TB吗?不然,P值小于或等于0.05的结果才会需要输出,因此实际上会远远小于这个值,具体会小多少,先运行一批数据后才能做出估算。
时间复杂度:计算的组数规模是(n×(n-1))÷2,那么就看程序能跑多快了。我想先看看MATLAB多线程、Python多线程、Spark分布式计算能跑多快,是否能在最快时间内解决问题。
2. MATLAB多线程
MATLAB写起来最简单,计算相关系数和P值都不用操心,一行自带的函数调用就完成。打开MATLAB左下角的并行池,MATLAB将会自动寻找到机子上有的物理核心,并分配与物理核心数相同的worker。比如我的电脑是4核8线程,它只能开4个worker,不识别虚拟核心。
代码如下:
t1 = clock;
disp('>> loading ...');
A = importdata('D:/MASTER2016/5.CUDA/data-ID-top30-kv3.txt');
b = A'; %由于MATLAB只计算列与列之间的相关系数,因此需要转置操作
disp(etime(clock,t1));
num = size(b, 2);
disp('>> calculating ...');
fid = fopen('D:/MASTER2016/5.CUDA/result-matlab.txt',
'wt');
for i = 1 : num
for j = i+1 : num
[m, n] = corr(b(:, i), b(:, j), 'type', 'Spearman',
'tail', 'both');
if isnan(n) || n>0.05
continue;
end
fprintf(fid, 'X%d\tX%d\t%d\t%d\n', i, j, m, n);
end
end
fclose(fid);
disp('>> OK!'); |
这里我并没有考虑内存空间不够的问题,因为我只是想说明MATLAB的计算速度。开了多颗核心的情况下,MATLAB并没能完全压榨出所有的CPU性能,计算速度缓慢无比,更要命的是,它会越算越慢。据我估算,即使空间复杂度足够,MATLAB也要用超过20年的时间才能算完,这还是不考虑越算越慢的情况。
好了,此方案仅是打酱油。
3. Python多线程
Python语言由于本身的体质问题,Cython下不能调用多核,只能用多线程。理论上是这样,但还是有很多扩展包能够充分压榨出多核CPU性能,例如multiprocessing是其中的佼佼者。multiprocessing用起来也非常简单,考虑到CPU的多核运算下,每颗核心的算力还是很可观的,所有不能把每个计算组都拆成并行线程,那样内存的读写开销反而会使CPU一直在等待状态,不能一直满负载工作。鉴于此,我设计9879895组线程,每组代表某个特定行与剩下的各个数据行形成的数据组。这样每组线程下的运算量还是比较大的,能使CPU尽可能全在满负载状态。
代码如下:
# coding=utf-8
import math
import multiprocessing
import time
import scipy.stats as stats
def calculate2(i, X, all_glb, data_array_glb):
all = all_glb.value
result = []
for j in range(i + 1, all):
x = X
y = data_array_glb[j]
if math.fsum(x) == 0 or math.fsum(y) == 0:
continue
corr, p = stats.spearmanr(x, y)
if p > 0.05:
continue
result.append([i + 1, j + 1, corr, p])
return result
if __name__ == "__main__":
multiprocessing.freeze_support()
input_file = 'D:/MASTER2016/5.CUDA/data-ID-top30-kv3.txt'
output_file = 'D:/MASTER2016/5.CUDA/result-python.txt'
print '>> loading ...'
start = time.clock()
data = open(input_file)
data_array = []
for line in data:
data_array.append(map(int, line.strip().split('
')))
data.close()
print time.clock()-start, 's'
print '>> calculating ...'
results = []
pool_size = 8
pool = multiprocessing.Pool(processes=pool_size)
all = len(data_array)
manager = multiprocessing.Manager()
all_share = manager.Value('i', int(all))
data_array_share = manager.list(data_array)
for i in range(all):
data_X = data_array[i]
results.append(pool.apply_async(calculate2, args=(i,
data_X, all_share, data_array_share)))
pool.close()
pool.join()
print time.clock() - start, 's'
data_array = None
print '>> saving ...'
data2 = open(output_file, 'w')
for res in results:
temp_list = res.get()
for temp in temp_list:
data2.write('X'+str(temp[0])+'\t'+'X'+str(temp[1])
+'\t'+str(temp[2])+'\t'+str(temp[3])+'\n')
print time.clock()-start, 's'
data2.close() |
这里,我依然没有考虑空间复杂度问题,因为要先看看计算能力是否能满足任务要求。Python的这个多线程下,确实能充分榨干CPU性能,风扇呼呼响,要命的是也存在越算越慢的问题。但是,即使CPU一直这么满负载运算,我粗略估算了下,也得要个14年+才能算完,也不算越算越慢的情况。
所以,此方案是打酱油2号。
4. Spark方案
Spark方案我并没有写完,因为写着写着就感觉到。。。肯定还是不行,CPU的算力也就那样了。就算调12台机器一起跑,也不适合用CPU下的线程模型解决问题了。
这种高并行的计算,要想取得最快计算速度,非GPU莫属。
5. CUDA方案
CUDA方案下,首先必须清晰地设计好线程模型,即:我需要用到几块GPU?我需要在每块GPU上设计多少个block?每个block设计多少个线程?每个线程分配多少运算量?这四个问题基本决定了CUDA程序的性能和复杂度。
CUDA是一种异构并行解决方案,即CPU用于控制,GPU用于主运算的方案。一个GPU有一个grid,每个grid里有大量block,每个block里有大量thread。在运算时,每个thread都是完全独立并行地运算,每个线程里的运算靠内核函数控制,这也是CUDA编程的核心,目前只能用CUDA
C编写。因此JCUDA和PyCUDA做的只是内存分配这些CPU端控制的事情,还不能代替GPU端的CUDA
C代码。
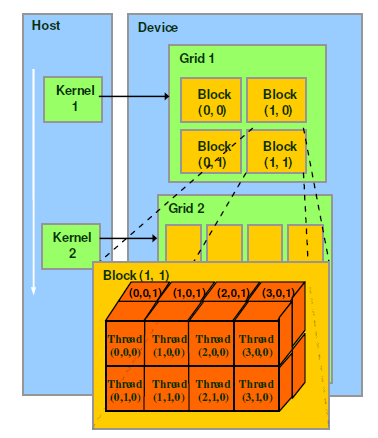
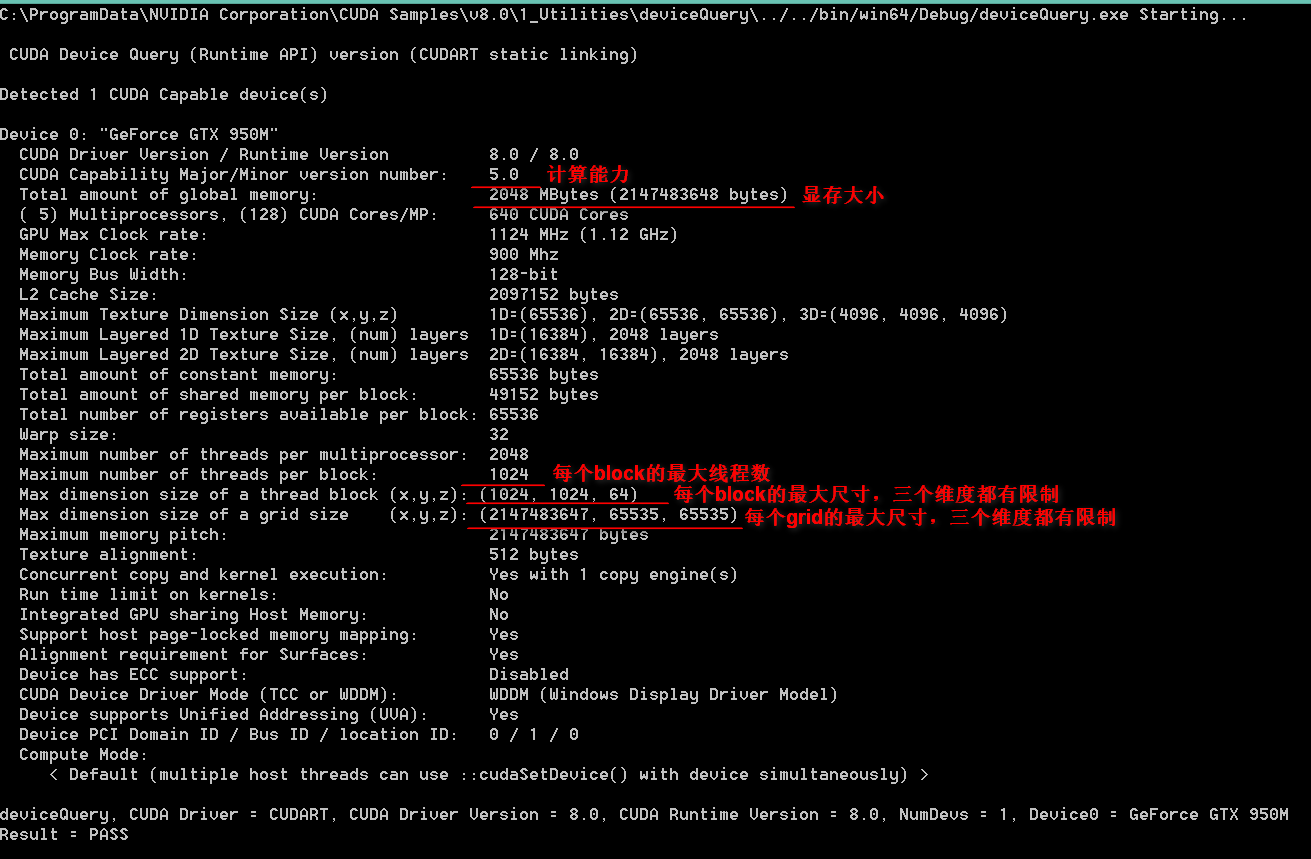
如上图,左边列是Host端,即CPU上执行的控制端,用于分配GPU内存空间,拷贝内存数据到GPU显存等等操作。右边列是Device端,即GPU上的并行模型,由grid,block,thread三者构成。不同型号GPU的最大block数和每个block中的最大thread不同,但是可以查询。在安装好CUDA
Toolkit后,windows用户可以进入C:\ProgramData\NVIDIA Corporation\CUDA
Samples\v8.0\1_Utilities\deviceQuery目录,打开相应版本的项目,执行运行查询。
比如我的机器:
基于此,我设计的线程模型是:比如数据是ROWS行,COLS列,那么有((ROWS-1)×ROWS)÷2组计算,每一行都要与从这行开始后面的每一行进行计算。开辟(ROWS-1)个block,编号0~(ROWS-1)对应着数据的行号。所以,对于第一行,行号是0,要与1~(ROWS-1)的每一行进行计算,一共有(ROWS-1)组,这些计算任务分配给第一块block的1024个线程上计算。依此类推。这样做并不是最佳的任务分配方案,因为不是公平分配,编号越靠后的block分配的任务越少。但是,这样做的好处是便于利用共享内存,加速每一个block内的计算。
比如第一行,将数据第一行存入共享内存,那么它在与其他行分别计算的时候,直接从每个block内的共享内存读取数据,远远比从显存上的全局内存读取速度快得多。需要注意的是,每块block内的共享内存的大小也有硬件限制,上面截图中可以看到,GTX
950M的共享内存是49152B。
Talk is cheap. Show me the code:
#include <time.h>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
// 定义总数据矩阵的行数和列数
#define ROWS 15000
#define COLS 30
// 定义每一块内的线程个数,GT720最多是1024(必须大于总矩阵的列数:30)
#define NUM_THREADS 1024
bool InitCUDA()
{
int count;
cudaGetDeviceCount(&count);
if (count == 0) {
fprintf(stderr, "There is no device.\n");
return false;
}
int i;
for (i = 0; i < count; i++) {
cudaDeviceProp prop;
if (cudaGetDeviceProperties(&prop, i) ==
cudaSuccess) {
if (prop.major >= 1) {
break;
}
}
}
if (i == count) {
fprintf(stderr, "There is no device supporting
CUDA 1.x.\n");
return false;
}
cudaSetDevice(i);
return true;
}
__device__ float meanForRankCUDA(int num)
{
float sum = 0;
for (int i = 0; i <= num; i++) {
sum += i;
}
return sum / (num + 1);
}
__device__ float meanForArrayCUDA(float array[],
int len)
{
float sum = 0;
for (int i = 0; i < len; i++) {
sum += array[i];
}
return sum / len;
}
__device__ float spearmanKernel(int Xarray[],
int Yarray[])
{
//1,对原先的数据进行排序,相同的值取平均值
float Xrank[30];
float Yrank[30];
int col = 30;
for (int i = 0; i < col; i++) {
int bigger = 1;
int equaer = -1;
for (int j = 0; j < col; j++) {
if (Xarray[i] < Xarray[j]) {
bigger = bigger + 1;
}
else if (Xarray[i] == Xarray[j]) {
equaer = equaer + 1;
}
}
Xrank[i] = bigger + meanForRankCUDA(equaer);
}
for (int i = 0; i < col; i++) {
int bigger = 1;
int equaer = -1;
for (int j = 0; j < col; j++) {
if (Yarray[i] < Yarray[j]) {
bigger = bigger + 1;
}
else if (Yarray[i] == Yarray[j]) {
equaer = equaer + 1;
}
}
Yrank[i] = bigger + meanForRankCUDA(equaer);
}
//2,计算斯皮尔曼相关性系数
float numerator = 0;
float denominatorLeft = 0;
float denominatorRight = 0;
float meanXrank = meanForArrayCUDA(Xrank, col);
float meanYrank = meanForArrayCUDA(Yrank, col);
for (int i = 0; i < col; i++) {
numerator += (Xrank[i] - meanXrank) * (Yrank[i]
- meanYrank);
denominatorLeft += powf(Xrank[i] - meanXrank,
2);
denominatorRight += powf(Yrank[i] - meanYrank,
2);
}
float corr = 0;
if ((denominatorLeft != 0) && (denominatorRight
!= 0)) {
corr = numerator / sqrtf(denominatorLeft * denominatorRight);
}
return corr;
}
__global__ static void spearCUDAShared(const
int* a, size_t lda, float* c, size_t ldc, float*
d, size_t ldd)
{
extern __shared__ int data[];
const int tid = threadIdx.x;
const int row = blockIdx.x;
int i, j;
// 同步第1行~倒数第二行到共享内存,行数由block个数(总数据矩阵的行数-1)控制,每个block共享一行数据
if (tid < 30) {
data[tid] = a[row * lda + tid];
}
__syncthreads();
int cal_per_block = gridDim.x - row; // 每个块分担的计算量
int cal_per_thread = cal_per_block / blockDim.x
+ 1; // 每个线程分担的计算量
// 分配各线程计算任务,通过for循环控制在一个线程需要计算的组数
for (i = row + cal_per_thread * tid; i <
(row + cal_per_thread * (tid + 1)) &&
i < gridDim.x; i++) {
int j_row[30]; // 存放总数据矩阵的第j行
for (j = 0; j < 30; j++) {
j_row[j] = a[(i + 1)*lda + j];
}
float corr = spearmanKernel(data, j_row);
c[row * ldc + (i + 1)] = corr;
float t_test = 0;
if (corr != 0) t_test = corr*(sqrtf((30 - 2)
/ (1 - powf(corr, 2))));
d[row * ldd + (i + 1)] = t_test;
//printf("block号:%d, 线程号:%d, 计算组:%d-%d,
id号:%d, block个数:%d, 每块线程个数:%d, 该块总计算量:%d, 该块中每个线程计算量:%d,
corr: %lf, %d, %d, %d - %d, %d, %d\n",
row, tid, row, i + 1, (row*blockDim.x + tid),
gridDim.x, blockDim.x, cal_per_block, cal_per_thread,
corr, data[0], data[1], data[29], j_row[0],
j_row[1], j_row[29]);
}
}
clock_t matmultCUDA(const int* a, float* c,
float* d)
{
int *ac;
float *cc, *dc;
clock_t start, end;
start = clock();
size_t pitch_a, pitch_c, pitch_d;
// 开辟a、c、d在GPU中的内存
cudaMallocPitch((void**)&ac, &pitch_a,
sizeof(int)* COLS, ROWS);
cudaMallocPitch((void**)&cc, &pitch_c,
sizeof(float)* ROWS, ROWS);
cudaMallocPitch((void**)&dc, &pitch_d,
sizeof(float)* ROWS, ROWS);
// 复制a从CPU内存到GPU内存
cudaMemcpy2D(ac, pitch_a, a, sizeof(int)* COLS,
sizeof(int)* COLS, ROWS, cudaMemcpyHostToDevice);
spearCUDAShared << <ROWS - 1, NUM_THREADS,
sizeof(int)* COLS >> > (ac, pitch_a
/ sizeof(int), cc, pitch_c / sizeof(float),
dc, pitch_d / sizeof(float));
cudaMemcpy2D(c, sizeof(float)* ROWS, cc, pitch_c,
sizeof(float)* ROWS, ROWS, cudaMemcpyDeviceToHost);
cudaMemcpy2D(d, sizeof(float)* ROWS, dc, pitch_d,
sizeof(float)* ROWS, ROWS, cudaMemcpyDeviceToHost);
cudaFree(ac);
cudaFree(cc);
end = clock();
return end - start;
}
void print_int_matrix(int* a, int row, int col)
{
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
printf("%d\t", a[i * col + j]);
}
printf("\n");
}
}
void print_float_matrix(float* c, int row, int
col) {
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
printf("%f\t", c[i * col + j]);
}
printf("\n");
}
}
void read_ints(int* a) {
FILE* file = fopen("D:\\MASTER2016\\5.CUDA\\data-ID-top30-kv.txt",
"r");
int i = 0;
int count = 0;
fscanf(file, "%d", &i);
while (!feof(file))
{
a[count] = i;
count++;
if (count == ROWS*COLS) break;
fscanf(file, "%d", &i);
}
fclose(file);
}
int main()
{
int *a; // CPU内存中的总数据矩阵,ROWS行,COLS列
float *c; // CPU内存中的相关系数结果矩阵,ROWS行,ROWS列
float *d; // CPU内存中的T值结果矩阵,ROWS行,ROWS列
a = (int*)malloc(sizeof(int)* COLS * ROWS);
c = (float*)malloc(sizeof(float)* ROWS * ROWS);
d = (float*)malloc(sizeof(float)* ROWS * ROWS);
clock_t start = clock();
printf(">> loading ... rows: %d,
cols: %d", ROWS, COLS);
read_ints(a);
clock_t end = clock() - start;
printf("\nTime used: %.2f s\n", (double)(end)
/ CLOCKS_PER_SEC);
//print_int_matrix(a, ROWS, COLS);
//printf("\n");
printf(">> calculating ... ");
printf("\n---------------------------------------");
printf("\ntotal groups: %lld", (long
long)ROWS*(ROWS - 1) / 2);
printf("\ntotal threads: %d (blocks) *
1024 = %d", (ROWS - 1), (ROWS - 1) * 1024);
printf("\ntotal space complexity: %lld
MB", (long long)((ROWS / 1024) * (ROWS
/ 1024) * 8));
printf("\n---------------------------------------");
if (!InitCUDA()) return 0;
clock_t time = matmultCUDA(a, c, d);
double sec = (double)(time + end) / CLOCKS_PER_SEC;
printf("\nTime used: %.2f s\n", sec);
printf(">> saving ... ");
FILE *f = fopen("D:\\MASTER2016\\5.CUDA\\result-c-2.txt",
"w");
for (int i = 0; i < ROWS; i++) {
for (int j = i + 1; j < ROWS; j++) {
float t_test = d[i * ROWS + j];
if (t_test >= 2.042) {
fprintf(f, "X%d\tX%d\t%f\t%lf\n",
i + 1, j + 1, c[i * ROWS + j], t_test);
}
}
}
fclose(f);
end = clock() - start;
printf("OK\nTime used: %.2f s\n",
(double)(end) / CLOCKS_PER_SEC);
//printf(">> 相关系数结果矩阵: \n");
//print_float_matrix(c, ROWS, ROWS);
//printf(">> T值结果矩阵: \n");
//print_float_matrix(d, ROWS, ROWS);
getchar();
return 0;
}
CUDA第一版 |
需要指出的是,上面程序保存为filename.cu文件,执行nvcc
-o filename filename.cu编译,执行filename即可运行。其中ROWS是从总数据文件中读取的行数,用于控制数据规模调试程序,如果ROWS大于或等于总数据行数,那么就是读取整个文件了。
由于空间复杂度太高,也就是最开始提到的,那么下面做些调整,加个控制参数,每次只计算一定的行数,使显存满载但不超出即可。相应地,内核函数中的索引号,保存文件的函数都需要做些微调,代码如下:
#include <time.h>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
// 定义总数据矩阵的行数和列数
#define ROWS 1000
#define COLS 30
// 控制一次计算占用显存的大小:CONTROL_ROWS*ROWS*8(字节)<
显存
#define CONTROL_ROWS 45
// 定义每一块内的线程个数,GT720最多是1024
#define NUM_THREADS 1024
bool InitCUDA()
{
int count;
cudaGetDeviceCount(&count);
if (count == 0) {
fprintf(stderr, "There is no device.\n");
return false;
}
int i;
for (i = 0; i < count; i++) {
cudaDeviceProp prop;
if (cudaGetDeviceProperties(&prop, i) ==
cudaSuccess) {
if (prop.major >= 1) {
break;
}
}
}
if (i == count) {
fprintf(stderr, "There is no device supporting
CUDA 1.x.\n");
return false;
}
cudaSetDevice(i);
return true;
}
__device__ float meanForRankCUDA(int num)
{
float sum = 0;
for (int i = 0; i <= num; i++) {
sum += i;
}
return sum / (num + 1);
}
__device__ float meanForArrayCUDA(float array[],
int len)
{
float sum = 0;
for (int i = 0; i < len; i++) {
sum += array[i];
}
return sum / len;
}
__device__ float spearmanKernel(int Xarray[],
int Yarray[])
{
//1,对原先的数据进行排序,相同的值取平均值
float Xrank[30];
float Yrank[30];
int col = 30;
for (int i = 0; i < col; i++) {
int bigger = 1;
int equaer = -1;
for (int j = 0; j < col; j++) {
if (Xarray[i] < Xarray[j]) {
bigger = bigger + 1;
}
else if (Xarray[i] == Xarray[j]) {
equaer = equaer + 1;
}
}
Xrank[i] = bigger + meanForRankCUDA(equaer);
}
for (int i = 0; i < col; i++) {
int bigger = 1;
int equaer = -1;
for (int j = 0; j < col; j++) {
if (Yarray[i] < Yarray[j]) {
bigger = bigger + 1;
}
else if (Yarray[i] == Yarray[j]) {
equaer = equaer + 1;
}
}
Yrank[i] = bigger + meanForRankCUDA(equaer);
}
//2,计算斯皮尔曼相关性系数
float numerator = 0;
float denominatorLeft = 0;
float denominatorRight = 0;
float meanXrank = meanForArrayCUDA(Xrank, col);
float meanYrank = meanForArrayCUDA(Yrank, col);
for (int i = 0; i < col; i++) {
numerator += (Xrank[i] - meanXrank) * (Yrank[i]
- meanYrank);
denominatorLeft += powf(Xrank[i] - meanXrank,
2);
denominatorRight += powf(Yrank[i] - meanYrank,
2);
}
float corr = 0;
if ((denominatorLeft != 0) && (denominatorRight
!= 0)) {
corr = numerator / sqrtf(denominatorLeft * denominatorRight);
}
return corr;
}
__global__ static void spearCUDAShared(const
int* a, size_t lda, float* c, size_t ldc, float*
d, size_t ldd, int cols, int start)
{
extern __shared__ int data[];
const int tid = threadIdx.x;
const int row = blockIdx.x;
int i, j;
// 同步第1行~倒数第二行到共享内存,行数由block个数控制,每个block共享一行数据
if (tid < 30) {
data[tid] = a[(start + row) * lda + tid];
}
__syncthreads();
int cal_per_block = cols - (start + row);
// 每个块分担的计算量
int cal_per_thread = cal_per_block / blockDim.x
+ 1; // 每个线程分担的计算量
// 分配各线程计算任务,通过for循环控制在一个线程需要计算的组数
for (i = row + cal_per_thread * tid; i <
(row + cal_per_thread * (tid + 1)) &&
i < cols; i++) {
int j_row[30]; // 存放总数据矩阵的第j行
for (j = 0; j < 30; j++) {
j_row[j] = a[(start + i + 1)*lda + j];
}
float corr = spearmanKernel(data, j_row);
c[row * ldc + (start + i + 1)] = corr;
float t_test = 0;
if (corr != 0) t_test = corr*(sqrtf((30 - 2)
/ (1 - powf(corr, 2))));
d[row * ldd + (start + i + 1)] = t_test;
//printf("block号:%d, 线程号:%d, 计算组:%d-%d,
id号:%d, block个数:%d, 每块线程个数:%d, 该块总计算量:%d, 该块中每个线程计算量:%d,
corr: %lf, %d, %d, %d - %d, %d, %d\n",
row, tid, row, i + 1, (row*blockDim.x + tid),
gridDim.x, blockDim.x, cal_per_block, cal_per_thread,
corr, data[0], data[1], data[29], j_row[0],
j_row[1], j_row[29]);
}
}
clock_t matmultCUDA(const int* a, float* c,
float* d, int start_index, int control_rows)
{
int *ac;
float *cc, *dc;
clock_t start, end;
start = clock();
size_t pitch_a, pitch_c, pitch_d;
// 开辟a、c、d在GPU中的内存
cudaMallocPitch((void**)&ac, &pitch_a,
sizeof(int)* COLS, ROWS);
cudaMallocPitch((void**)&cc, &pitch_c,
sizeof(float)* ROWS, control_rows);
cudaMallocPitch((void**)&dc, &pitch_d,
sizeof(float)* ROWS, control_rows);
// 复制a从CPU内存到GPU内存
cudaMemcpy2D(ac, pitch_a, a, sizeof(int)* COLS,
sizeof(int)* COLS, ROWS, cudaMemcpyHostToDevice);
spearCUDAShared << <control_rows,
NUM_THREADS, sizeof(int)* COLS >> >
(ac, pitch_a / sizeof(int), cc, pitch_c / sizeof(float),
dc, pitch_d / sizeof(float), ROWS - 1, start_index);
cudaMemcpy2D(c, sizeof(float)* ROWS, cc, pitch_c,
sizeof(float)* ROWS, control_rows, cudaMemcpyDeviceToHost);
cudaMemcpy2D(d, sizeof(float)* ROWS, dc, pitch_d,
sizeof(float)* ROWS, control_rows, cudaMemcpyDeviceToHost);
cudaFree(ac);
cudaFree(cc);
cudaFree(dc);
end = clock();
return end - start;
}
void print_int_matrix(int* a, int row, int col)
{
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
printf("%d\t", a[i * col + j]);
}
printf("\n");
}
}
void print_float_matrix(float* c, int row, int
col) {
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
printf("%f\t", c[i * col + j]);
}
printf("\n");
}
}
void read_ints(int* a, char *input_file) {
FILE* file = fopen(input_file, "r");
int i = 0;
int count = 0;
fscanf(file, "%d", &i);
while (!feof(file))
{
a[count] = i;
count++;
if (count == ROWS*COLS) break;
fscanf(file, "%d", &i);
}
fclose(file);
}
void clear_ints(char * out_file) {
FILE *f = fopen(out_file, "w");
fclose(f);
}
void cal_and_save(int i, int *a, char *out_file,
int control_rows) {
float *c; // CPU内存中的相关系数结果矩阵,ROWS行,ROWS列
float *d; // CPU内存中的T值结果矩阵,ROWS行,ROWS列
c = (float*)malloc(sizeof(float)* control_rows
* ROWS);
d = (float*)malloc(sizeof(float)* control_rows
* ROWS);
clock_t time = matmultCUDA(a, c, d, i, control_rows);
FILE *f = fopen(out_file, "a");
for (int m = 0; m < control_rows; m++) {
for (int n = i + m + 1; n < ROWS; n++) {
float t_test = d[m * ROWS + n];
if (t_test >= 2.042) {
fprintf(f, "X%d\tX%d\t%f\t%lf\n",
i + m + 1, n + 1, c[m * ROWS + n], t_test);
}
}
}
fclose(f);
//printf(">> 相关系数结果矩阵: \n");
//print_float_matrix(c, CONTROL_ROWS, ROWS);
//printf(">> T值结果矩阵: \n");
//print_float_matrix(d, CONTROL_ROWS, ROWS);
free(c);
free(d);
}
int main()
{
int *a; // CPU内存中的总数据矩阵,ROWS行,COLS列
a = (int*)malloc(sizeof(int)* COLS * ROWS);
char *input_file = "D:\\MASTER2016\\5.CUDA\\data-ID-top30-kv.txt";
char *out_file = "D:\\MASTER2016\\5.CUDA\\result-c.txt";
clock_t start = clock();
printf(">> loading ... rows: %d,
cols: %d", ROWS, COLS);
read_ints(a, input_file);
clear_ints(out_file);
clock_t end = clock() - start;
printf("\nTime used: %.2f s\n", (double)(end)
/ CLOCKS_PER_SEC);
//print_int_matrix(a, ROWS, COLS);
//printf("\n");
printf(">> calculating ... ");
printf("\n---------------------------------------");
printf("\ntotal groups: %lld", (long
long)ROWS*(ROWS - 1) / 2);
printf("\ntotal threads: %d (blocks) *
1024 = %d", (ROWS - 1), (ROWS - 1) * 1024);
printf("\ntotal space complexity: %lld
MB", (long long)((CONTROL_ROWS / 1024)
* (ROWS / 1024) * 8));
printf("\n---------------------------------------");
if (!InitCUDA()) return 0;
int i;
for (i = 0; i < ROWS - 1; i += CONTROL_ROWS)
{
printf("\n>> calculating and saving
... id: %d ... ", i);
cal_and_save(i, a, out_file, CONTROL_ROWS);
end = clock() - start;
printf("Time used: %.2f s", (double)(end)
/ CLOCKS_PER_SEC);
}
// 不能整除的非整数部分需要计算
//i -= CONTROL_ROWS;
//int control_rows = ROWS - 1 - i;
//printf("\n%d", control_rows);
//if (control_rows > 0) {
// printf("\n>> calculating and saving
... id: %d ... ", i);
// cal_and_save(i, a, out_file, control_rows);
// end = clock() - start;
// printf("Time used: %.2f s", (double)(end)
/ CLOCKS_PER_SEC);
//}
printf("\nFinished.\n");
getchar();
return 0;
}
CUDA第二版 |
到现在,由于空间复杂度过高而显存不够的问题通过增加时间复杂度的方法基本解决了。当然在显存足够的情况下,还是一次性算完是最快的,实测CUDA提速100+倍,数据量越大提速越明显。原因一是你必须被逼着按照CUDA的并行模型来写程序,二是GPU的架构设计确实更适合超大并行程序的加速。游戏画面渲染就是这样,你可以想成一个block控制一块屏幕的渲染,每块block的每个线程控制几个像素格的渲染,而这些图像渲染完全可以是独立并行的,GPU的设计初衷,即是增加核心数,不玩命升频率,增加显存带宽,使成百上千的核心数的并行计算能力得到充分释放。
但是目前的程序当然也不是完美的,我没有考虑如何隐藏内存与显存之间数据的传输延迟,没有考虑多块GPU如何联动运算。后面我会思考这些。
并行计算是计算的未来。异构并行计算,也将是所有架构师必须增加的学习库。
|